Fonction de Tchebychev

La seconde fonction de Tchebychev peut être liée à la première comme suit :

${\displaystyle \psi (x)=\sum _{p\leq x}k\ln p}$

où k est l'unique entier tel que p^k ≤ x et x < p^{k + 1}. Les valeurs de k sont données dans la suite  A206722. Une relation plus directe est donnée par

${\displaystyle \psi (x)=\sum _{n=1}^{\infty }\vartheta \left(x^{\frac {1}{n}}\right).}$

On remarque que la dernière somme a seulement un nombre fini de termes non-nuls :

${\displaystyle \vartheta \left(x^{\frac {1}{n}}\right)=0\quad {\text{pour}}\quad n>\log _{2}x\ ={\frac {\ln x}{\ln 2}}.}$

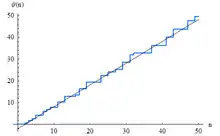
La seconde fonction de Tchebychev est le logarithme du plus petit commun multiple des entiers de 1 à n.

${\displaystyle \operatorname {ppcm} (1,2,\dots ,n)={\rm {e}}^{\psi (n)}.}$

Les valeurs de ppcm(1,2,...,n) pour un entier n sont données par  A003418.

On connait les bornes suivantes pour les fonctions de Tchebychev[1] - [2] (dans ces formules p_k est le k-ème nombre premier : p₁ = 2, p₂ = 3, etc.)

${\displaystyle {\begin{aligned}\vartheta (p_{k})&\geq k\left(\ln k+\ln \ln k-1+{\frac {\ln \ln k-2,050735}{\ln k}}\right)&&{\text{pour }}k\geq 10^{11},\\[8px]\vartheta (p_{k})&\leq k\left(\ln k+\ln \ln k-1+{\frac {\ln \ln k-2}{\ln k}}\right)&&{\text{pour }}k\geq 198,\\[8px]|\vartheta (x)-x|&\leq 0,006788{\frac {x}{\ln x}}&&{\text{pour }}x\geq 10\,544\,111,\\[8px]|\psi (x)-x|&\leq 0,006409{\frac {x}{\ln x}}&&{\text{pour }}x\geq e^{22},\\[8px]0,9999{\sqrt {x}}&<\psi (x)-\vartheta (x)<1,00007{\sqrt {x}}+1,78{\sqrt[{3}]{x}}&&{\text{pour }}x\geq 121.\end{aligned}}}$

De plus, sous l'hypothèse de Riemann,

${\displaystyle {\begin{aligned}|\vartheta (x)-x|&=O\left(x^{{\frac {1}{2}}+\varepsilon }\right)\\|\psi (x)-x|&=O\left(x^{{\frac {1}{2}}+\varepsilon }\right)\end{aligned}}}$

pour tout ε > 0.

Des bornes supérieures existent pour ϑ(x) et ψ(x) telles que[3] - [2]

${\displaystyle {\begin{aligned}\vartheta (x)&<1,000028x\\\psi (x)&<1,03883x\end{aligned}}}$

pour tout x > 0.

Une explication de la constante 1,03883 est donnée par  A206431.

En 1895, Hans Carl Friedrich von Mangoldt a prouvé[4] une expression explicite pour ψ(x) comme une somme sur les zéros non triviaux de la fonction zeta de Riemann :

${\displaystyle \psi _{0}(x)=x-\sum _{\rho }{\frac {x^{\rho }}{\rho }}-{\frac {\zeta '(0)}{\zeta (0)}}-{\tfrac {1}{2}}\ln(1-x^{-2}).}$

(La valeur numérique de ζ′(0)/ζ(0) est ln(2π).) Ici, ρ parcourt les zéros non triviaux de la fonction zêta, et ψ₀ est égale à ψ, sauf en ces points de discontinuités (les puissances premières), où elle prend la valeur moyenne entre les valeurs haute et droite :

${\displaystyle \psi _{0}(x)={\tfrac {1}{2}}\left(\sum _{n\leq x}\Lambda (n)+\sum _{n<x}\Lambda (n)\right)={\begin{cases}\psi (x)-{\tfrac {1}{2}}\Lambda (x)&x=2,3,4,5,7,8,9,11,13,16,\dots \\[5px]\psi (x)&{\mbox{sinon.}}\end{cases}}}$

De la série de Taylor pour le logarithme, le dernier terme dans la formule explicite peut être écrit comme la somme de x^ω/ω sur les zéros triviaux de la fonction zêta, ω = −2, −4, −6, ..., i.e.

${\displaystyle \sum _{k=1}^{\infty }{\frac {x^{-2k}}{-2k}}=-{\tfrac {1}{2}}\ln \left(1-x^{-2}\right).}$

De même, le premier terme, x = x¹/1, correspond au pôle simple de la fonction zêta en 1.

Un théorème d'Erhard Schmidt affirme que, pour une constante positive explicite K, il y a un nombre infini d'entiers naturels x tels que

${\displaystyle \psi (x)-x<-K{\sqrt {x}}}$

et un nombre infini d'entiers naturels x tels que[5] - [6]

${\displaystyle \psi (x)-x>K{\sqrt {x}}.}$

En notation de Landau, on peut l'écrire sous la forme

${\displaystyle \psi (x)-x\neq o\left({\sqrt {x}}\right).}$

Hardy et Littlewood[6] ont trouvé le résultat suivant, plus précis :

${\displaystyle \psi (x)-x\neq o\left({\sqrt {x}}\ln \ln \ln x\right).}$

La première fonction de Tchebychev est le logarithme de la primorielle de x, noté x#:

${\displaystyle \vartheta (x)=\sum _{p\leq x}\ln p=\ln \prod _{p\leq x}p=\ln \left(x\#\right).}$

On prouve ainsi que le primoriel x# est asymptotiquement égal à e^{(1 + o(1))x}, et avec le théorème des nombres premiers, on peut déduire le comportement asymptotique de p_n#.

La fonction de Tchebychev peut être reliée à la fonction de compte des nombres premiers. Si on pose

${\displaystyle \Pi (x)=\sum _{n\leq x}{\frac {\Lambda (n)}{\ln n}}.}$

Alors

${\displaystyle \Pi (x)=\sum _{n\leq x}\Lambda (n)\int _{n}^{x}{\frac {\mathrm {d} t}{t\log ^{2}t}}+{\frac {1}{\ln x}}\sum _{n\leq x}\Lambda (n)=\int _{2}^{x}{\frac {\psi (t)\,\mathrm {d} t}{t\log ^{2}t}}+{\frac {\psi (x)}{\ln x}}.}$

La transition de Π à la fonction de compte, π, est obtenue à l'équation

${\displaystyle \Pi (x)=\pi (x)+{\frac {1}{2}}\pi ({\sqrt {x}})+{\tfrac {1}{3}}\pi \left({\sqrt[{3}]{x}}\right)+\cdots }$

Puisque π(x) ≤ x, pour l'approximation, cette dernière relation peut être réécrite

${\displaystyle \pi (x)=\Pi (x)+O\left({\sqrt {x}}\right).}$

L'hypothèse de Riemann affirme que tous les zéros non triviaux de la fonction zêta ont pour partie réelle 1/2. Dans ce cas, |x^ρ| = √x, et elle peut être décrite par

${\displaystyle \sum _{\rho }{\frac {x^{\rho }}{\rho }}=O\left({\sqrt {x}}\ln ^{2}x\right).}$

De l'égalité, on déduit :

${\displaystyle \pi (x)=\operatorname {li} (x)+O\left({\sqrt {x}}\ln x\right).}$

De bonnes preuves de la véracité de l'hypothèse viennent du fait proposé par Alain Connes et d'autres, que si on différencie la formule de von Mangoldt par rapport à x, on a x = e^u. Par des calculs, on obtient la formule de trace de l'exponentielle de l'opérateur hamiltonien satisfaisant :

${\displaystyle \left.\zeta \left({\tfrac {1}{2}}+{\rm {i}}{\hat {H}}\right)\right|n\geq \zeta \left({\tfrac {1}{2}}+{\rm {i}}E_{n}\right)=0,}$

et

${\displaystyle \sum _{n}{\rm {e}}^{{\rm {i}}uE_{n}}=Z(u)={\rm {e}}^{\frac {u}{2}}-{\rm {e}}^{-{\frac {u}{2}}}{\frac {{\rm {d}}\psi _{0}}{{\rm {d}}u}}-{\frac {{\rm {e}}^{\frac {u}{2}}}{{\rm {e}}^{3u}-{\rm {e}}^{u}}}=\operatorname {Tr} \left({\rm {e}}^{{\rm {i}}u{\hat {H}}}\right),}$

où la somme trigonométrique peut être considérée comme la trace de l'opérateur e^iuĤ (en mécanique statistique), qui n'est vrai que si ρ = 1/2 + iE(n).

Par une approche semi-classique, le potentiel de H = T + V satisfait :

${\displaystyle {\frac {Z(u)u^{\frac {1}{2}}}{\sqrt {\pi }}}\sim \int _{-\infty }^{\infty }{\rm {e}}^{{\rm {i}}\left(uV(x)+{\frac {\pi }{4}}\right)}\,{\rm {d}}x}$

avec Z(u) → 0 si u → ∞.

Des solutions de cette équation intégrale non linéaire peuvent être obtenues (entre autres) par

${\displaystyle V^{-1}(x)\approx {\sqrt {4\pi }}\cdot {\frac {{\rm {d}}^{\frac {1}{2}}}{{\rm {d}}x^{\frac {1}{2}}}}N(x)}$

pour obtenir l'inverse du potentiel:

${\displaystyle \pi N(E)=\operatorname {arg} \xi \left({\tfrac {1}{2}}+{\rm {i}}E\right).}$

La fonction de lissage est définie par

${\displaystyle \psi _{1}(x)=\int _{0}^{x}\psi (t)\,{\rm {d}}t.}$

On peut montrer que

${\displaystyle \psi _{1}(x)\sim {\frac {x^{2}}{2}}.}$

La fonction de Tchebychev en x = e^t minimise la fonctionnelle

${\displaystyle J[f]=\int _{0}^{\infty }{\frac {f(s)\zeta '(s+c)}{\zeta (s+c)(s+c)}}\,{\rm {d}}s-\int _{0}^{\infty }\!\!\!\int _{0}^{\infty }{\rm {e}}^{-st}f(s)f(t)\,{\rm {d}}s\,{\rm {d}}t,}$

ainsi

${\displaystyle f(t)=\psi \left({\rm {e}}^{t}\right){\rm {e}}^{-ct}\quad {\text{pour }}c>0.}$

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Chebyshev function » (voir la liste des auteurs).

• Tom M. Apostol, Introduction to analytic number theory, New York-Heidelberg, Springer-Verlag, coll. « Undergraduate Texts in Mathematics », 1976, 340 p. (ISBN 978-0-387-90163-3, lire en ligne)

• (en) Eric W. Weisstein, « Chebyshev functions », sur MathWorld
• (en) « Mangoldt summatory function », sur PlanetMath
• (en) « Chebyshev functions », sur PlanetMath
• Riemann's Explicit Formula, avec images et animations