Fonction d'influence
La fonction d'influence, ou courbe d'influence, est un outil statistique qui caractérise la sensibilité aux données aberrantes d'une statistique. Introduit par le statisticien Frank Hampel en 1968[1] - [2], il s'agit d'une notion centrale des statistiques robustes.
Définition
Soit une statistique définie en tant que fonctionnelle. Une fonctionnelle est une application qui prend comme argument une distribution de probabilité et donne en image une valeur numérique ou vectorielle. Par exemple, la moyenne peut être définie par la fonctionnelle . La fonction d'influence de la statistique quantifie sa sensibilité asymptotique lorsqu'une proportion infinitésimale des données est corrompue[3].
Définition — Soit une distribution de probabilité, identifiée à sa fonction de répartition, sur un ensemble et un point de . Pour tout , notons la distribution de probabilité sur définie par où est une distribution de Dirac en . est ainsi la distribution d'une variable aléatoire ayant une probabilité d'être égale à et une probabilité d'être distribuée selon .
La fonction d'influence de en évaluée en est définie comme , lorsque cette limite existe.
Si est un estimateur consistant, la fonction d'influence indique le biais asymptotique qu'induit une contamination infinitésimale par une valeur , standardisé par le taux de contamination. Il s'agit donc d'une mesure de la robustesse de la fonctionnelle . Une fonction d'influence bornée par rapport à avec des valeurs proches de indique une fonctionnelle robuste, faiblement influencée par des valeurs aberrantes, tandis qu'une fonction d'influence non bornée, ou avec de grandes valeurs, indique une fonctionnelle non robuste.
Exemples
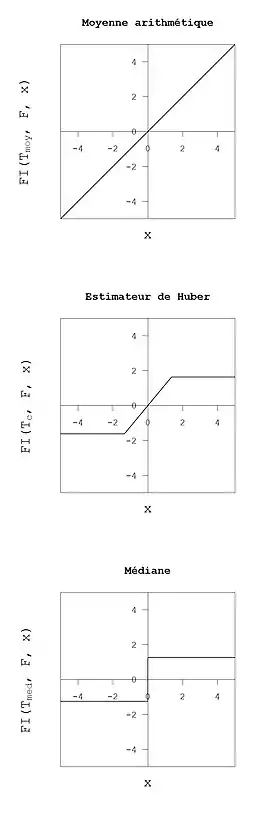
Moyenne arithmétique
La fonctionnelle associée à la moyenne arithmétique est .
Il est aisé de montrer que sa fonction d'influence est :
où est l'espérance de la distribution . Cette fonction n'est pas bornée, la moyenne arithmétique n'est donc pas robuste vis-à-vis des valeurs aberrantes : une seule observation ayant une valeur extrême peut induire un biais arbitrairement grand sur la moyenne.
Médiane
La fonctionnelle définissant la médiane est . Elle a pour fonction d'influence[4] :
où désigne la densité de la distribution , la médiane de et la fonction indicatrice de l'intervalle .
Cette fonction est bornée, et constante par morceaux. Toute contamination par une donnée supérieure (resp. inférieure) à la médiane a le même impact positif (resp.négatif) sur la médiane, quelle que soit sa valeur. Il s'agit donc d'un estimateur robuste. Par comparaison, une contamination de la moyenne par une valeur extrême a un impact plus important que par une donnée proche de la médiane.
Estimateur de Huber
L'estimateur de Huber du centre de observations est défini comme la solution en de l'équation , où et est une constante à fixer par le statisticien. La fonctionnelle associée est donc . La fonction d'influence de cette estimateur est :
où .
Cette fonction d'influence est bornée. Elle présente un compromis entre la robustesse de la médiane (sur laquelle tous les points ont la même influence) et la moyenne (sur laquelle un point à une influence proportionnelle à son écart à l'espérance de la distribution). Un point à une influence proportionnelle à son écart à tant que cet écart reste inférieur à , au-delà tous les points ont une influence valant .
Régression linéaire par les moindres carrés
Considérons un modèle linéaire où est un variable aléatoire réelle, le vecteur des paramètres, une variable aléatoire à valeurs dans dont la première coordonnée vaut (de sorte que comprend une ordonnée à l'origine) et est une variable aléatoire réelle d'espérance nulle.
Étant donné observations , l'estimateur des moindres carrés de est donné par . La fonctionnelle associée à cet estimateur est
où désigne la distribution jointe de et .
La fonction d'influence de cette fonctionnelle est:
Cette fonction d'influence n'est pas bornée. L'estimateur des moindres carrés n'est donc pas robuste contre des données aberrantes. La fonction d'influence est le produit d'une matrice qui ne dépend pas de la contamination , du résidu de la contamination , et de la variable explicative de la contamination . Une donnée a donc un fort impact sur l'estimation si son résidu est élevé ou si sa variable explicative a une valeur extrême [5].
Interprétation en tant que dérivée
La fonction d'influence peut être vue comme une dérivée. Une fonctionnelle est une fonction de l'espace des distributions dans un espace vectoriel généralement réel de dimension fini. Il est souvent possible de développer une fonctionnelle autour d'une distribution donnée en :
Le second terme de l'égalité étant linéaire en , ce développement approxime par une fonction linéaire en de manière analogue à un développement limité d'ordre 1.
Plus formellement, lorsqu'une fonctionnelle est différentiable au sens de Fréchet, la dérivée fonctionnelle de est donnée par .
La fonction d'influence donne aussi le développement de Von Mises d'ordre 1 de la statistique .
Fonction d'influence comme limite de la courbe de sensibilité
La fonction d'influence peut également être introduite comme la limite de la courbe de sensibilité, parfois appelée fonction de sensibilité ou fonction d'influence empirique[6]. Soit un échantillon aléatoire et une statistique. La courbe de sensibilité de la statistique en l'échantillon est définie par :
Cette courbe (lorsque les données sont unidimensionnelles) est généralement représentée en fonction de . Elle mesure l'effet d'une observation additionnelle ayant la valeur sur la statistique .
Le facteur permet d'éviter que la courbe ne tende vers lorsque augmente. En effet, on s'attend à ce que l'effet d'une donnée additionnelle au existantes soit de l'ordre de . On divise donc la différence par ce qui revient à multiplier par .
Supposons les indépendants et identiquement distribués selon une distribution . Si la courbe de sensibilité tend vers une limite simple, presque sûrement, alors cette limite est la fonction d'influence de en :
Cependant, il existe des statistiques dont les courbes de sensibilité n'ont pas de limite. C'est le cas par exemple de la médiane. La fonction d'influence peut quand même exister (la fonction d'influence de la médiane est bien définie), mais elle ne correspond plus à la limite de la courbe de sensibilité.
Notions associées
Sensibilité aux erreurs aberrantes
La sensibilité aux erreurs aberrantes (gross error sensitivity en anglais) d'une statistique en une distribution est définie comme la borne supérieure (éventuellement infinie) de la norme de sa fonction d'influence. Dans le cas univarié, cette sensibilité s'écrit
Dans le cas multivarié, le choix de la norme utilisée à la place de la valeur absolue donne différentes définitions:
- La sensibilité non standardisée, ,
- La sensibilité auto-standardisée, où désigne la variance asymptotique de la statistique ,
- La sensibilité standardisée par l'information de Fisher où désigne l'information de Fisher associée au paramètre , si celle-ci est disponible.
Il s'agit d'un indicateur de la robustesse d'une statistique : plus cette sensibilité est faible, plus la statistique est robuste.
B-robustesse
On dit qu'une statistique ou qu'un estimateur est B-robuste (B est l'initiale de bounded, signifiant borné en anglais) lorsque sa fonction d'influence est bornée, c'est-à-dire lorsque sa sensibilité aux erreurs aberrantes est finie. Intuitivement, cela signifie que cette statistique ne peut pas être "cassée" par une seule observation mal placée. Généralement, les estimateurs classiques ne sont pas B-robustes: moyennes, écart-type, estimateur des moindres carrés, la plupart des estimateurs par maximum de vraisemblance ou par méthode des moments. Plusieurs méthodes introduites par les statistiques robustes existent pour obtenir des estimateurs B-robustes.
Sensibilité aux variations locales
La sensibilité aux variations locales (local shift sensitivity en anglais) donne une indication des variations de la fonction d'influence :
Une fonction d'influence peut être bornée mais avoir une sensibilité aux variations locales finie et vice-versa.
Point de rejet
Le point de rejet d'une statistique en est défini comme le rayon au delà duquel une observation n'a plus aucune influence sur la statistique, Une point de rejet fini signifie que la statistique n'est plus du tout influencée par des observations trop extrêmes. Ce peut être une propriété recherchée de certains estimateurs si l'on suspecte par exemple que des données aberrantes sont issues d'un processus différent des autres et n'apportent aucune information.
Point de rupture
Le point de rupture (breakdown point en anglais) désigne la proportion de contamination suffisant à donner une valeur aberrante à un estimateur. Plus formellement, c'est la proportion minimale de contamination pouvant induire un biais asymptotique arbitrairement grand :
Le point de rupture de la médiane est par exemple de car il faut nécessairement changer la moitié des données pour pouvoir faire prendre à la médiane n'importe quelle valeur aberrante. Le point de rupture de la moyenne en revanche est de car une seule donnée, placée suffisamment loin des autres, permet de donner à la moyenne n'importe quelle valeur.
Le point de rupture n'est pas défini à partir de la fonction d'influence mais il y est lié. En effet, un estimateur ayant un point de rupture non nul est nécessairement B-robuste. La réciproque n'est cependant pas vraie en général, il existe des estimateurs B-robustes ayant un point de rupture nul, même si ceux-ci sont rares.
Propriétés
Espérance de la fonction d'influence
La fonction d'influence est d'espérance nulle lorsque la contamination suit la même loi que les données :
Cette propriété, combinée à l'utilisation de la fonction d'influence comme développement limité permet une approximation intéressante. Considérons un échantillon de variables aléatoires indépendantes et identiquement distribuées suivant une distribution et notons la fonction de répartition empirique de cet échantillon. Alors :
Ce qui permet d'approximer par .
Cela peut être utile pour corriger un éventuel biais de dû à la taille finie de l'échantillon. Cette correction est très proche de celle réalisée par la méthode du jackknife. Pour rendre ce lien plus explicite, on peut remplacer dans l'expression précédente par , ce qui revient à approximer la fonction d'influence par la courbe de sensibilité.
Variance asymptotique
La variance asymptotique d'une statistique est définie comme la limite de lorsque tend vers l'infini. Elle peut être calculée à partir de la fonction d'influence.
Notons un échantillon aléatoire où les sont indépendants et identiquement distribués selon une distribution . Alors, la variance asymptotique de correspond à la variance de sa fonction d'influence :
Fonction d'influence des M-estimateurs
La fonction d'influence d'un M-estimateur se calcule facilement à partir de sa fonction de score. Soit un M-estimateur d'un paramètre . Notons sa fonction de score. Étant donné un échantillon, cet estimateur est donc solution de l'équation .
Alors, si est consistent et vérifie quelques conditions de régularités, la fonction d'influence de est donnée par :
où et où est la vraie valeur du paramètre.
La fonction d'influence d'un estimateur est donc proportionnelle à sa fonction de score. Il s'ensuit qu'un M-estimateur est B-robuste si et seulement si sa fonction de score est bornée. Cela donne une grande importance aux M-estimateurs dans les statistiques robustes. En effet il est facile de construire des estimateur robustes par exemple en tronquant simplement la fonction de score d'estimateurs existants (et en corrigeant le biais induit).
Voir aussi
Références
- Frank R. Hampel, « The Influence Curve and its Role in Robust Estimation », Journal of the American Statistical Association, vol. 69, no 346, , p. 383–393 (ISSN 0162-1459 et 1537-274X, DOI 10.1080/01621459.1974.10482962, lire en ligne)
- (en) Frank R. Hampel, Contributions to the theory of robust estimation : Ph.D. thesis.,
- (en) Frank R. Hampel, Elvezio M. Ronchetti, Peter J. Rousseuw et Werner A. Stahel, Robust Statistics: The Approach Based on Influence Functions, Wiley,
- Christophe Croux, « Limit behavior of the empirical influence function of the median », Statistics & Probability Letters, vol. 37, no 4, , p. 331–340 (ISSN 0167-7152, DOI 10.1016/s0167-7152(97)00135-1, lire en ligne)
- Stephane Heritier, Eva Cantoni, Samuel Copt et Maria-Pia Victoria-Feser, Robust Methods in Biostatistics, Wiley Series in Probability and Statistics, (ISSN 1940-6347, DOI 10.1002/9780470740538, lire en ligne)
- (en) Ricardo A. Maronna, R. Douglas Martin et Victor J. Yohai, Robust statistics : Theory and Methods, Wiley,

![{\displaystyle T:F\mapsto T(F)=\mathbb {E} _{X\sim F}[X]}](https://img.franco.wiki/i/a5f6fbda9546ae45922634c62c150528ea72d126.svg)



![{\displaystyle \varepsilon \in [0,1]}](https://img.franco.wiki/i/d472b1b7207f57be05aaefccd6651d486dd59a8c.svg)








![{\displaystyle T_{moy}:F\mapsto \mathbb {E} _{X\sim F}[X]}](https://img.franco.wiki/i/77d6e8bbe063c5ff80617afe9e27380978869d0f.svg)


























































![{\displaystyle \mathbb {E} _{X\sim F}\left[FI(T,F,X)\right]=0}](https://img.franco.wiki/i/1e3d3211d60ebf54201e79df038bca047fb11a53.svg)














![{\displaystyle M=-\mathbb {E} _{X\sim F}\left[{\frac {\partial }{\partial \theta }}\psi (X,\theta )\right]}](https://img.franco.wiki/i/ba4dc0d95f13ab48371f25191dcdf3504b2d1c1a.svg)