Fonction H de Chandrasekhar

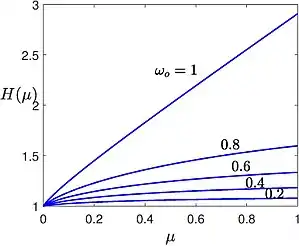
Fonction H pour diverses valeurs de l'albédo.

La fonction introduite par Subrahmanyan Chandrasekhar est généralement définie par l'équation intégrale établie par Viktor Ambartsumian

${\displaystyle H(\mu )=1+\mu H(\mu )\int _{0}^{1}{\frac {\Psi (\mu ')}{\mu +\mu '}}H(\mu ')\,d\mu '}$

où ${\displaystyle \Psi (\mu )}$ est une fonction caractéristique décrivant la diffusion dans le milieu. C'est un polynôme pair satisfaisant

${\displaystyle \int _{0}^{1}\Psi (\mu )\,d\mu \leq {\frac {1}{2}}}$

Le cas correspondant à la limite haute est dit conservatif (il conserve la densité de flux d'énergie).

L'isotropie correspond à

${\displaystyle 2\Psi =\omega _{0}}$

où ${\displaystyle 0\leq \omega _{0}\leq 1}$ est l'albédo, constant. ${\displaystyle \omega _{0}=1}$ correspond au cas de la diffusion pure.

Une définition équivalente plus utilisée pour l'évaluation numérique s'écrit

${\displaystyle {\frac {1}{H(\mu )}}=\left[1-2\int _{0}^{1}\Psi (\mu )\,d\mu \right]^{1/2}+\int _{0}^{1}{\frac {\mu '\Psi (\mu ')}{\mu +\mu '}}H(\mu ')\,d\mu '}$

Dans le cas conservatif le premier terme de l'équation ci-dessus s'annule.

• ${\displaystyle \int _{0}^{1}H(\mu )\Psi (\mu )\,d\mu =1-\left[1-2\int _{0}^{1}\Psi (\mu )\,d\mu \right]^{1/2}}$

Dans le cas conservatif cette équation se réduit à

${\displaystyle \int _{0}^{1}\Psi (\mu )d\mu ={\frac {1}{2}}}$

• ${\displaystyle \left[1-2\int _{0}^{1}\Psi (\mu )\,d\mu \right]^{1/2}\int _{0}^{1}H(\mu )\Psi (\mu )\mu ^{2}\,d\mu +{\frac {1}{2}}\left[\int _{0}^{1}H(\mu )\Psi (\mu )\mu \,d\mu \right]^{2}=\int _{0}^{1}\Psi (\mu )\mu ^{2}\,d\mu }$

Dans le cas conservatif cette équation se réduit à

${\displaystyle \int _{0}^{1}H(\mu )\Psi (\mu )\mu d\mu =\left[2\int _{0}^{1}\Psi (\mu )\mu ^{2}d\mu \right]^{1/2}}$.

• Pour une fonction caractéristique correspondante à la diffusion Thomson ou Rayleigh ${\displaystyle \Psi (\mu )=a+b\mu ^{2}}$ où ${\displaystyle a,b}$ sont deux constantes satisfaisant ${\displaystyle a+b/3\leq 1/2}$ et si on définit le moment d'ordre ${\displaystyle n}$ par ${\displaystyle M_{n}=\int _{0}^{1}H(\mu )\mu ^{n}\,d\mu ,\ n\geq 0}$ alors

${\displaystyle M_{0}=1+{\frac {1}{2}}(aM_{0}^{2}+bM_{1}^{2})}$

et

${\displaystyle (a+b\mu ^{2})\int _{0}^{1}{\frac {H(\mu ')}{\mu +\mu '}}\,d\mu '={\frac {H(\mu )-1}{\mu H(\mu )}}-b(M_{1}-\mu M_{0})}$

En utilisant la variable complexe ${\displaystyle z}$ l'équation de définition de H s'écrit

${\displaystyle H(z)=1-\int _{0}^{1}{\frac {z}{z+\mu }}H(\mu )\Psi (\mu )\,d\mu ,\quad \int _{0}^{1}|\Psi (\mu )|\,d\mu \leq {\frac {1}{2}},\quad \lim \limits _{\delta \to 0}\int _{0}^{\delta }|\Psi (\mu )|\,d\mu =0}$

Dans le plan ${\displaystyle \Re (z)>0}$ la solution est

${\displaystyle \ln H(z)={\frac {1}{2\pi i}}\int _{-i\infty }^{+i\infty }\ln T(w){\frac {z}{w^{2}-z^{2}}}\,dw}$

où la partie imaginaire de ${\displaystyle T(z)}$ s'annule si ${\displaystyle z^{2}}$ est réel, c'est-à-dire si ${\displaystyle z^{2}=u+iv\equiv u}$. On a alors

${\displaystyle T(z)=1-2\int _{0}^{1}\Psi (\mu )\,d\mu -2\int _{0}^{1}{\frac {\mu ^{2}\Psi (\mu )}{u-\mu ^{2}}}\,d\mu }$

Dans le cas conservatif ${\displaystyle 0\leq z\leq 1}$ la solution est unique. Dans le cas contraire ${\displaystyle T(z)=0}$ admet les racines ${\displaystyle \pm {\frac {1}{k}}}$. Il existe donc une solution donnée par

${\displaystyle H_{1}(z)=H(z){\frac {1+kz}{1-kz}}}$

Le développement suivant particulièrement connu car il est à la base de la méthode SN

${\displaystyle H(\mu )={\frac {1}{\mu _{1}\cdots \mu _{n}}}{\frac {\prod _{i=0}^{n}(\mu +\mu _{i})}{\prod _{\alpha }(1+k_{\alpha }\mu )}}}$

où les ${\displaystyle \mu _{i}}$ sont les racines des polynômes de Legendre ${\displaystyle P_{2n}}$ et les ${\displaystyle k_{\alpha }}$ les solutions strictement positives de l'équation caractéristique

${\displaystyle 2\sum _{j=1}^{n}{\frac {a_{j}\Psi (\mu _{j})}{1-k^{2}\mu _{j}^{2}}}}$

Les ${\displaystyle a_{j}}$ sont les poids de la quadrature donnés par

${\displaystyle a_{j}={\frac {1}{P_{2n}'(\mu _{j})}}\int _{-1}^{1}{\frac {P_{2n}(\mu _{j})}{\mu -\mu _{j}}}\,d\mu _{j}}$

D'une façon générale il existe diverses méthode pour le calcul numérique des fonctions H[2] - [3].

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Chandrasekhar's H-function » (voir la liste des auteurs).

• Méthode de Wiener-Hopf
• Problème de Milne

• Code de calcul Matlab accessible sur le site suivant : Mike Simcock, « Chandrasekhar's H function », sur MathWorks