Expérience de Melde
L’expérience de Melde est une expérience scientifique réalisée au XIXe siècle par le physicien allemand Franz Melde sur les ondes stationnaires produites sur une corde tendue reliée à un vibreur électrique.
Historique
Franz Melde, physicien allemand du XIXe siècle connu pour ses travaux en acoustique et sur les mouvements vibratoires, découvrit les ondes stationnaires et les nomma ainsi vers 1860[1] - [2] - [3] - [4]. Cette expérience permit de démontrer que les ondes mécaniques subissent des phénomènes d'interférences. La superposition d'ondes mécaniques progressives voyageant dans des sens opposés forme des points stationnaires sur la corde, appelés nœuds. Ces ondes furent appelées stationnaires par Melde car la position des nœuds et des ventres (points d'amplitude de vibration maximale) demeure la même au cours du temps.
Principe
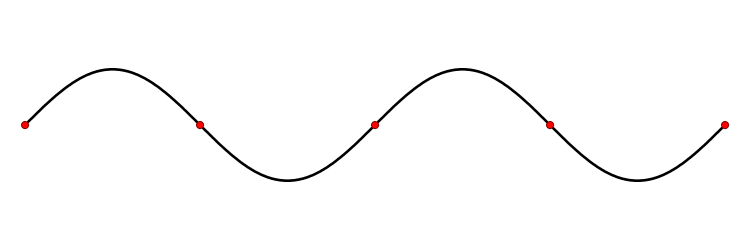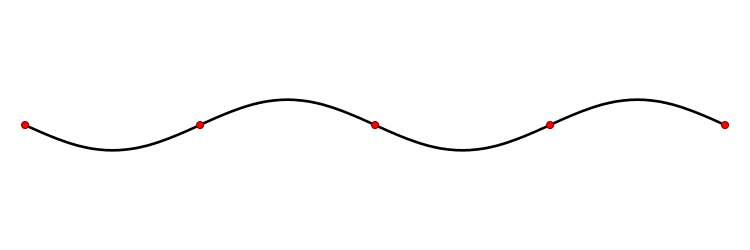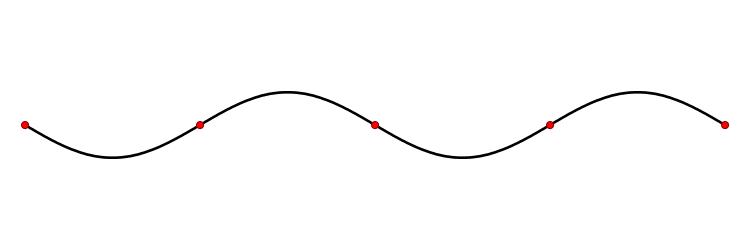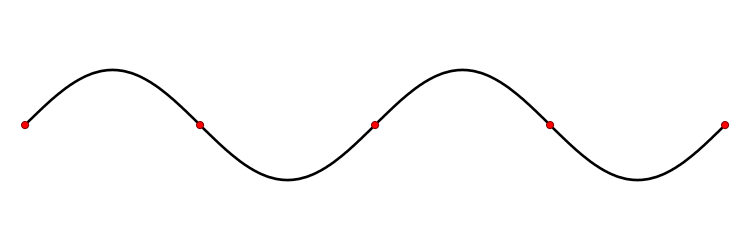
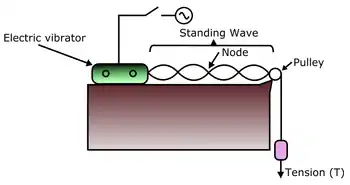
Les ondes mécaniques transversales produites sur la corde par un vibreur électrique se propagent jusqu'à une poulie. Là, une masse tend la corde, de sorte que l'onde incidente se réfléchit et repart dans le sens opposé. La rencontre et la superposition des ondes incidentes et réfléchies est à l'origine d'un phénomène d'interférence d'ondes. En fixant la distance entre le vibreur et la poulie, on peut déterminer une tension appropriée pour laquelle apparaissent des ondes stationnaires. On distingue alors des points sur cette onde qui demeurent immobiles, appelés nœuds.
L'expérience met en avant les modes propres de la corde[5]. On peut alors observer un nombre infini dénombrable de modes de vibration possibles, tous étant un multiple entier d'une fréquence fondamentale.
Démonstration du résultat
Il est possible de démontrer l'apparition d'une onde stationnaire sur la corde à l'aide du principe fondamental de la dynamique.
Mise en équation du problème
On considère une corde homogène de longueur L, supposée inélastique, masse linéique μ, initialement au repos et confondue avec l'axe Ox des abscisses. La corde est tendue par une tension uniforme et constante, notée T. La corde est tendue et fixée aux deux extrémités en x = 0 et en x = L.
On étudie les petits mouvements transversaux de la corde dans le plan xOy autour de sa position d'équilibre. L'élongation de la corde en un point M à l'instant t est notée y(x,t). On négligera l'action de la pesanteur devant les autres forces ainsi que toute cause d'amortissement.
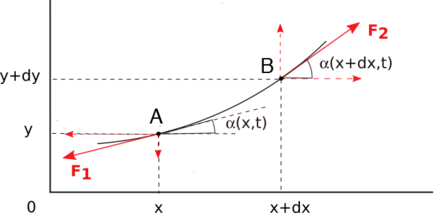
- Système : {tronçon de corde situé entre x et x+dx}
- Référentiel : laboratoire (supposé galiléen)
- Bilan des actions extérieures :
- Poids du tronçon : (négligé devant les autres forces) ;
- Force (tension) exercée par la partie à gauche de : ;
- Force (tension) exercée par la partie à droite de : .
- PFD :
- où est l'accélération.
- Projection sur l'axe Ox :
- (car il n'y a pas de déplacement horizontal donc pas accélération).
- Projection sur l'axe Oy :
- (avec la composante verticale de l'accélération).
- Comme on s'intéresse à de petites variations d'angles, on peut linéariser à l'ordre 1. Les deux équations précédentes deviennent alors :Or comme les angles sont faibles, alors on a alors à l'ordre 1: . D'où :
- Par ailleurs : . L'équation [Eq. 1] devient donc :
- On reconnait une équation de d'Alembert de la forme , où est homogène à une vitesse et correspond à la célérité de l'onde mécanique sur la corde[6].
Résolution de l'équation
Les ondes générées par le vibreur électrique sont des ondes harmoniques (sinusoïdales) unidimensionnelles, donc les solutions de l'équation de d'Alembert sont les fonctions de la forme :
, où est une constante réelle, est la célérité de l'onde, et et sont les phases à l'origine.
En utilisation la formule trigonométrique de factorisation , on transforme l'expression en :
Conditions limites
- La corde étant fixée en , cette condition impose quel que soit , c'est-à-dire :
.
L'équation [Eq. 2] devient donc:
- La corde étant aussi fixe en , on a , soit :
.
Famille de solutions

Finalement, avec les conditions aux limites, on obtient une famille de solutions telles que :
Par analogie avec les oscillations libres d'un oscillateur harmonique unidimensionnel en mécanique du point, ces solutions sont appelées modes propres de la corde et leurs pulsations sont appelées pulsations propres de la corde.
Interprétation des solutions
On a montré que les conditions aux limites imposaient . Les pulsations sont donc quantifiées. Cette relation s'interprète en faisant apparaître la longueur d'onde et la fréquence :
soit [8].
Cette égalité traduit le fait que pour une longueur d'onde donnée, la longueur L de la corde doit être un multiple entier d'une demi longueur d'onde pour qu'apparaissent des ondes stationnaires.
La fréquence étant liée à la pulsation par la relation , on observe que la fréquence des oscillations ne peut prendre qu'un certain nombre de valeurs pour qu'apparaissent des ondes stationnaires sur la corde. Toutes ces fréquences sont multiples de la fréquence fondamentale (fréquence minimale pour qu'une onde stationnaire apparaisse sur la corde).
Notes et références
- Melde, Franz. Ueber einige krumme Flächen, welche von Ebenen, parallel einer bestimmten Ebene, durchschnitten, als Durchschnittsfigur einen Kegelschnitt liefern: Inaugural-Dissertation... Koch, 1859.
- Melde, Franz. "Ueber die Erregung stehender Wellen eines fadenförmigen Körpers." Annalen der Physik 185, no. 2 (1860): 193-215.
- Melde, Franz. Die Lehre von den Schwingungscurven...: mit einem Atlas von 11 Tafeln in Steindruck. JA Barth, 1864.
- Melde, Franz. "Akustische Experimentaluntersuchungen." Annalen der Physik 257, no. 3 (1884): 452-470.
- Geneviève Tulloue, « Corde de Melde (Animation Flash) », sur sciences.univ-nantes.fr (consulté le )
- Bertrand Hauchecorne, Formulaire Maths - Physique - Chimie : SII - 2e édition, Paris, Ellipses, , 393 p. (ISBN 978-2-340-00663-8), p. 289
- Christophe More et Stéphane Olivier, Physique 2e année PSI PSI*, Paris, Tec & Doc Lavoisier, coll. « Référence Prépas », , 846 p. (ISBN 978-2-7430-1128-4), p. 720
- Louis-Thomas Nessi, Alexis Dubois, Eric Gillette, Dan Levy et Gilles Mentré, Methodix Physique 1, Ellipses, coll. « Methodix », , 380 p. (ISBN 978-2-7298-5702-8), p. 204












![{\displaystyle -T\,{\frac {\partial y}{\partial x}}(x,\,t)+T{\frac {\partial y}{\partial x}}(x+\mathrm {d} x,\,t)=\mu \,\mathrm {d} x\,{\frac {\partial ^{2}y}{\partial t^{2}}}(x,\,t)\qquad \qquad [{\rm {Eq.\,1].}}}](https://img.franco.wiki/i/9d0aaf6846b48088d078d382b2476d49d92aa5a1.svg)




![{\displaystyle y(x,t)=A\,\cos \left(\omega \left[t-{\frac {x}{c}}\right]+\varphi \right)+A\,\cos \left(\omega \left[t+{\frac {x}{c}}\right]+\psi \right)}](https://img.franco.wiki/i/13e19e58aadb4aee910f0c36d236fbf02114ef1b.svg)




![{\displaystyle y(x,t)=2\,A\,\cos \left(\omega \,t+{\frac {\varphi +\psi }{2}}\right)\cos \left({\frac {\omega \,x}{c}}-{\frac {\varphi -\psi }{2}}\right)\quad \Longleftrightarrow \quad y(x,t)=B\,\cos \left(\omega \,t+\alpha \right)\cos \left({\frac {\omega \,x}{c}}-\beta \right)\qquad \qquad {\rm {[Eq.\,2].}}}](https://img.franco.wiki/i/63233ee0cc770e20a8e028486e35b4dc3ffc04ab.svg)















