Estimateur de Kaplan-Meier
L'estimateur de Kaplan-Meier[1] - [2], également connu sous le nom de l’estimateur produit-limite, est un estimateur pour estimer la fonction de survie d’après des données de durée de vie. En recherche médicale, il est souvent utilisé pour mesurer la fraction de patients en vie pour une certaine durée après leur traitement. Il est également utilisé en économie et en écologie.
Cet estimateur doit son nom à Edward L. Kaplan et Paul Meier.
Une courbe d’estimation de Kaplan-Meier pour la fonction de survie est une série de marches horizontales de grandeur décroissante qui, quand un échantillon suffisamment grand est utilisé, permet d’approcher la fonction de survie réelle dans cette population. La valeur de la fonction de survie entre les échantillons successifs observés est considérée comme étant constante.
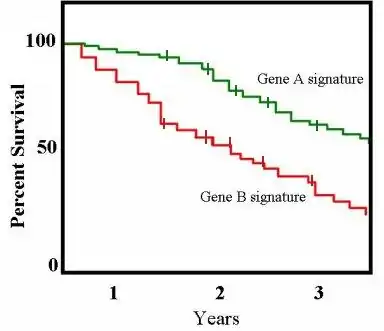
Un avantage important de la courbe de Kaplan-Meier est que cette méthode peut prendre en compte certains types de données censurées, en particulier censurées par la droite, ce qui intervient lorsqu’un patient disparaît d’une étude, c’est-à-dire qu’on ne dispose plus de ses données avant que l’événement attendu (par exemple le décès), soit observé. Sur le graphique, les petits traits verticaux indiquent ces censures. Si aucune troncature ou censure n’intervient, la courbe de Kaplan-Meier est équivalente à la fonction de survie.
Formules
Soit S(t) la probabilité qu’un membre d’une population donnée ait une durée de vie supérieure à t. Pour un échantillon de taille N dans cette population, les durées observées jusqu’à chaque décès des membres de l’échantillon N sont :
À chaque ni correspond un ti, ni étant le nombre de personnes « à risque » juste avant le temps ti, et di le nombre de décès au temps ti.
On note que les intervalles entre chaque évènement ne sont pas uniformes. Par exemple, une petite quantité de données peut commencer avec 10 cas. Supposons que le sujet 1 décède au jour 3, les sujets 2 et 3 au jour 11 et le sujet 4 disparaît du suivi (donnée censurée) au jour 9. Les données pour les 2 premiers sujets seraient les suivantes :
| 1 | 2 | |
|---|---|---|
| 3 | 11 | |
| 1 | 2 | |
| 10 | 8 |
L’estimateur de Kaplan-Meier est l’estimation du maximum de vraisemblance non-paramétrique de S(t). C’est un produit de la forme :
Lorsqu’il n’y aucune censure, ni est le nombre de survivants juste avant le temps ti.
Lorsqu’il y a censure, ni est le nombre de survivants moins le nombre de pertes (cas censurés). Ce sont seulement ces cas survivants qui continuent à être observés (qui n’ont pas encore été censurés) qui sont « à risque » de décès (observé).
Ici une autre définition possible parfois utilisée :
Les deux définitions diffèrent uniquement aux moments des évènements observés. La dernière définition est « continue à droite » tandis que la première est « continue à gauche ». Soit T la variable aléatoire qui mesure le temps d’échec et soit F(t) sa Fonction de répartition cumulative. On note que :
En conséquence, la définition continue à droite de peut être préférée pour rendre l’estimation compatible avec une estimation continue à droite de F(t).
Considérations statistiques
L’estimateur de Kaplan-Meier est une statistique, et certains estimateurs sont utilisés pour approcher sa variance. Un de ces estimateurs les plus courants est la formule de Greenwood :
Genèse de l'estimateur de Kaplan-Meier
En 1983, Edward L. Kaplan raconte la genèse de l'estimateur de Kaplan-Meier[3].
Le tout débute en 1952, révèle Kaplan, quand Paul Meier (alors en stage post-doctoral à l'université Johns-Hopkins, au Maryland), après avoir pris connaissance de l'article de Greenwood, publié en 1926, sur la durée du cancer, veut proposer un puissant estimateur de survie appuyé sur les résultats d'essais cliniques. En 1953, le mathématicien Kaplan (travaillant alors aux Laboratoires Bell, au New Jersey) veut proposer un estimateur de la durée qu'auront les tubes à vide utilisés pour amplifier et retransmettre les signaux dans le système de câbles téléphoniques sous-marins. Kaplan soumet son projet d'article au professeur John W. Tukey, qui œuvrait aussi pour les Laboratoires Bell et qui venait d'être maître de thèse de Meier[4] à Princeton, au New Jersey. Chacun des deux jeunes chercheurs avait soumis son manuscrit au Journal of the American Statistical Association, qui leur recommandait d'entrer en contact l'un avec l'autre, pour fusionner les deux articles. Alors, Kaplan et Meier entreprennent, par correspondance (courrier postal), de réconcilier leurs points de vue. Durant les quatre ans que dure cette phase, leur seule crainte est qu'un tiers publie avant eux un article proposant une solution équivalente.
L'article Nonparametric estimation from incomplete observations est finalement publié en 1958 (Journal of the American Statistical Association, vol. 53, p. 457–481)[1].
Implémentation dans les langages de programmation
Plusieurs langages de programmation et logiciels statistiques proposent des implémentations de l'estimateur de Kaplan-Meier. On peut notamment citer :
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Kaplan–Meier estimator » (voir la liste des auteurs).
- Kaplan, E. L.; Meier, P.: Nonparametric estimation from incomplete observations. J. Amer. Statist. Assn. 53:457–481, 1958.
- Kaplan, E.L. in a retrospective on the seminal paper in "This week's citation classic". Current Contents 24, 14 (1983). Available from UPenn as PDF.
- Le 15 avril 1983, Edward L. Kaplan (alors du Department of Mathematics, de l'université d'État de l'Oregon) raconte la genèse de l'article de 1958 présentant l'estimateur de Kaplan-Meier — notule de rétrospective parue dans la section « This week's citation classic » du Current Contents, no 24, du 13 juin 1983 — notule retransmise par l'université de Pennsylvanie [(en) lire en ligne (page consultée le 15 août 2011)].
- « Appendix C: Ph.D. Students », p. 1569 de : (en) David R. Brillinger, « John W. Tukey: His life and professional contributions », Annals of Statistics, Department of Statistics University of California, vol. 30, no 6, , p. 1535-1575 (lire en ligne)
- The LIFETEST Procedure
- (en) « survival: Survival Analysis », R Project
- (en) Frans Willekens, Multistate Analysis of Life Histories with R, Cham, Springer, , 323 p. (ISBN 978-3-319-08383-4, DOI 10.1007/978-3-319-08383-4_6, lire en ligne), « The Survival Package »
- (en) Ding-Geng Chen et Karl E. Peace, Clinical Trial Data Analysis Using R, CRC Press, , 99–108 p. (lire en ligne)
- (en) « sts — Generate, graph, list, and test the survivor and cumulative hazard functions », Stata Manual
- (en) Mario Cleves, An Introduction to Survival Analysis Using Stata, College Station, Stata Press, , Second éd., 372 p. (ISBN 978-1-59718-041-2 et 1-59718-041-6, lire en ligne)
- (en) « lifelines ».
- « sksurv.nonparametric.kaplan_meier_estimator — scikit-survival 0.12.1.dev4+gba84551.d20200501 documentation », sur scikit-survival.readthedocs.io (consulté le )







![S(t)=P[T>t]=1-P[T\leq t]=1-F(t).\,](https://img.franco.wiki/i/025e8227464c480f59905f7ee7186911513a06a0.svg)

