Espace de Cartan-Alexandrov-Toponogov

Illustration du théorème de comparaison de Toponogov : le triangle de gauche, en courbure négative, est plus "fin" que son homologue euclidien

La géométrie riemannienne fournit à la fois les espaces modèles auxquels les espaces CAT(k) sont comparés, et le principe de cette comparaison. Les espaces modèles sont les espaces de courbure sectionnelle constante égale à k, et qui sont simplement connexes. On montre que pour k>0 il s'agit d'une sphère de rayon ${\displaystyle {\frac {1}{\sqrt {k}}}}$, pour k<0 c'est un espace hyperbolique et pour k=0 c'est l'espace euclidien.

Sur une variété riemannienne générale on peut étudier la forme des triangles géodésiques et la comparer à la forme des triangles des espaces de référence. Le théorème de comparaison de Toponogov fournit un résultat global de comparaison : lorsqu'on dispose d'un encadrement de la courbure sectionnelle entre deux constantes m et M, on peut encadrer (du moins si le triangle n'est pas « trop gros ») la longueur du troisième côté entre la valeur qu'elle aurait sur une variété de courbure constante m et celle sur une variété de courbure constante M. La question de la paternité de ce résultat est assez complexe, mais il apparaît dans sa version finale en 1959[1].

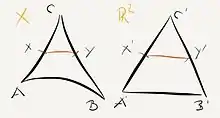
On considère un nombre réel k et l'espace modèle ${\displaystyle M_{k}}$ correspondant. Soit un espace métrique géodésique (E,d). Cet espace est qualifié d'espace CAT(k) si, pour chaque triangle géodésique T rejoignant trois points x,y,z de E, il existe un triangle de comparaison T' dans l'espace modèle ${\displaystyle M_{k}}$ vérifiant

• les côtés de T et de T' sont tous les trois de même longueur ;
• les distances entre tous les points de T sont inférieures aux distances entre les points homologues de T'.

Plus précisément, pour k>0, on ne considère dans cette définition que les triangles T de périmètre inférieur à deux fois le diamètre de l'espace modèle ${\displaystyle M_{k}}$.

Bien évidemment, puisque la comparaison se fait dans un seul sens, un espace CAT(k) est également CAT(k') pour tout k'>k.