Epsilon transition

Des cas particuliers importants sont notamment :

• automate fini
• automate à pile
• machine de Turing

Un automate reconnaissant ${\displaystyle a^{*}b^{*}}$ avec une ε-transition de 1 à 2.

L'automate après élimination de la transition spontanée par fermeture arrière.

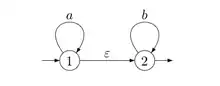
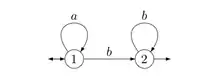
L'automate ci-contre est asynchrone : il possède une ε-transition de l'état 1 vers l'état 2. L'élimination des ${\displaystyle \varepsilon }$-transitions se fait par un algorithme de fermeture transitive. Appelons ε-chemin un chemin formé uniquement de ε-transitions. On peut alors procéder de deux façons différentes mais équivalentes, appelées fermeture avant et fermeture arrière par Sakarovitch[2], comme suit :

• (fermeture avant) Pour chaque transition d'un état ${\displaystyle s}$ à un état ${\displaystyle t}$ portant une lettre ${\displaystyle a}$ et pour chaque ε-chemin de ${\displaystyle t}$ à un état ${\displaystyle u}$, ajouter une transition de ${\displaystyle s}$ à ${\displaystyle u}$ d'étiquette ${\displaystyle a}$ ;
• (fermeture arrière) Pour chaque ε-chemin d'un état ${\displaystyle s}$ à un état ${\displaystyle t}$ et pour chaque transition de ${\displaystyle t}$ à un état ${\displaystyle u}$ portant une lettre ${\displaystyle a}$, ajouter une transition de ${\displaystyle s}$ à ${\displaystyle u}$ d'étiquette ${\displaystyle a}$ ;

Pour les états initiaux et terminaux, on complète par :

• (fermeture avant) Pour chaque ε-chemin d'un état ${\displaystyle s}$ initial à un état ${\displaystyle t}$, ajouter ${\displaystyle t}$ à l'ensemble des états initiaux.
• (fermeture arrière) Pour chaque ε-chemin d'un état ${\displaystyle s}$ à un état terminal ${\displaystyle t}$, ajouter ${\displaystyle s}$ à l'ensemble des états terminaux.

Bien entendu, on supprime les ${\displaystyle \varepsilon }$-transitions. Dans l'exemple de la figure, on ajoute la transition ${\displaystyle 1{\xrightarrow {b}}2}$ dans la première étape en fermeture arrière, et on déclare que ${\displaystyle 1}$ est état final dans la deuxième étape. Si on opère par fermeture avant, on ajoute la transition ${\displaystyle 1{\xrightarrow {a}}2}$ et on déclare ${\displaystyle 2}$ comme état initial.

La complexité en temps est celle du calcul d'une fermeture transitive, puisque l’on détermine les ε-chemins.

Une transition spontanée se produit dans un automate à pile en présence d'une ε-règle, c'est-à-dire d'une règle qui ne consomme pas de lettre d'entrée. Ces automates sont appelées automate en temps réel. On peut montrer[3] que tout langage algébrique peut être reconnu par un automate à pile en temps réel et ne possédant qu'un seul état.

En revanche, tout langage algébrique déterministe ne peut pas être reconnu par un automate à pile déterministe en temps réel.

La notion de ε-transition n’apparaît pas explicitement : elle est comprise dans le comportement qui consiste à ne pas modifier le symbole lu sur la bande. La règle de transition stipule donc que la lettre « écrite » est la même que la lettre « lue ».

• (en) John E. Hopcroft, Rajeev Motwani et Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley, 2007, 3^e éd. (ISBN 978-0-32146225-1)
• Jacques Sakarovitch, Éléments de théorie des automates, Vuibert, 2003, 816 p. (ISBN 978-2-7117-4807-5) — Traduction anglaise avec corrections : (en) Elements of Automata Theory, Cambridge, Cambridge University Press, 2009, 758 p. (ISBN 978-0-521-84425-3)
• Jean-Michel Autebert, Jean Berstel et Luc Boasson, « Context-free languages and pushdown automata », dans G. Rozenberg et A. Salomaa (éditeurs), Handbook of Formal Languages, vol. 1 : Word, Language, Grammar, Springer Verlag, 1997 (ISBN 978-3540604204), p. 111--174