Automate à pile

Un automate à pile est une machine abstraite utilisée en informatique théorique et, plus précisément, en théorie des automates.

Un automate à pile est une généralisation des automates finis : il dispose en plus d'une mémoire infinie organisée en pile (last-in/first-out ou LIFO). Un automate à pile prend en entrée un mot et réalise une série de transitions. Il effectue pour chaque lettre du mot une transition, dont le choix dépend de la lettre, de l'état de l'automate et du sommet de la pile ; il peut aussi modifier le contenu de la pile. Selon l'état de l'automate et de la pile à la fin du calcul, le mot est accepté ou refusé.

Les langages reconnus par les automates à piles sont exactement les langages algébriques, c'est-à-dire ceux engendrés par une grammaire algébrique.

L'importance des automates à pile vient de leur emploi en analyse syntaxique des langages de programmation, et plus généralement dans la transformation de définitions ou d'algorithmes récursifs en leurs analogues itératifs.

Un automate à pile. Une unité de contrôle finie agit en lisant la donnée sur la bande d'entrée (input tape), et en utilisant une mémoire auxiliaire en forme de pile (stack).

Définition formelle

Automate à pile

Un automate à pile (non déterministe) est un 7-uplet ${\mathcal {A}}=(Q,A,Z,\delta ,z_{0},q_{0},T)$ , où :

$Q$ est l'ensemble d'états ;
$A$ est l'alphabet d'entrée ;
$Z$ est l'alphabet de pile ;
$\delta :Q\times (A\cup \{\varepsilon \})\times Z\rightarrow {\mathcal {P}}(Q\times Z^{*})$ est la fonction de transition (la notation ${\mathcal {P}}$ désigne l'ensemble des parties) ;
$z_{0}\in \ Z$ est le symbole de fond de pile ;
$q_{0}\in Q$ est l'état initial ;
$T\subset Q$ est l'ensemble des états terminaux.

Au lieu de la fonction $\delta$ , on rencontre fréquemment l'ensemble $\Delta \subset Q\times (A\cup \{\varepsilon \})\times Z\times Q\times Z^{*}$ défini par

(q,y,z,p,h)\in \Delta \iff (p,h)\in \delta (q,y,z)

Les éléments de $\Delta$ sont les règles de transitions. Lorsque $y=\varepsilon$ , on parle d'une $\varepsilon$ -règle. Tous les ensembles dans la définition sont finis.

Une configuration interne de l'automate est un couple $(q,h)\in Q\times Z^{*}$ . Une configuration de l'automate est un triplet $(q,w,h)\in Q\times A^{*}\times Z^{*}$ . Un calcul de l'automate sur un mot $w\in A^{*}$ est une suite de transitions à partir de la configuration initiale $(q_{0},w,z_{0})$ . Il y a transition de la configuration $(q,yw,zh)$ , où $y\in A\cup {\varepsilon }$ et $z\in Z$ vers la configuration $(q',w,h'h)$ et on écrit :

(q,yw,zh)\vdash (q',w,h'h)

lorsque $(q',h')\in \delta (q,y,z)$ . Lorsque $y=\varepsilon$ , le mot d'entrée ne change pas. On parle alors d'une $\varepsilon$ -transition ou d'une transition spontanée. Dans tous les cas, pour qu'une transition soit possible, la pile ne doit pas être vide.

On dit qu'un mot est accepté par l'automate s'il existe une série de transitions qui conduit à une configuration acceptante. Plusieurs modes de reconnaissance existent :

Reconnaissance par pile vide. Les configurations acceptantes sont les configurations de la forme $(q,\varepsilon ,\varepsilon )$ où $q\in Q$ est un état quelconque. Autrement dit, il est possible d'arriver à vider entièrement la pile au moment où on termine la lecture du mot.
Reconnaissance par état final. Les configurations acceptantes sont les configurations de la forme $(t,\varepsilon ,h)$ où $t\in T$ est un état final. La pile n'est donc pas nécessairement vide à la fin de la lecture du mot.
Reconnaissance par pile vide et état final. Les configurations acceptantes sont les configurations de la forme $(t,\varepsilon ,\varepsilon )$ où $t\in T$ est un état final. La pile est vide à la fin de la lecture du mot.

Le langage reconnu par l'automate ${\mathcal {A}}$ est l'ensemble des mots de $A^{*}$ qui sont acceptés.

Les trois modes d'acceptation sont équivalents, au sens que si un langage est reconnu par un automate à pile d'une espèce, on peut construire un automate reconnaissant ce langage, des autres espèces.

Commentaires

Un automate à pile est composé de deux parties qui interagissent : la partie automate, avec un nombre fini d'états, et une mémoire auxiliaire infinie, organisée en pile. On s'attendrait donc d'avoir deux opérations sur la pile, une pour empiler un symbole, une pour en dépiler un. La définition mathématique adoptée consiste à remplacer ces deux opérations par une seule qui les combine et qui, dans des cas particuliers, donne les opérations d'empilement et de dépilement. En effet, si on applique une règle de transition

(q,y,z,p,h)

on dépile d'abord le symbole $z$ , puis on empile le mot $h$ , donc $z$ est remplacé par $h$ . Si le mot $h$ est vide, l'opération consiste donc simplement à dépiler ; si le mot $h$ commence par $z$ , donc si $h=zh'$ , l'opération revient à empiler, par-dessus $z$ , une autre mot $h'$ . Un troisième avantage de cette notation compactée est que l'on peut tester quelle est la nature du symbole en haut de pile, simplement en le lisant et en le remettant.

Dans le formalisme présenté, on ne peut pas tester si la pile est vide, car si la pile est vide, tout calcul (qui doit commencer par un dépilement) est impossible. Une façon de contourner cette difficulté est d'utiliser un symbole spécial de fond de pile que l'on n'enlève pas.

Automate à pile déterministe

Un automate à pile est déterministe lorsque la fonction de transition est une fonction partielle vérifiant une condition supplémentaire.

Plus précisément, $\delta$ est une fonction partielle $Q\times (A\cup \{\epsilon \})\times Z\rightarrow Q\times Z^{*}$ . De plus, lorsque $\delta (q,\epsilon ,z)$ est définie, alors $\delta (q,a,z)$ n'est définie pour aucune lettre $a\in A$ . Ainsi, si une transition spontanée est possible, aucune autre transition ne l'est à partir de cette configuration.

Les modes de reconnaissance, par état final ou par pile vide, ne sont plus équivalents. Un langage algébrique déterministe est un langage algébrique pour lequel il existe un automate à pile déterministe par état final qui le reconnaît. Les automates déterministes avec reconnaissance par pile vide reconnaissent exactement les langages algébriques déterministes qui sont préfixes (aucun mot du langage n'est préfixe d'un autre mot du langage).

Par exemple, le langage $\{a^{n}b^{n}\mid n>0\}$ est préfixe, et est reconnu par les deux types d'automates déterministes, mais le langage $a^{*}$ ne l'est que par automate déterministe par état final.

Un exemple

Automate reconnaissant le langage $\{a^{k}b^{k}\mid k\geq 1\}$ .

L'automate a deux états $q,p$ ; l'état $q$ est initial, il n'y a pas d'état terminal. La reconnaissance est par pile vide. Le symbole de fond de pile est $\omega$ . Il y a un seul symbole de pile supplémentaire, noté $A$ . Les transitions sont :

(1)

(q,a,\omega ,q,A)

(2)

(q,a,A,q,AA)

(3)

(q,\varepsilon ,A,p,A)

(4)

(p,b,A,p,\varepsilon )

La troisième règle est une $\varepsilon$ -règle. Elle dit que, de l'état $q$ , on peut passer à l'état $p$ sans rien lire, et sans changer la pile.

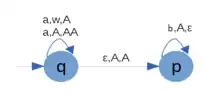
représentation d'un automate à pile

On commence par lire le premier caractère :

si le mot est vide, on a fini et le mot est rejeté car la pile n’est pas vide ;
si c'est un $a$ , on remplace le fond de pile par $A$ ;
si c'est un $b$ , le mot est rejeté parce qu'aucune règle ne s'applique.

Ensuite, à chaque $a$ lu, on empile un $A$ additionnel par la règle (2). Après avoir lu $k$ lettres $a$ consécutivement, la pile contient $A^{k}$ . Si on voit un $b$ , tout en étant dans l'état $q$ , la machine se bloque parce qu'aucune règle ne s'applique.

Dans l'état $q$ , la règle (3) fait passer dans l'état $p$ , sans lecture de lettre ni de modification de la pile. Ensuite, seule la règle (4) s'applique, et on peut l'appliquer tant que la pile n'est pas vide, c'est-à-dire autant de fois que l’on a lu des lettres $a$ . L'acceptation par pile vide signifie que le mot lu est accepté quand la pile est vide, donc quand le mot a la forme $a^{k}b^{k}$ .

L'exemple serait plus compliqué si on voulait éviter la $\varepsilon$ -règle.

Propriétés

Chaque langage défini par une grammaire algébrique est reconnu par un automate à pile et réciproquement.

En conséquence, le problème de l'appartenance d'un mot à un langage algébrique est décidable : il existe un algorithme qui, étant donnés la description d'une grammaire non contextuelle et un mot, répond en temps fini à la question de l'appartenance de ce mot au langage défini par cette grammaire (plus précisément, on peut le tester en un temps $O(n^{3})$ pour un mot de longueur n, grâce à l'algorithme CYK).

La classe des langages rationnels (reconnus par des automates finis) est strictement incluse dans la classe des langages algébriques déterministes (reconnus par automate à pile déterministe par état final), elle-même strictement incluse dans la classe des langages algébriques (reconnus par des automates à pile non déterministes). Par exemple, le langage $a^{n}b^{n}$ est algébrique déterministe mais non rationnel, et le langage des mots palindromes est algébrique mais pas algébrique déterministe.

Restrictions et extensions

Modes d'acceptation

D'autres variantes d'acceptation existent. C'est pourquoi on rencontre parfois une formulation qui sépare la définition en deux : d'une part, une machine à pile est définie sans préciser le mode d'acceptation. D'autre part, une automate est spécifié par la donnée des configurations internes d'acceptation. Par exemple :

l'ensemble $Q\times \{\varepsilon \}$ décrit l'acceptation par pile vide ;
l'ensemble $T\times Z^{*}$ décrit l'acceptation par état final ;
l'ensemble $T\times \{\varepsilon \}$ décrit l'acceptation par état final et pile vide.

Automate en temps réel

Un automate à pile est dit en temps réel (realtime en anglais) s'il ne possède pas de $\varepsilon$ -règles. Un automate à pile est simple s'il ne possède qu'un seul état. On peut montrer[1] que tout langage algébrique propre (c'est-à-dire ne contenant pas le mot vide) peut être reconnu par un automate à pile en temps réel et simple.

En revanche, tout langage déterministe ne peut pas être reconnu par un automate à pile déterministe en temps réel. Par exemple, le langage

\{a^{n}b^{p}ca^{n}\mid n,p>0\}\cup \{a^{n}b^{p}db^{p}\mid n,p>0\}

est algébrique et déterministe, mais ne peut être reconnu par un automate à pile déterministe en temps réel[1].

Langage de pile

Le langage de pile d'un automate à pile est l'ensemble des mots qui apparaissent sur la pile lors d'un calcul réussi, c'est-à-dire dans une configuration d'une suite de transitions à partir de la configuration initiale vers une configuration acceptante. Pour tout automate à pile, et quel que soit le mode d'acceptation, le langage de pile est un langage rationnel[1]. La nature du langage de pile – et plus généralement du langage des mémorisations intermédiaires – a été étudiée systématiquement par Oscar H. Ibarra et IanMcQuillan[2].

Automates à deux piles

Un automate à deux piles ou plus a la même puissance de calcul qu'une machine de Turing. En effet, les automates à deux piles sont une généralisation des machines à deux compteurs, elles-mêmes équivalentes aux machines de Turing. On peut aussi le démontrer de manière plus directe : un automate à deux piles peut simuler une machine de Turing, en faisant en sorte que la partie du ruban située à gauche de la tête de lecture soit enregistrée dans la première pile, et que la partie du ruban située à droite de la tête de lecture soit enregistrée sur la seconde.

L'équivalence des automates à pile déterministes

Géraud Sénizergues a prouvé, en 2001, que l'équivalence de deux automates à pile déterministes est décidable. Ce problème était ouvert depuis la définition des automates déterministes dans les années 1970. Géraud Sénizergues a obtenu le prix Gödel pour cette preuve.

Applications

La plupart des langages de programmation sont décrits par une grammaire algébrique. L'analyse syntaxique d'un programme, qui est une des premières opérations effectuées par un compilateur, peut donc être effectuée par un automate à pile. Si la grammaire du langage est une grammaire algébrique déterministe, il suffit de construire un automate à pile déterministe ; sinon, on doit construire un automate à pile non déterministe.

Il existe des outils pour construire automatiquement un automate à pile à partir d'une description de la grammaire d’un langage (par exemple, ANTLR).

Implémentation d'un automate à pile

Le programme suivant (en langage C) vérifie que l'expression entrée respecte le langage des parenthèses où toute parenthèse ouvrante doit correspondre à une parenthèse fermante :

#include <stdlib.h>
#include <stdio.h>
#define POP       -1  /* Dépiler l'état               */
#define ACCEPT    -2  /* Accepter l'expression entrée */
#define ERROR     -3  /* Refuser l'expression entrée  */
#define ALPHABET 3    /* Grandeur*/
/*
    Push-down automation
    Symbol   | (       | )        | \0
    ---------+---------+--------+-----------
    State 0  | PUSH 1  | ERROR  | ACCEPT
    State 1  | PUSH 1  | POP    | ERROR
*/
int states[2][ALPHABET*2] =
{
    /* Valeur d'entrée    Action     */
    {
            '(',          1 /* PUSH 1 */,
            ')',          ERROR,
            '\0',         ACCEPT
    },
    {
            '(',          1 /* PUSH 1 */,
            ')',          POP,
            '\0',         ERROR
    }
};
int main( int argc, char** argv )
{
    int    stack[100]  = { 0 };
    int    i           = 0;
    int    action      = 0;
    int*   tos         = stack;
    char   s[80+1];
    char*  p           = s;
    /* Chaine de donnée */
    printf("Entrez l'expression : ");
    fgets( &s , 80 , stdin);     // modification pour éviter les débordements de mémoire
    /* État initial 0 mis dans la pile : */
    *(tos++) = 0;
    /* Sortie */
    do
    {
        /* Recherche de l'action correspondant au symbole d'entrée courant... */
        action = ERROR; /* Action par défaut si le symbole n'est pas trouvé. */
        for( i = 0; i < ALPHABET; i++ )
        {
            if( states[*(tos-1)][i*2] == *p )
            {
                /* Caractère entré trouvé */
                action = states[*(tos-1)][i*2+1];
                break;
            }
        }
        /* Effectuer l'action associée au symbole d'entrée courant... */
        if( action == ERROR )
        {
            printf("Erreur inattendue à la position %d", p-s);
            break;
        }
        else if( action == ACCEPT )
            printf("Sortie acceptée !");
        else if( action == POP )
            tos--;             /* Dépiler l'état */
        else
            *(tos++) = action; /* Empiler l'état spécifié */
        /* Données supplémentaires... */
        p++;
    }
    while( action != ACCEPT );
    getchar();
    return 0;
}

Notes et références

Notes

Autebert, Berstel, Boasson (1997), p. 34 : « The fact that any proper context-free language can be generated by a context-free grammar in Greibach normal form implies that realtime pda's, (and even simple pda's), recognize exactly proper context-free languages. ».
Oscar H. Ibarra et Ian McQuillan, « On store languages of language acceptors », Theoretical Computer Science, vol. 745,‎ 2018, p. 114-132 (DOI 10.1016/j.tcs.2018.05.036).

Références

Références générales

Olivier Carton, Langages formels, calculabilité et complexité, 2008 [détail de l’édition] (lire en ligne)
Jean-Michel Autebert, Jean Berstel et Luc Boasson, « Context-free languages and pushdown automata », dans G. Rozenberg, A. Salomaa (éditeurs), Handbook of Formal Languages, vol. 1 : Word, Language, Grammar, Springer Verlag, 1997 (ISBN 978-3540604204), p. 111--174

Sur l'équivalence des automates à pile déterministe

Géraud Sénizergues, « L(A)=L(B)? decidability results from complete formal systems », Theoretical Computer Science, vol. 251, n^os 1-2,‎ 2001, p. 1-166
Géraud Sénizergues, « L(A)=L(B)? A simplified decidability proof », Theoretical Computer Science, vol. 281, n^os 1-2,‎ 2002, p. 555-608
Géraud Sénizergues, « The Bisimulation Problem for Equational Graphs of Finite Out-Degree », SIAM Journal on Computing, vol. 34, n^o 5,‎ 2005, p. 1025–1106 (DOI 10.1137/S0097539700377256).
Petr Jančar, « Equivalence of pushdown automata via first-order grammars », Journal of Computer and System Sciences, vol. 115,‎ 2021, p. 86–112 (DOI 10.1016/j.jcss.2020.07.004).

Annexes

Articles connexes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.