Effet Coandă

Un effet Coandă très simple peut être observé en approchant tangentiellement du corps arrondi d'une bouteille le flux d'air d'un sèche-cheveux, qui se trouve dévié et contourne la bouteille. Un autre exemple bien connu de l'effet Coandă peut être observé à partir de l'expérience souvent nommée « de Bernoulli » qui place en lévitation aérodynamique une balle[2] au-dessus de la buse d'un sèche-cheveux. Si cette expérience peut être comprise assez facilement dans le cas où le sèche-cheveux délivre son souffle verticalement, la réflexion devient plus complexe lorsque l'on incline ce sèche-cheveux, situation où l'on constate que la balle reste captive du courant d'air. On peut penser que la balle est maintenue au-dessous du courant d'air par l'effet Coandă.

De même, dans le cas des balles de sport liftées on peut faire appel à l'effet Coandă. Lorsqu'une balle est projetée en avant et qu'elle est dotée d'un mouvement de rotation, la partie de l'air qui passe au-dessus de la balle est déviée vers le bas en contournant la balle (effet Magnus). La même expérience peut être réalisée sans effet Magnus en sustentant un tube à essais qui ne peut tourner et dont le fond arrondi est contourné par un jet dirigé vers le haut que le fond du tube à essais dévie vers le bas.

La constatation que le fluide suit la surface d’un corps convexe voisin et subit une déviation avant de s'en détacher avec une trajectoire différente de celle qu'il avait en amont est ancienne. Puis, le phénomène a été signalé à l’attention de la communauté scientifique en 1800 par le physicien britannique Thomas Young[3] - [4] dans les termes suivants :

« La pression latérale qui attire la flamme d’une bougie vers le flux d’air d’un tube de soufflage (de verrier) est peut-être exactement la même que la pression qui aide la déviation d’un courant d’air près d’un obstacle. Marquons l’impact produit par un mince filet d’air à la surface de l’eau. Mettons un corps convexe en contact avec le bord du filet, et la place de l’impact montrera aussitôt que le courant est dévié vers le corps ; et si le corps est libre de se mouvoir dans toutes les directions, il sera attiré vers le courant. »

La forme de la cuillère dévie le filet d'eau vers la gauche, selon l'effet théière, souvent improprement qualifié d'effet Coandă.

En quelques lignes Young a décrit des expériences qui permettent de produire le phénomène de déviation, de le reproduire et de le mesurer et en a énoncé une condition nécessaire : l’existence d’une pression latérale qui attire.

Henri Bouasse[5], professeur de physique à l’université de Toulouse, a repris en 1930 les expériences dont le principe avait été esquissé par Young. Bouasse précise que si un obstacle arrondi dévie vers lui le courant gazeux, le courant gazeux attire le corps arrondi, avec une force égale à la variation de la quantité de mouvement produite par la déviation du jet, en vertu du théorème d'Euler qui est l’application à un fluide en mouvement de la mécanique de Newton. Il explique aussi que le théorème de Bernoulli ne s'applique à aucun des phénomènes faisant l'objet de ses expériences : le jet crée en son voisinage un vide relatif dans un espace confiné où la vitesse est quasi nulle et la pression plus petite que dans le jet, donc l'équation de Bernoulli ne s'y applique pas.

Ce phénomène a été appliqué pour la première fois par l'aérodynamicien Henri Coandă : dans ses applications un gaz est émis par une fente mince dont une paroi est prolongée par une série de facettes planes de longueur croissante qui divergent progressivement de l’axe de la fente : le jet se réattache à la paroi après chaque discontinuité, il est ainsi progressivement dévié, en association avec une diminution de la pression à la paroi.
Selon Albert Métral (pt)[6], « L’effet Coandă, c’est les facettes » : mais on l’observe aussi dans de nombreux dispositifs dépourvus de facettes.

Dans les années 1950, ce thème connait un regain d'intérêt, en raison notamment de son intérêt dans la compréhension ou l'utilisation des phénomènes de déflexion dans l'aviation[7] - [8] - [9].

En 1965, un colloque est consacré à l'effet Coandă, les couches limites et les flux (jets) sur les parois à forte courbure[10] ; il inaugurait une nouvelle série de conférences européennes de recherche en mécanique et s'est tenu à Berlin les 5 et 6 avril 1965. Selon Wille & Fernholz qui ont produit un petit rapport à propos de cette conférence, l'année même, cette manifestation avait été limitée à une quarantaine de personnes, invitées en raison de leur intérêt actif pour ce sujet. Elle a été conçue comme un atelier de discussion et de travail, sans valeur officielle ni publication d'actes. Selon le rapporteur de la discussion orale K. Gersten, une seule communication faisait état de flux sur des parois à courbure vraiment forte, produisant ou non l'effet Coandă, mais en donnait une explication par un calcul de couche limite inacceptable[11]. Le premier auteur du rapport écrit était aussi le président du colloque[10]. L'année suivante I Reba publie un article sur les applications qui pourraient être faites de cet effet[12].

L’effet Coandă est un phénomène de mécanique des fluides.

Calcul de la pression sur une paroi circulaire de jet pariétal.

Les principaux phénomènes susceptibles de dévier un jet sont décrits ci-après ainsi que les conditions de cette déviation. La plupart des applications envisagées, notamment dans le domaine de l’aéronautique, impliquent un nombre de Reynolds plutôt élevé : 10⁶, rapport entre les forces d’inertie prépondérantes dans le jet et les forces de viscosité développées le long des surfaces environnantes dans la zone dépressionnaire engendrée : l’écoulement est turbulent, et peu modifié quand ce nombre de Reynolds varie. Le comportement à très bas nombre de Reynolds : 100 à 1 000, en régime laminaire a aussi été étudié.

Un effet Coandă, déviation d’un jet par une paroi convexe voisine, est susceptible de se produire de deux manières :

• jet libre : on approche une paroi convexe du bord de ce jet, qui suit la paroi entre un point d’attachement et un point de séparation. Philippe Poisson-Quinton, aérodynamicien de l’ONERA, a proposé le verbe « coander » pour désigner cette action qui dévie le jet vers une autre direction ;
• jet pariétal : l’orifice du jet est muni d’une paroi le prolongeant que le jet suit jusqu’à un point de séparation après lequel il part dans une direction différente.

Un jet pariétal bidimensionnel de largeur h suit une paroi circulaire de rayon r : il permet de déterminer dans quelles conditions l’effet Coandă se produit ou ne se produit pas en réalité.

Un jet d'air horizontal suivant une paroi plane de rayon r infini, ou mieux dont le rayon est le rayon de la Terre, suit la paroi sans se décoller, la pression de surface dans la couche limite comme la pression extérieure dans la zone de mélange avec l'air ambiant étant partout en équilibre avec la pression atmosphérique. Si le rayon est beaucoup plus petit, une « pression latérale » (T. Young), c.-à-d. une différence entre la pression atmosphérique extérieure et la pression de surface équilibre l’accélération centrifuge créée dans le jet dévié en suivant la paroi, le champ de pression produit étant déterminé par la courbure relative h/r, jusqu’à un point où il s’en sépare à la pression atmosphérique. Ce champ de pression est compris entre une zone à la sortie de l’orifice où il s’installe autour de la paroi circulaire, et une zone vers le point de séparation où il se défait.

Mesure des pressions sur une paroi circulaire de jet pariétal.

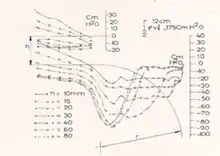
Des expériences datant de 1956 menées à un nombre de Reynolds de 10⁶[13] montrent l’influence du rapport h/r sur le champ de pression obtenu. L’image montre que quand le rapport h/r est supérieur à un rapport critique : 0,5 pour ce nombre de Reynolds, le champ de pression s’installe sur une longueur correspondant à un angle de 9 degrés, et est suivi d’une zone de longueur égale, où la pression remonte jusqu’à la pression atmosphérique au point de séparation de la couche limite soumise à ce gradient de pression. On n’observe que ces deux effets locaux qui ne sont pas un effet Coandă à proprement parler. Quand le rapport h/r est inférieur à 0,5, une déviation supplémentaire qu’on peut valablement qualifier d’effet Coandă véritable se produit dans une zone intermédiaire sur une longueur à une pression sensiblement constante, comme dans un jet pariétal le long d’une plaque plane, excepté que la couche limite soumise à une pression inférieure à la pression ambiante se décolle de la paroi.

Un calcul effectué dès 1954 en supposant le fluide parfait[14] prouve qu’en l’absence de viscosité il peut se produire une déviation d’un angle quelconque fixé d’avance, aussi grand qu’on veut, et quelle que soit la courbure relative h/r : mais pour effectuer le calcul il faut fixer le point de séparation en introduisant sa position angulaire comme donnée : la séparation apparaît alors en un point singulier où la pente est infinie. Le résultat du calcul effectué en fluide parfait démontre les effets inertiels produits par « la pression latérale qui aide la déviation du courant d’air » : la viscosité n’intervient que par l’angle de déviation avant séparation introduit comme une donnée du calcul, et joue un rôle mineur, confirmé par une analyse plus récente[15].

L’image obtenue (au-dessus de la précédente) en introduisant dans ce calcul la déviation globale mesurée pour chaque rapport h/r a été récemment publiée[16] : elle montre un champ de pression très voisin du champ expérimental, l’influence du rapport h/r critique, et la zone à effet Coandă entre deux zones intermédiaires : la différence la plus importante avec l’écoulement réel est que dans ce dernier il n’y a pas de point singulier : la séparation est l’effet sur la couche limite de la remontée de pression, qui n’existe pas dans le jet pariétal sur une paroi plane, et fait apparaître un effet Coandă sur une paroi à rayon supérieur au rayon critique, qui disparaît à un rayon plus petit. Un calcul grossier de couche limite[11] dans le champ de pression calculé en fonction du nombre de Reynolds et du rapport h/r donne l'angle de décollement indiqué sur l'image, voisin de celui mesuré.

Dans le cas d’un jet libre, un champ de pression similaire apparaît entre deux zones symétriques dont les extrémités sont deux points singuliers[16].

Ces résultats partiels datant de soixante ans ont fait l'objet de ce calcul récent, comparé aux mesures de répartitions des pressions ci-dessus. Des mesures supplémentaires seraient souhaitables, ainsi qu'un calcul de couche limite plus élaboré.

Des mesures expérimentales effectuées à basse vitesse ont prouvé que l’effet Coandă ne se produit pas en régime laminaire, et que le rapport critique h/r auquel le jet se sépare sans effet Coandă diminue fortement dans les applications où le nombre de Reynolds Re = Vh/viscosité cinématique est petit : jusqu’à h/r =0,14 si Re = 500, et h/r = 0,05 si Re=100[17].

Si l’espace entourant l’orifice du jet est partiellement fermé par une paroi plane prolongeant l’orifice en formant un angle avec le jet, ou par une suite de facettes, le jet d’abord séparé se réattache plus loin sur la paroi, en emprisonnant une zone tourbillonnaire où un vide partiel causé par l'« entraînement visqueux »[18] maintient une pression inférieure à la pression atmosphérique, suivie d’une surpression au point de réattachement du jet. Si l’angle est inférieur à 25 degrés, la bulle emprisonnée est de dimension négligeable. Si l’angle est supérieur à 65 degrés, le jet ne se réattache pas et n’est pas « coandé », il se sépare parce que sa courbure serait trop grande pour être maintenue par le vide partiel. Le phénomène est analogue à celui du décrochage d'une aile d'avion quand l'incidence augmente. Si l’angle augmente ou diminue entre 30 et 60 degrés, le jet se réattache ou non avec un phénomène d’hystérésis. Cette configuration particulière de jet qui se réattache a fait l’objet d’études très détaillées de la bulle, parce qu’elle autorise la création d’amplificateurs de signaux fluidiques flip-flop de plusieurs types[19], l’écoulement pouvant être bistable.

Des expériences de déviation de jet d’eau par une paroi convexe sont souvent rapportées et la déviation est qualifiée à tort d’« effet Coandă » ; ni Coandă, ni Metral, ni Bouasse, ni Young n’ont fait état d’expériences avec de l’eau, seulement avec de l’air, bien qu'ils aient sans doute remarqué eux aussi que le jet d'eau du robinet suivait la paroi convexe des ustensiles de cuisine et que le liquide coulant d'un récipient dont le bec verseur est trop gros dégouline le long de ce bec. Ce phénomène a été étudié en grand détail par C. Duez et al, qui l'appellent : « effet théière »[20]. En l’absence d’obstacle, une masse d’eau qui débouche dans l’air, quelle que soit sa vitesse initiale, n’est soumise qu’à son propre poids et décrit la même trajectoire que le ferait une masse solide, c’est-à-dire une parabole de tir. Par ailleurs, la tension superficielle de l’eau empêche son mélange avec l’air ambiant, et crée une attraction du jet d’eau par la surface de l’obstacle sur laquelle il vient s’étaler si elle est mouillable. Une pression inférieure à la pression atmosphérique s’installe alors à la paroi de l’obstacle dans des conditions très différentes de celles décrites dans le cas d’un gaz. Si la paroi est convexe, une force d’attraction mutuelle entre l’obstacle et le jet d’eau dévié se produit, perpendiculaire à la paroi, équilibrée selon C. Duez par une force d'adhésion capillaire qui forme un ménisque de raccordement reliant la surface mouillée au jet d'eau. Ce ménisque présente une courbure vers le jet, en sens inverse de celle trouvée par L.C. Woods dans son calcul de l'effet Coandă pour un fluide sans viscosité et sans tension. La déviation d’un jet de liquide par une paroi convexe, « effet théière », est donc produite par des phénomènes radicalement différents de ceux qui produisent la déviation d’un jet de gaz.

L'effet Coandă et l'effet théière sont souvent cités dans des systèmes physiques et mécaniques intervenant dans les organismes vivants, comme au niveau des cordes vocales où l'effet Coandă est modulé lors de la phonation[21] - [22]. L'effet théière s'observe chez le coléoptères « Bombardier » de la sous-famille des Paussinae qui l'utilisent pour guider (par déflexion) les giclées de liquide défensif qu'ils peuvent émettre en jets d'aérosols vers d'éventuels prédateurs[23], ainsi que dans les milieux biologiques, par exemple dans le système sanguin où il pourrait expliquer certains cas de sténose aortique selon French & Guntheroth (1969)[24] - [25].

Divers brevets d'invention basées sur l'effet Coandă ont été déposés par Coandă lui-même[31] puis par d'autres[32] - [33].