Dynamique adaptative
La dynamique adaptative tente d'expliquer les liens entre différents mécanismes : hérédité, mutations et sélection naturelle. Par son aspect mathématique, la dynamique adaptative est un puissant outil pour la compréhension de phénomènes évolutifs passés, présents ou futurs.
Historique
Avant les dynamiques adaptives

Les dynamiques adaptatives sont apparues grâce à l’émergence de plusieurs notions essentielles au cours de l’histoire. Parmi elles, on retrouve la dynamique des populations, c’est-à-dire l’étude de l’évolution de la démographie d’une population dont les fondements sont décrits en 1798 par Thomas Robert Malthus. Son utilisation en biologie permet de prévoir et de comprendre le lien entre écologie et démographie. Ensuite en 1859, Charles Darwin décrit le principe de l’évolution dans son livre L'Origine des espèces. Cette notion s’installe dans le monde scientifique et remplace la théorie du transformisme exposé par Jean-Baptiste Lamarck. Il propose une théorie : celle de la sélection naturelle comme mécanisme principal expliquant l’adaptation des individus dans leur environnement au fil des générations, les individus les mieux "adaptés" étant les plus à même de survivre et de coloniser leur environnement. En 1932, Sewall Wright développe la notion de paysage adaptatif. C’est la représentation graphique d’un phénotype ou caractère en fonction de la valeur sélective. Cette représentation permet de mettre en évidence les différents points d’optimisations du phénotype, appelés aussi points d’équilibres.
Nous observons sur la Figure 1 un paysage adaptatif avec 3 points d’équilibres (A, B, C). Le point d’équilibre B, est le point avec la meilleure valeur sélective pour une variation du trait. L’évolution va tendre à se rapprocher vers ce point d’équilibre B. Ce type de représentation est cependant une représentation fixe de l’évolution alors que l’environnement ne l’est pas. Puis le nouveau mutant modifie à son échelle son environnement. On préfèrera donc une représentation dynamique comme celle de la Figure 2 qui est plus en adéquation avec la réalité.
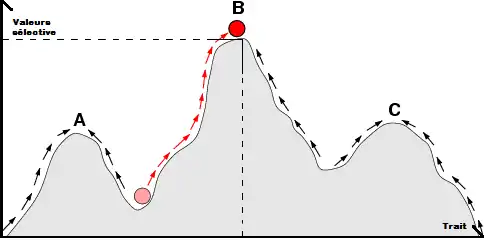
La Figure 2 nous montre la variation de la valeur sélective en fonction du trait. Ici la flèche jaune représente la mutation d'un trait, ce qui va ainsi changer le paysage adaptatif. Ce graphique permet de visualiser la dynamique du paysage adaptatif.
Les dynamiques adaptatives de la théorie des jeux de John Forbes Nash a aussi eu un fort impact sur l’émergence de la dynamique adaptative. En effet, en 1970 cette théorie a permis à John Maynard Smith et d’autre chercheurs de comprendre l’évolution des comportements d’une population face aux variations de son environnement. C’est la "théorie des jeux évolutionnistes". Il émet la notion de Stratégie évolutivement stable (SES ou ESS en anglais pour Evolutionarily stable strategy) qui est reprise dans l’étude des stratégies singulières en dynamique adaptative
L'apparition des dynamique adaptatives
La théorie des dynamiques adaptatives s'est établie de manière empirique dans les années 1990[1]. Les dynamiques adaptatives s'inspirent ainsi des différents outils utilisés en écologie, en particulier la théorie des jeux évolutionnistes et la dynamique des populations, ceci afin d’obtenir une dynamique écologique plus réaliste.
Ces différents domaines soulignent les nombreux aspects des processus évolutifs d’une population. Les dynamiques adaptatives permettent donc de visualiser et de comprendre la conséquence à long terme de petite mutation d'un trait au sein d'une population.
Elle devient un outil puissant pour la modélisation de scénarios évolutifs ou du devenir d'interactions : compétition proies/prédateurs, spéciation, diversification, évolution de coopération, épidémiologie, etc.
Processus stochastiques sous-jacents[2]
L'étude des processus évolutifs comme on le fait en dynamique adaptative doit prendre en compte plusieurs sources de stochasticité.
Premièrement, les processus de mutations qui entraînent l'apparition de nouveaux traits phénotypiques sont ceux qui introduisent la principale source de stochasticité. Pour décrire les propriétés de ces mutations, on introduira donc le facteur μ(x) qui correspond à la fraction de naissances qui donnent lieu à une mutation dans le trait de valeur x. Ces fractions représentent ainsi les probabilités pour qu'un événement de naissance produise un nouveau-né avec un trait de valeur adaptative altérée x'. On ne prend en compte en dynamique adaptative que les mutations pouvant se maintenir dans la population initiale c'est-à-dire la moitié d'entre elles d'où le facteur d'échelle.
Il faut aussi prendre en compte l'impact de la stochasticité environnementale en particulier sur les mutants. En effet les individus d'une population sont des unités discrètes et les mutants sont seuls initialement au sein de la population résidente. Ils sont donc beaucoup plus sensibles aux événements liés à la variabilité de l'environnement . Il faut donc prendre en compte les probabilités pour que les taux de naissance ou de mort b(x, n, t) et d(x, n, t) varient selon le trait étudié mais aussi selon la densité des populations résidentes ou encore selon le temps (qui correspond à la variabilité temporelle comme par exemple l'existence de catastrophes naturelles). Les populations résidentes sont en général moins soumises à cette variabilité que les sous-populations mutantes car elles sont considérées comme assez grande pour que les taux b et d varient peu.
Ces considérations sont d'autant plus importantes en dynamiques coévolutives qui sont une extension des dynamiques adaptatives à 2 espèces en interactions l'une avec l'autre. Dans ces cas les dynamiques des populations des deux espèces sont interdépendantes. L'apparition de mutation pour chaque espèce peut se faire selon des probabilités μ(x) indépendantes et on parle alors de processus de mutations homogènes. Dans le cas où ces probabilités d'apparition d'une mutation dépendent l'une de l'autre, on parlera de populations symétriques.
Équation canonique et hypothèses principales
La “breeder’s equation” proposée en 1937 par Jay Laurence Lush (en), fut aussi un apport majeur pour l’apparition de dynamiques adaptatives puisqu’elle est à la base de l’équation canonique. Historiquement la diversité des phénotypes reflète la diversité des pressions de sélections. La variation (∆x) d’un trait dans la population dépend de son héritabilité h(x), qui est la proportion du trait qui est héritable, du différentiel de sélection qui est la valeur du trait avant et après sélection.
Soit :
Avec Va la variance additive, qui correspond aux effets additifs des allèles et Vp la variance phénotypique.
On a ainsi abouti à partir de l’équation précédente à l’équation canonique de la dynamique adaptative qui est :
Où :
- k(x) le potentiel évolutif de la mutation
- µ(x) et le taux d'apparition des mutations par individu
- σ² la variance phénotypique associée à ces mutations
- N(x) la taille de la population à l'équilibre ayant pour trait phénotypique x
- le gradient de sélection qui indique dans quel sens et avec quelle amplitude le trait x varie à la suite de mutations de petite amplitude.
- ½ facteur d’échelle qui prend en compte que seule la moitié des mutations a un effet sur la variation de x (celles se situant dans la zone positive du gradient de fitness).
Hypothèses en dynamique adaptative
L’équation canonique de la dynamique adaptative se base sur plusieurs hypothèses ce qui permet d’analyser plus facilement les modèles mathématiques utilisés c’est-à-dire les différentes équations de dynamiques de populations qu’on pourrait utiliser. Les principales hypothèses sont les suivantes :
- les échelles de temps écologique et évolutives sont séparées. Les populations sont donc à l'équilibre écologique lorsqu'un mutant apparaît car le taux de mutation est très faible. Ceci implique aussi qu’on ait une séparation temporelle des mutations: deux mutants ne peuvent exister en même temps ni au même endroit : c’est le principe de l’exclusion mutuelle.
- les mutations ont des effets phénotypiques petits (d’où le fait qu’on évalue le gradient de fitness pour x’ = x dans l’équation canonique). En d’autres termes, il n’y a pas de “révolution” dans le trait, la modification du trait mutant est légère par rapport au trait du résident. Ces différents traits phénotypiques peuvent être quantifiables et observables au cours du temps (taille des individus, temps de gestations/différenciations, etc.).
- le mutant est rare quand il apparaît ce qui nous permet de dire que sa densité est négligeable dans l’équation canonique
- les populations sont asexuées, les individus sont considérés haploïdes, c’est-à-dire se reproduisant de façon clonale.
- les densités à l'équilibre sont stables : on ne prendre donc pas en compte l’existence de dynamique cycliques.
Le but est d’observer le devenir de ce mutant rare dans la population. Soit il disparaît, soit il envahit le milieu. En envahissant le milieu le mutant devient le nouveau résident en changeant la valeur de ce trait phénotypique, c'est-à-dire en augmentant sa fitness par rapport au résident
Définition de fitness en dynamique adaptative
La fitness d'un mutant correspond au taux de croissance de ce mutant dans l'environnement fixé par les traits du résident (c'est-à-dire que les densités de populations à l'équilibres sont fixées par les traits du résident).On la notera W telle que :
On notera que la fonction de fitness en temps discret s’écrit W mais qu’en temps continu on la note s. W est sans dimension contrairement à s en temps continu et les deux sont d’ailleurs reliées tel que :
avec dt : l’intervalle de temps sur lequel le modèle en temps discret est basé.
Subtilités
Définir la fitness en population structurée, subdivisée, la fitness diploïde, l’évolution de plusieurs traits ou les régimes de sélection et les cycles de vie apparaissent comme étant des difficultés majeures en formalisation mathématique (ce qui explique l’une des hypothèse de la dynamique adaptative qui est de considérer les populations asexuées). L’idée serait donc de calculer la fitness en tenant compte du temps passé dans chaque stade de vie, de l’espérance de vie, de la fécondité à chaque stade de vie mais aussi du caractère hétérozygote ou homozygote d’un mutant.
En ce qui concerne populations subdivisées ou métapopulations, il faut utiliser un critère de fitness s’appuyant sur la dispersion plutôt que sur la fécondité. Ainsi il faut tenir compte des traits d’histoire de vie des individus et des mutants, mais aussi de la production de mutants dispersants en fonction du nombre de mutants, tout en incluant l’importance de l’apparentement (règle d’Hamilton).
De plus représenter la rareté d’une espèce est plus difficile dans un système structuré spatialement à cause de la définition même de la rareté d’une espèce. Dans l’équation canonique on considérait le mutant comme rare dans la population totale, mais si celle-ci est répartie, la rareté du mutant là où il apparait peut être remis en question selon que l’on a peu d’individus dans plusieurs patchs ou plus d’individus dans un unique patch. De plus, la dynamique des patchs peut être aussi différente entre patchs : croissance dans l’un et décroissance dans l’autre, et peut être fonction du passé de ces patchs[3]. Tout ceci implique des travaux en cours qui tentent de faire des modèles et le choix d’un ordre entre les événements (de reproduction, émigration, immigration, changement environnemental) n’est pas neutre. Un ordre différent peut impliquer une prédiction différente dans un modèle de dynamique adaptative.
Détermination et caractérisation des stratégies évolutives singulières
En dynamique adaptative on se place dans une population à l’équilibre et isolée, c’est la population résidente N. Les phénotypes sont les traits quantitatifs individuels héritables, les naissances et les morts sont déterminées par le phénotype et par l’environnement (celui-ci étant constitué par le reste de la population ainsi que par les facteurs externes).
En dynamique adaptative on observe donc l'apparition d'une mutation pour un trait donné conduisant a une fitness invasive (fonction d'invasion) évoluant dans la population donnée par l’équation canonique .
On doit déterminer les paramètres caractérisant le résident et ceux caractérisant le mutant, on écrit donc les équations des dynamique de la sous population résidente N et de la population mutante N'
On a donc pour la population résidente :
(1)
Et pour la population mutante :
(2)
Or comme N et N' coexistent dans le même milieu fermé et que N'≪N car le mutant est rare, on peut simplifier les équations par en remplaçant dans (1) et (2)
Pour le résident on a :
Et pour le mutant :
On se place à l’équilibre de population soit : donc
On peut ensuite calculer le taux d’accroissement d’un mutant rare à partir de (2)
Cette formule est le taux d’accroissement de la sous population mutante N' et permet d’exprimer la fitness (s) du mutant dans la population résidente N. La dérivée partielle de la fitness par rapport au trait x' permet de déterminer un gradient de sélection.
Si x' augmente. On observe une invasion de x'.
Si x' diminue. Le mutant x' va disparaître.
Si et si
alors il s’agit d’une stratégie évolutivement stable (Evolutionary Stable Strategy). x' se maintient mais n'envahit pas complètement la population.
Outils graphiques
Approche par les PIP[4]
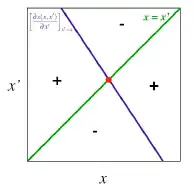
Étant donné la complexité des modèles utilisés en dynamique adaptatives on peut s’aider d’outils graphiques comme les Diagrammes d’Invasions Binaires ou PIP (Pairwise Invasibility Plots).En connaissant la fonction de fitness et ses paramètres qui la définissent on peut déterminer graphiquement les évolutifs de notre dynamique. Sur ces diagrammes on représente en abscisse la valeur du trait x et en ordonnée la valeur du trait x’. On représente ensuite deux courbes: la bissectrice qui n’est autre que la droite d’équation x = x’ et la courbe isocline qui correspond à notre gradient de sélection (on a ici une droite mais ce n’est pas toujours le cas. Le signe de chaque zone est déterminé par le signe du gradient de sélection et correspond donc au caractère invasible ou non du trait x’.
Chaque intersection entre les 2 courbes correspond à une stratégie singulière c’est-à-dire à un équilibre x* là où le gradient de sélection s’annule comme dans l’approche mathématique.
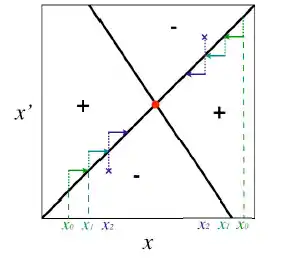
Comme on l’a expliqué, les régions positives représentent la combinaison de trait (x ; x’) pour laquelle le mutant avec le trait x’ peut envahir la population résidente qui possède le trait x ; À l’inverse, les régions négative représente la combinaison de trait pour laquelle un mutant avec le trait x’ ne peut pas envahir le milieu et ainsi disparaît. On peut ainsi déterminer le caractère invasible ou non de la stratégie singulière en regardant dans quelques zones se situent les valeurs de x’. Pour la Figure 4. par exemple à x*, quelles que soient les valeurs de x’ on se trouve dans une région négative, l’équilibre et donc stable et le mutant ne peut pas envahir la population.
On peut ensuite étudier la convergence de la dynamique vers cet équilibre en prenant des valeurs x0 et x’0 dans les régions positives et on regarde ensuite dans quelle direction va l’invasion par le mutant. On répète ceci en prenant de nouvelles valeurs (de x0 en x2). Si on se dirige vers l’équilibre, alors la dynamique est convergente si on va dans le sens inverse, alors elle est non convergente.Toujours dans la Figure 4 on voit que dans les deux cas de régions positives (X’ > Xn et X’ < Xn) la population de mutant x’ converge vers l’équilibre x* . On a donc dans cet exemple un équilibre stable et convergent et donc une stratégie continuellement stable (CSS). On retrouve donc les résultats obtenus par l’approche mathématique.
On retrouve différents types de graphiques PIP, chacun ayant sa particularité, expliquant les différentes possibilités d’évolutions d’un mutant.
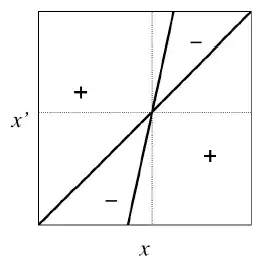
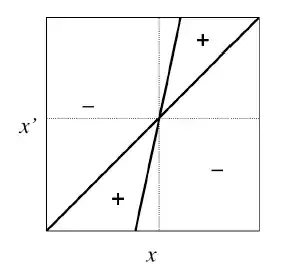
Dans un scénario évolutif de type Jardin d'Eden (Figure 5), on a un point d’équilibre stable mais non convergent. L’équilibre ne peut donc pas être atteint bien qu’il représente un idéal évolutif du point de vue de ce trait et l’évolution ira dans le sens d’un éloignement de cet équilibre. Le fait que l’équilibre pour un trait donné ne peut être atteint peut traduire l’effet de conflits évolutifs entre niveaux de sélection notamment l’impact contraintes évolutives d’autres traits sur le trait étudié.
Dans un scénario de type branchement évolutif (Figure 6), on a un équilibre stable et convergent. Cela signifie qu’une fois l’équilibre atteint des mutants peuvent apparaître et avoir des taux de croissances positifs. Ils pourraient ainsi potentiellement coexister et former de nouvelles populations avec des phénotypes différents (voir en s’isolant former de nouvelles espèces) . C’est ce qu’on appelle un point de branchement évolution qui pourrait expliquer théoriquement la spéciation de type sympatrique même si les conséquences réelles sur les populations sont encore débattues. La figure 7, récapitule les différents cas de PIP selon la stabilité de l'équilibre et sa convergence.

Approche en modélisation
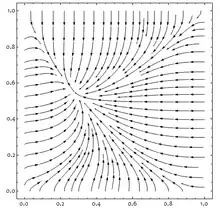
Afin de formaliser un modèle de dynamique adaptative, la communauté scientifique a souvent recours à des logiciels de formalisation mathématique comme Mathematica, des logiciels de traitement de données et d’analyses statistiques comme le logiciel R. Ces logiciels permettent à la fois d’écrire les modèles et de les confronter à la réalité biologiques afin d’établir des prédictions quant à la dynamique des populations étudiées.
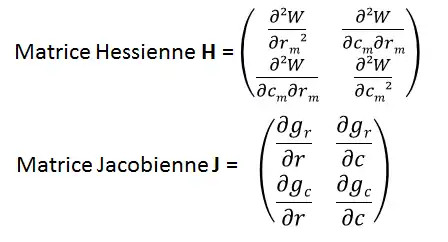
L’exemple pris est ici un modèle étudiant le trade-off résistance aux perturbations r et taux de colonisation c. À partir de la fonction d’invasion du mutant rare (: fitness), on peut calculer les gradients de sélection sur ces deux paramètres (r et c) en dérivant la fonction de fitness. Les dérivées de ses gradients donnant deux matrices : la matrice Hessienne et la matrice Jacobienne (Figure 7). Ces matrices permettent de connaître si l’équilibre (visualisé Figure 6) correspond à une stratégie évolutivement stable (ESS), à un point de branchement, un repoussoir ou s’il est convergent stable.
Exemple : Évolution du temps d’arrivée des oiseaux [5]
Ce modèle décrit comment appliquer les dynamiques adaptatives sur des modèles en temps discret. Il décrit l’évolution du temps d’arrivée des oiseaux dans leurs sites de nichées. Une arrivée précoce réduit la valeur reproductive des individus adultes en les soumettant à des conditions sévères encore proches de celles de l’hiver. À l’inverse, avec une arrivée retardée, les oiseaux risquent de manquer le pic d’abondance de larves d’insectes pour leurs jeunes. On pourrait penser que l’évolution provoquerait l’arrivée de tous les oiseaux au temps optimal pour la population mais ce modèle montre que la compétition pour les sites de nichées entraine l’arrivée de certains oiseaux plus tôt, malgré le fait que les conditions soient dures.
La question est donc : quand les oiseaux doivent-ils arriver pour maximiser leur valeur reproductive (c’est-à-dire leur fitness d’une manière plus générale)?
Tout d’abord on définit la dynamique pour la population résidente :
Avec
- x : le temps d’arrivée d’une population résidente d’oiseaux migratoires
- K : le nombre de sites de nichées disponible tel que sinon il n’existe pas de compétition. Celle-ci est supposée intense puisque rater l’occasion d’avoir un site de nichée signifie ne pas se reproduire cette année pour ces oiseaux.
- R(x): le nombre de descendants par individu (qui traduit la capacité reproductive de l’individu)
- p : la probabilité d’un individu de survivre d’une année sur l’autre.
On trouve donc à l’équilibre (quand donc à . C’est un équilibre stable sachant que le temps pour lequel on maximise la taille de la population est On considère maintenant une invasion par un mutant dont la taille de population est donnée par n’t (mais initialement rare dans la population) et avec un temps d’arrivée x’. Ce qui nous donne :
Avec C(x): la capacité de compétition d’un individu (dans ce cas on regarde la capacité de l’individu à protéger son territoire). Comme on peut le voir dans ces équations, une compétition s’est mise en place entre les individus résidents et les individus mutants puisqu’il y a une différence de fitness concernant le trait ou plutôt la stratégie « temps d’arrivée » ce qui n’était pas le cas dans la population uniquement constituée de résident puisqu’ils avaient tous la même valeur pour ce trait.
Pour reprendre les observations faites sur la population d’oiseaux, on supposera que la fonction C(x)décrivant la capacité de compétition en fonction du temps d’arrivée diminue de façon exponentielle. De la même manière la fonction R(x) suit une fonction gaussienne avec un nombre de descendants maximal au (ou plutôt un nombre maximal élevés dans de meilleures conditions et donc avec de meilleures chances de survie)
Étant donné que l’on travaille en temps discret, on notera la fonction de fitness comme le taux de croissance annuel (taux de croissance géométrique) d’un mutant initialement rare. On notera que la fonction de fitness en temps discret est sans dimension contrairement à s en temps continu ; Les deux sont d’ailleurs reliées tel que
avec Δt : l’intervalle de temps sur lequel le modèle en temps discret est basé.
On refait donc les mêmes hypothèses des dynamiques adaptatives à savoir que les résidents sont largement majoritaires et que le mutant est initialement si rare qu’il a une influence négligeable sur le taux de croissance par individu. On a donc :
Comme on a l’a vu avec les modèles en temps continu, ceci n’est valable que si on considère la population résidente comme étant à l’équilibre ce qui en temps discret correspond à On détermine ensuite le gradient de sélection via la dérivée partielle de la fonction de fitness par rapport au trait x', et on obtient :
Une arrivée tardive est donc favorisée lorsque la décroissance de la capacité de compétition est petite par rapport à la décroissance du succès reproducteur . On voit ainsi que la sélection entraîne un compromis entre la nécessité de sécuriser un territoire et la volonté de maximiser son nombre de descendants.
Pour la suite des calculs on pose qui correspondent respectivement à des fonctions exponentielles décroissantes et gaussiennes. Le gradient de sélection et linéaire et décroît. Il y a donc une seule stratégie évolutive qui doit être convergente et stable.
On résout donc l’équation ce qui nous donne .
De plus on peut voir par calcul que donc l’équilibre x* est convergent, on a donc une stratégie évolutive continuellement stable (CSS).
On peut donc conclure qu’en raison de l’avantage individuel d’arriver plus tôt, relativement au reste de la population, la stratégie la plus stable évolutivement se situe un peu avant la date d’arrivée qui maximise la taille de la population. C’est un exemple de la Tragédie des biens communs en évolution. Les intérêts du groupe (avoir une population maximale) sont en conflit avec les intérêts de l’individu que traduit l’ESS.
Références
- Stéphane Génieys, Vitaly Volpert, Pierre Auger, Adaptive dynamics: modelling Darwin’s divergence principle, Comptes Rendus Biologies, 2006
- Dieckmann, U, et R Law, The Dynamical Theory of Coevolution: A Derivation from Stochastic Ecological Processes, J. Math. Biol. 34, 1996.
- François Massol, The metapopulation fitness criterion : Proof and perspective by François Massol, Theoretical Population Biology, Volume 75, 2009
- Odo Diekmann, A beginner’s guide to adaptative dynamic, Banach Center Publications, volume 63, 2004
- Åke Brännström, Jacob Johansson and Niels von Festenberg, The Hitchhiker’s Guide to Adaptive Dynamics, Games, 2013

![{\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}=k(x)N(x)\left[{\frac {\partial s}{\partial x^{'}}}\right]_{(x^{'}=x)}}](https://img.franco.wiki/i/5a423c3885ede429e7f18d1f7404d7c682d78509.svg)

![{\displaystyle \left[{\frac {\partial s}{\partial x^{'}}}\right]_{(x^{'}=x)}}](https://img.franco.wiki/i/b866bca701f537cc93836f4b14a5200e6039a991.svg)
![{\displaystyle W(x,x')={\frac {1}{\mathrm {N} '}}\left({\frac {\mathrm {d} N'}{\mathrm {d} t}}\right)_{([x=x'])}}](https://img.franco.wiki/i/45315450476e7f7bfefdcdd8df78ff322ebaeb66.svg)































