En analyse statistique, le problème de détection de ruptures (ou détection de points de changement) est un problème de régression ayant pour but d'estimer les instants où un signal présente des changements dans la distribution. Ces instants sont matérialisés sur les deux figures par des lignes verticales bleues. Classiquement, on réalise de la détection de rupture pour un signal ayant des changements dans la moyenne. De manière plus générale, on réalise de la détection de ruptures pour un signal ayant des changements dans la distribution (par exemple, dans la moyenne et la variance).
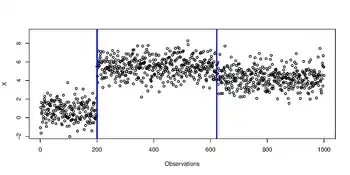
Exemple de signal ayant des changements dans la moyenne.
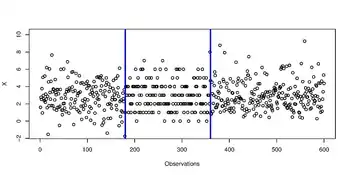
Exemple de signal ayant des changements dans la distribution.
La détection de ruptures peut s'appliquer à un signal sonore d'une émission dont on souhaite estimer les instants où l'on change de situations, à la détection d'attaques informatiques (variations de flux réseaux)[1], ou encore au contrôle qualité.
Cet article traite du problème de détection de ruptures rétrospective (dite offline) où l'on dispose de l'ensemble des données du signal. Ce contexte est différent d'une détection temps réel (dite online) où les données du signal arrivent à la volée, mais moins à même de détecter précisément l'instant de rupture.
Soit ![{\displaystyle \{X_{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/2807f2f8e2582fca40f9ce6389afbce7bb6f8917.svg) un signal réel, provenant d'observations recueillies au cours des instants
un signal réel, provenant d'observations recueillies au cours des instants  , présentant des changements dans la distribution. En notant
, présentant des changements dans la distribution. En notant  la loi de probabilité de
la loi de probabilité de  , la distribution de
, la distribution de ![{\displaystyle \{X_{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/2807f2f8e2582fca40f9ce6389afbce7bb6f8917.svg) vérifie :
vérifie :

avec  étant les vrais instants de ruptures (on note
étant les vrais instants de ruptures (on note  (
( est le vrai nombre de segments) avec la convention
est le vrai nombre de segments) avec la convention  et
et  ). On cherche à estimer ces instants de ruptures à l'aide d'un algorithme.
). On cherche à estimer ces instants de ruptures à l'aide d'un algorithme.
Dans le cas de la détection de rupture dans la moyenne, le modèle est :
![{\displaystyle {\begin{aligned}\forall t\in [\![1,T]\!],~X_{t}=s_{t}+\epsilon _{t},\end{aligned}}}](https://img.franco.wiki/i/f9d7f225e35d239141ab112fd2e21205bc34040f.svg)
avec ![{\displaystyle \{s_{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/945ed905c7e82b70060c975315d01a1cd55f87f3.svg) est la fonction de régression et
est la fonction de régression et ![{\displaystyle ~\{\epsilon _{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/e50e38b0c17a3c6cf895d608a6359deca110208d.svg) est un bruit d'espérance nulle et de variance
est un bruit d'espérance nulle et de variance  . La fonction de régression
. La fonction de régression ![{\displaystyle \{s_{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/945ed905c7e82b70060c975315d01a1cd55f87f3.svg) est supposée constante par morceaux avec des discontinuités à chaque vrai instant de ruptures
est supposée constante par morceaux avec des discontinuités à chaque vrai instant de ruptures ![{\displaystyle \{\tau _{i}^{*}\}_{i\in [\![0,D^{*}]\!]}}](https://img.franco.wiki/i/97c8030397be9ea0877a3b94647dd248356f551e.svg) .
.
Dans le cas de la détection de ruptures dans la distribution, on recode les observations initiales ![{\displaystyle \{X_{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/2807f2f8e2582fca40f9ce6389afbce7bb6f8917.svg) par de nouvelles observations
par de nouvelles observations ![{\displaystyle \{Y_{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/d6232bcf3e7e8088ad01f4f91e5bbbc35a256f13.svg) définies par
définies par  où
où  est un noyau symétrique et semi-défini positif (en) (par exemple
est un noyau symétrique et semi-défini positif (en) (par exemple  :
:  est le noyau linéaire ; autre exemple
est le noyau linéaire ; autre exemple  :
:  est le noyau Gaussien de paramètre
est le noyau Gaussien de paramètre  ). Pour un noyau symétrique et semi-défini positif
). Pour un noyau symétrique et semi-défini positif  , le théorème de Moore-Aronszahn assure l'existence d'un espace de Hilbert à noyau reproduisant
, le théorème de Moore-Aronszahn assure l'existence d'un espace de Hilbert à noyau reproduisant  de noyau reproduisant
de noyau reproduisant  .
.
Le modèle est :
![{\displaystyle {\begin{aligned}\forall t\in [\![1,T]\!],~Y_{t}=\mu _{t}^{*}+\epsilon _{t},\end{aligned}}}](https://img.franco.wiki/i/2b2dba72660f768c239a5d9d7fcee70088124508.svg)
avec ![{\displaystyle \{\mu _{t}^{*}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/3b3eb11dd6bc2cc8204f51d2ef77f4b775f4d7bd.svg) est la fonction de régression et
est la fonction de régression et ![{\displaystyle ~\{\epsilon _{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/e50e38b0c17a3c6cf895d608a6359deca110208d.svg) est un bruit d'espérance nulle et de variance
est un bruit d'espérance nulle et de variance  . De plus,
. De plus, ![{\displaystyle \forall t\in [\![1,T]\!],~Y_{t},~\mu _{t}^{*},~\epsilon _{t}}](https://img.franco.wiki/i/d5e046562675572f5919299013e963e013ab0cda.svg) appartiennent à
appartiennent à  . La fonction de régression
. La fonction de régression ![{\displaystyle \{\mu _{t}^{*}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/3b3eb11dd6bc2cc8204f51d2ef77f4b775f4d7bd.svg) est supposée constante par morceaux avec des discontinuités à chaque vrai instant de ruptures
est supposée constante par morceaux avec des discontinuités à chaque vrai instant de ruptures ![{\displaystyle \{\tau _{i}^{*}\}_{i\in [\![0,D^{*}]\!]}}](https://img.franco.wiki/i/97c8030397be9ea0877a3b94647dd248356f551e.svg) .
.
Méthodes existantes
Le problème de détection de ruptures peut être vu comme un problème de sélection de modèle[2]: chaque segmentation candidate (i.e. liste d'instants de ruptures candidats) est reliée à un modèle qu'il faut choisir. Nous présentons deux approches : l'une utilisant le principe de la programmation dynamique et l'autre l'heuristique de segmentation binaire dans le cadre classique de la détection de ruptures dans la moyenne puis dans le cas général de la détection de ruptures dans la distribution. Pour chacune de ces deux méthodes, nous présentons les algorithmes permettant de calculer une segmentation en  segments
segments  optimisant un critère (ici, le risque empirique).
optimisant un critère (ici, le risque empirique).
Notations
Nous présentons les notations communes aux deux méthodes puis celles qui leur sont spécifiques :
Notation commune
 l'ensemble des segmentions
l'ensemble des segmentions  en
en  segments
segments  .
.
Notations pour le cas de la détection de ruptures dans la moyenne
 et
et  .
. :
:  est l'ensemble des vecteurs
est l'ensemble des vecteurs  constants par morceaux sur les segments de
constants par morceaux sur les segments de  .
.- Estimateur du risque empirique :
 .
.
Notations pour le cas de la détection de ruptures dans la distribution
 et
et  .
. pour
pour  avec
avec ![{\displaystyle (s,e)\in [\![1,T]\!]^{2}}](https://img.franco.wiki/i/15bea1f21b555f22e8680df542c09ffece3ac699.svg) .
. :
:  est l'ensemble des vecteurs
est l'ensemble des vecteurs  constants par morceaux sur les segments de
constants par morceaux sur les segments de  .
.- Norme dans
 :
:  .
.
- Estimateur du risque empirique :
 .
.
Les méthodes proposées ci-dessous utilisent le risque empirique comme critère à minimiser ( pour la détection de ruptures dans la moyenne ;
pour la détection de ruptures dans la moyenne ;  pour la détection de ruptures dans la distribution). Pour le noyau linéaire
pour la détection de ruptures dans la distribution). Pour le noyau linéaire  ,
,
 , les méthodes utilisées dans le cadre classique se déduisent de celles du cas des noyaux par le biais de
, les méthodes utilisées dans le cadre classique se déduisent de celles du cas des noyaux par le biais de  : donc on ne présentera les algorithmes que dans le cas des noyaux.
: donc on ne présentera les algorithmes que dans le cas des noyaux.
Programmation dynamique
La méthode de la programmation dynamique utilise le principe d'optimalité de Bellman : toute solution optimale s'appuie elle-même sur des sous-problèmes résolus localement de façon optimale. On utilise cette méthode exacte pour récupérer pour ![{\displaystyle D\in [\![1,D_{max}]\!]}](https://img.franco.wiki/i/ee89e6552cc00e3c25097979019ee906c86b610f.svg) la meilleure segmentation en
la meilleure segmentation en  segments minimisant le risque empirique i.e. :
segments minimisant le risque empirique i.e. :

Nous présentons dans cette section l'algorithme de programmation dynamique appliquée au problème de détection de ruptures[3] - [4]. Dans un premier temps, nous exprimons le risque empirique  en fonction du noyau
en fonction du noyau  et de
et de ![{\displaystyle \{X_{i}\}_{i\in [\![1,T]\!]}}](https://img.franco.wiki/i/5794c2592c56173dcbad0ae038bda685c80b6fec.svg) à l'aide des deux résultats suivants ci-dessous.
à l'aide des deux résultats suivants ci-dessous.
On montre tout d'abord que, pour ![{\displaystyle m\in {\mathcal {M}}(D),~d\in [\![1,D-1]\!]}](https://img.franco.wiki/i/318f9fff2ca9b27992c459ba8ba927c5c58d4a95.svg) , pour
, pour ![{\displaystyle i\in [\![\tau _{d},\tau _{d+1}-1]\!]}](https://img.franco.wiki/i/24e86b9cbc5e6c92650f03e8ca1e3a0341cad058.svg) ,
,  .
.
Démonstration
Pour  , notons, pour
, notons, pour  ,
,  la valeur commune de
la valeur commune de  et, pour
et, pour  ,
,  ,
,
Pour  ,
,
![{\displaystyle {\begin{aligned}\|u-g\|_{{\mathcal {H}}^{T}}^{2}&=\sum _{\lambda \in m}\sum _{i\in \lambda }\|u_{\lambda }-g_{i}\|_{\mathcal {H}}^{2}\\&=\sum _{\lambda \in m}\sum _{i\in \lambda }\left[\|u_{\lambda }-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2}+\|g_{i}-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2}+2<u_{\lambda }-{\overline {g}}_{\lambda },{\overline {g}}_{\lambda }-g_{i}>_{\mathcal {H}}\right]\\&=\sum _{\lambda \in m}\left[\mathrm {card} (\lambda )\|u_{\lambda }-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2}\right]+\sum _{\lambda \in m}\sum _{i\in \lambda }\|g_{i}-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2}+2\sum _{\lambda \in m}<u_{\lambda }-{\overline {g}}_{\lambda },\sum _{i\in \lambda }({\overline {g}}_{\lambda }-g_{i})>_{\mathcal {H}}\\&=\sum _{\lambda \in m}\left[\mathrm {card} (\lambda )\|u_{\lambda }-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2}\right]+\sum _{\lambda \in m}\sum _{i\in \lambda }\|g_{i}-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2},\end{aligned}}}](https://img.franco.wiki/i/7cc4687144001fafc36c403cfc392725fb79266c.svg)
Ainsi,  est minimale si et seulement si
est minimale si et seulement si  pour chaque
pour chaque  .
.
On montre que, pour  ,
,
![{\displaystyle {\begin{aligned}\|Y-{\hat {\mu }}_{m}\|_{{\mathcal {H}}^{T}}^{2}=\sum _{d\in [\![1,D-1]\!]}C_{\tau _{d},\tau _{d+1}},\end{aligned}}}](https://img.franco.wiki/i/9d487d5efc161c2bf77fd72e126763931f82d7f6.svg)
avec, pour ![{\displaystyle ~(\tau ,\tau ^{'})\in [\![1,T]\!]^{2},~\tau <\tau ^{'}}](https://img.franco.wiki/i/7df2d901b5a831ce553fb06ead4fe55b6525c0b7.svg) ,
, 
Démonstration
![{\displaystyle {\begin{aligned}\|Y-{\hat {\mu }}_{m}\|_{{\mathcal {H}}^{T}}^{2}&=\sum _{d\in [\![1,D-1]\!]}\sum _{i\in [\![\tau _{d},\tau _{d+1}-1]\!]}\|Y_{i}-\left({\hat {\mu }}_{m}\right)_{i}\|_{\mathcal {H}}^{2}\\&=\sum _{d\in [\![1,D-1]\!]}\sum _{i\in [\![\tau _{d},\tau _{d+1}-1]\!]}\left[\|Y_{i}\|_{\mathcal {H}}^{2}+\|{\frac {1}{\tau _{d+1}-\tau _{d}}}\sum _{j=\tau _{d}}^{\tau _{d+1}-1}Y_{j}\|_{\mathcal {H}}^{2}-2<Y_{i},{\frac {1}{\tau _{d+1}-\tau _{d}}}\sum _{j=\tau _{d}}^{\tau _{d+1}-1}Y_{j}>_{\mathcal {H}}\right]\\&=\sum _{d\in [\![1,D-1]\!]}\left(\sum _{i\in [\![\tau _{d},\tau _{d+1}-1]\!]}\|Y_{i}\|_{\mathcal {H}}^{2}-{\frac {1}{\tau _{d+1}-\tau _{d}}}\sum _{i=\tau _{d}}^{\tau _{d+1}-1}\sum _{j=\tau _{d}}^{\tau _{d+1}-1}<Y_{i},Y_{j}>_{\mathcal {H}}\right)\\&=\sum _{d\in [\![1,D-1]\!]}\left(\sum _{i=\tau _{d}}^{\tau _{d+1}-1}k(X_{i},X_{i})-{\frac {1}{\tau _{d+1}-\tau _{d}}}\sum _{i=\tau _{d}}^{\tau _{d+1}-1}\sum _{j=\tau _{d}}^{\tau _{d+1}-1}k(X_{i},X_{j})\right)\\&=\sum _{d\in [\![1,D-1]\!]}C_{\tau _{d},\tau _{d+1}}.\end{aligned}}}](https://img.franco.wiki/i/a4c3ee39d603c59dec2ca4ce7c2c25a4816d13d7.svg)
KPGD est l'implémentation du principe de la programmation dynamique à noyau
appliquée au problème de détection de ruptures. Elle prend en paramètre la matrice de coût ![{\displaystyle C=(C_{i,j})_{(i,j)\in [\![1,T]\!]}(i<j)}](https://img.franco.wiki/i/968ecda021a68c0af7c0a2b040dc94279f350eb0.svg) et elle renvoie
et elle renvoie ![{\displaystyle \{{\hat {m}}_{D}\}_{D\in [\![1,D_{max}]\!]}}](https://img.franco.wiki/i/459f103b241f13f0e2f1d73c5b9f1f219b04753c.svg) .
.
algorithme KPGD ( )
for
)
for ![{\displaystyle d\in [\![2,D_{max}]\!]}](https://img.franco.wiki/i/7d59c1a388024e8815f605b13dd6a7eb06dc513d.svg) do
for
do
for ![{\displaystyle \tau ^{'}\in [\![d,T]\!]}](https://img.franco.wiki/i/c63c9817c704450063627d2e37b7a3df170988ee.svg) do
do

 end for
end for
Fin algorithme
end for
end for
Fin algorithme
avec  .
.
La sélection de modèle[4] permet de récupérer  un estimateur du nombre de segments
un estimateur du nombre de segments  .
.
 est défini par
est défini par
![{\displaystyle {\begin{aligned}{\hat {D}}={\underset {D\in [\![1,D_{max}]\!]}{\operatorname {arg\,min} }}\{\|Y-{\hat {\mu }}_{{\hat {m}}_{D}}\|_{{\mathcal {H}}^{T}}^{2}+pen({\hat {m}}_{D})\},\end{aligned}}}](https://img.franco.wiki/i/3124df24e24d111d1a42caf3259b18d5f95b0e9e.svg)
avec  . La méthode utilisée pour calibrer la constante
. La méthode utilisée pour calibrer la constante  est l'heuristique de pente[5]. On obtient ainsi un estimateur
est l'heuristique de pente[5]. On obtient ainsi un estimateur  .
.
Segmentation binaire
L'heuristique de segmentation binaire[6] est une méthode, fonctionnant par dichotomie, permettant de récupérer un minimiseur local  du risque empirique
du risque empirique  . Plus précisément, la segmentation binaire cherche à la première itération l'indice
. Plus précisément, la segmentation binaire cherche à la première itération l'indice ![{\displaystyle j_{1}\in [\![2,T-1]\!]}](https://img.franco.wiki/i/15af2b7f12af2cb5586ea7fbdc5223878b54d562.svg) de l'instant de ruptures candidat qui minimise le risque empirique
de l'instant de ruptures candidat qui minimise le risque empirique  : cet indice est l'indice de notre premier instant de ruptures estimé. Puis, elle détermine récursivement, à la deuxième itération, deux instants de ruptures candidats
: cet indice est l'indice de notre premier instant de ruptures estimé. Puis, elle détermine récursivement, à la deuxième itération, deux instants de ruptures candidats  sur chacun des segments délimités par les instants de ruptures estimés. Elle retient comme second instant de ruptures estimé celui (parmi ces deux instants de ruptures candidats) qui minimisent le risque empirique. Puis, on procède de la même manière pour les itérations suivantes. Nous illustrons sur un exemple le fonctionnement de l'algorithme utilisant le principe de la segmentation binaire :
sur chacun des segments délimités par les instants de ruptures estimés. Elle retient comme second instant de ruptures estimé celui (parmi ces deux instants de ruptures candidats) qui minimisent le risque empirique. Puis, on procède de la même manière pour les itérations suivantes. Nous illustrons sur un exemple le fonctionnement de l'algorithme utilisant le principe de la segmentation binaire :
- Étape 1 : A l'itération
 , on cherche
, on cherche  qui minimise le risque empirique
qui minimise le risque empirique  avec
avec  pour
pour ![{\displaystyle j\in [\![2,T-1]\!]}](https://img.franco.wiki/i/4e7cdfca712cad41aceb60021cafb9552372afbb.svg) avec :
avec :

 est notre premier instant de ruptures estimé noté
est notre premier instant de ruptures estimé noté  .
.
- Étape 2 : A l'itération on
 , on cherche
, on cherche  minimisant le risque empirique sur
minimisant le risque empirique sur ![{\displaystyle [\![2,{\hat {\tau }}_{1}-1]\!]}](https://img.franco.wiki/i/34f3e1ae2e5fa3007ee11b12265ce547383e7a7c.svg) et
et ![{\displaystyle [\![{\hat {\tau }}_{1}+1,T-1]\!]}](https://img.franco.wiki/i/b202a6ba98dade00ad10f8af91a0e6d4ff60b636.svg) respectivement. Par exemple,
respectivement. Par exemple,
![{\displaystyle j_{2}={\underset {j\in [\![2,{\hat {\tau }}_{1}-1]\!]}{\operatorname {arg\,min} }}\|Y_{1}^{{\hat {\tau }}_{1}}-{\hat {\mu }}_{m_{2}}\|_{{\mathcal {H}}^{{\hat {\tau }}_{1}}}^{2},}](https://img.franco.wiki/i/67c225fa326461c798ceaecf84195ce277ed7626.svg)
avec  . Puis on choisit parmi les instants de ruptures candidats
. Puis on choisit parmi les instants de ruptures candidats  celui qui minimise le risque empirique
celui qui minimise le risque empirique 
et on le note  . Puis, on continue récursivement.
. Puis, on continue récursivement.
Ainsi, au bout de  itérations, on récupère une segmentation en
itérations, on récupère une segmentation en  segments vérifiant :
segments vérifiant :

avec  l'espace des segmentations en
l'espace des segmentations en  segments où les instants de ruptures estimés
segments où les instants de ruptures estimés  ont été calculés aux itérations précédentes.
ont été calculés aux itérations précédentes.
Une méthode alternative de segmentation binaire avec temps d'arrêt[7] permet d'estimer le nombre de segments et donc de récupérer un estimateur  de
de  .
.


![{\displaystyle \{X_{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/2807f2f8e2582fca40f9ce6389afbce7bb6f8917.svg)









![{\displaystyle {\begin{aligned}\forall t\in [\![1,T]\!],~X_{t}=s_{t}+\epsilon _{t},\end{aligned}}}](https://img.franco.wiki/i/f9d7f225e35d239141ab112fd2e21205bc34040f.svg)
![{\displaystyle \{s_{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/945ed905c7e82b70060c975315d01a1cd55f87f3.svg)
![{\displaystyle ~\{\epsilon _{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/e50e38b0c17a3c6cf895d608a6359deca110208d.svg)

![{\displaystyle \{\tau _{i}^{*}\}_{i\in [\![0,D^{*}]\!]}}](https://img.franco.wiki/i/97c8030397be9ea0877a3b94647dd248356f551e.svg)
![{\displaystyle \{Y_{t}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/d6232bcf3e7e8088ad01f4f91e5bbbc35a256f13.svg)








![{\displaystyle {\begin{aligned}\forall t\in [\![1,T]\!],~Y_{t}=\mu _{t}^{*}+\epsilon _{t},\end{aligned}}}](https://img.franco.wiki/i/2b2dba72660f768c239a5d9d7fcee70088124508.svg)
![{\displaystyle \{\mu _{t}^{*}\}_{t\in [\![1,T]\!]}}](https://img.franco.wiki/i/3b3eb11dd6bc2cc8204f51d2ef77f4b775f4d7bd.svg)
![{\displaystyle \forall t\in [\![1,T]\!],~Y_{t},~\mu _{t}^{*},~\epsilon _{t}}](https://img.franco.wiki/i/d5e046562675572f5919299013e963e013ab0cda.svg)
















![{\displaystyle (s,e)\in [\![1,T]\!]^{2}}](https://img.franco.wiki/i/15bea1f21b555f22e8680df542c09ffece3ac699.svg)









![{\displaystyle D\in [\![1,D_{max}]\!]}](https://img.franco.wiki/i/ee89e6552cc00e3c25097979019ee906c86b610f.svg)

![{\displaystyle \{X_{i}\}_{i\in [\![1,T]\!]}}](https://img.franco.wiki/i/5794c2592c56173dcbad0ae038bda685c80b6fec.svg)
![{\displaystyle m\in {\mathcal {M}}(D),~d\in [\![1,D-1]\!]}](https://img.franco.wiki/i/318f9fff2ca9b27992c459ba8ba927c5c58d4a95.svg)
![{\displaystyle i\in [\![\tau _{d},\tau _{d+1}-1]\!]}](https://img.franco.wiki/i/24e86b9cbc5e6c92650f03e8ca1e3a0341cad058.svg)







![{\displaystyle {\begin{aligned}\|u-g\|_{{\mathcal {H}}^{T}}^{2}&=\sum _{\lambda \in m}\sum _{i\in \lambda }\|u_{\lambda }-g_{i}\|_{\mathcal {H}}^{2}\\&=\sum _{\lambda \in m}\sum _{i\in \lambda }\left[\|u_{\lambda }-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2}+\|g_{i}-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2}+2<u_{\lambda }-{\overline {g}}_{\lambda },{\overline {g}}_{\lambda }-g_{i}>_{\mathcal {H}}\right]\\&=\sum _{\lambda \in m}\left[\mathrm {card} (\lambda )\|u_{\lambda }-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2}\right]+\sum _{\lambda \in m}\sum _{i\in \lambda }\|g_{i}-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2}+2\sum _{\lambda \in m}<u_{\lambda }-{\overline {g}}_{\lambda },\sum _{i\in \lambda }({\overline {g}}_{\lambda }-g_{i})>_{\mathcal {H}}\\&=\sum _{\lambda \in m}\left[\mathrm {card} (\lambda )\|u_{\lambda }-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2}\right]+\sum _{\lambda \in m}\sum _{i\in \lambda }\|g_{i}-{\overline {g}}_{\lambda }\|_{\mathcal {H}}^{2},\end{aligned}}}](https://img.franco.wiki/i/7cc4687144001fafc36c403cfc392725fb79266c.svg)



![{\displaystyle {\begin{aligned}\|Y-{\hat {\mu }}_{m}\|_{{\mathcal {H}}^{T}}^{2}=\sum _{d\in [\![1,D-1]\!]}C_{\tau _{d},\tau _{d+1}},\end{aligned}}}](https://img.franco.wiki/i/9d487d5efc161c2bf77fd72e126763931f82d7f6.svg)
![{\displaystyle ~(\tau ,\tau ^{'})\in [\![1,T]\!]^{2},~\tau <\tau ^{'}}](https://img.franco.wiki/i/7df2d901b5a831ce553fb06ead4fe55b6525c0b7.svg)

![{\displaystyle {\begin{aligned}\|Y-{\hat {\mu }}_{m}\|_{{\mathcal {H}}^{T}}^{2}&=\sum _{d\in [\![1,D-1]\!]}\sum _{i\in [\![\tau _{d},\tau _{d+1}-1]\!]}\|Y_{i}-\left({\hat {\mu }}_{m}\right)_{i}\|_{\mathcal {H}}^{2}\\&=\sum _{d\in [\![1,D-1]\!]}\sum _{i\in [\![\tau _{d},\tau _{d+1}-1]\!]}\left[\|Y_{i}\|_{\mathcal {H}}^{2}+\|{\frac {1}{\tau _{d+1}-\tau _{d}}}\sum _{j=\tau _{d}}^{\tau _{d+1}-1}Y_{j}\|_{\mathcal {H}}^{2}-2<Y_{i},{\frac {1}{\tau _{d+1}-\tau _{d}}}\sum _{j=\tau _{d}}^{\tau _{d+1}-1}Y_{j}>_{\mathcal {H}}\right]\\&=\sum _{d\in [\![1,D-1]\!]}\left(\sum _{i\in [\![\tau _{d},\tau _{d+1}-1]\!]}\|Y_{i}\|_{\mathcal {H}}^{2}-{\frac {1}{\tau _{d+1}-\tau _{d}}}\sum _{i=\tau _{d}}^{\tau _{d+1}-1}\sum _{j=\tau _{d}}^{\tau _{d+1}-1}<Y_{i},Y_{j}>_{\mathcal {H}}\right)\\&=\sum _{d\in [\![1,D-1]\!]}\left(\sum _{i=\tau _{d}}^{\tau _{d+1}-1}k(X_{i},X_{i})-{\frac {1}{\tau _{d+1}-\tau _{d}}}\sum _{i=\tau _{d}}^{\tau _{d+1}-1}\sum _{j=\tau _{d}}^{\tau _{d+1}-1}k(X_{i},X_{j})\right)\\&=\sum _{d\in [\![1,D-1]\!]}C_{\tau _{d},\tau _{d+1}}.\end{aligned}}}](https://img.franco.wiki/i/a4c3ee39d603c59dec2ca4ce7c2c25a4816d13d7.svg)
![{\displaystyle C=(C_{i,j})_{(i,j)\in [\![1,T]\!]}(i<j)}](https://img.franco.wiki/i/968ecda021a68c0af7c0a2b040dc94279f350eb0.svg)
![{\displaystyle \{{\hat {m}}_{D}\}_{D\in [\![1,D_{max}]\!]}}](https://img.franco.wiki/i/459f103b241f13f0e2f1d73c5b9f1f219b04753c.svg)

![{\displaystyle d\in [\![2,D_{max}]\!]}](https://img.franco.wiki/i/7d59c1a388024e8815f605b13dd6a7eb06dc513d.svg)
![{\displaystyle \tau ^{'}\in [\![d,T]\!]}](https://img.franco.wiki/i/c63c9817c704450063627d2e37b7a3df170988ee.svg)




![{\displaystyle {\begin{aligned}{\hat {D}}={\underset {D\in [\![1,D_{max}]\!]}{\operatorname {arg\,min} }}\{\|Y-{\hat {\mu }}_{{\hat {m}}_{D}}\|_{{\mathcal {H}}^{T}}^{2}+pen({\hat {m}}_{D})\},\end{aligned}}}](https://img.franco.wiki/i/3124df24e24d111d1a42caf3259b18d5f95b0e9e.svg)


![{\displaystyle j_{1}\in [\![2,T-1]\!]}](https://img.franco.wiki/i/15af2b7f12af2cb5586ea7fbdc5223878b54d562.svg)





![{\displaystyle j\in [\![2,T-1]\!]}](https://img.franco.wiki/i/4e7cdfca712cad41aceb60021cafb9552372afbb.svg)




![{\displaystyle [\![2,{\hat {\tau }}_{1}-1]\!]}](https://img.franco.wiki/i/34f3e1ae2e5fa3007ee11b12265ce547383e7a7c.svg)
![{\displaystyle [\![{\hat {\tau }}_{1}+1,T-1]\!]}](https://img.franco.wiki/i/b202a6ba98dade00ad10f8af91a0e6d4ff60b636.svg)
![{\displaystyle j_{2}={\underset {j\in [\![2,{\hat {\tau }}_{1}-1]\!]}{\operatorname {arg\,min} }}\|Y_{1}^{{\hat {\tau }}_{1}}-{\hat {\mu }}_{m_{2}}\|_{{\mathcal {H}}^{{\hat {\tau }}_{1}}}^{2},}](https://img.franco.wiki/i/67c225fa326461c798ceaecf84195ce277ed7626.svg)






