Courbe de Wöhler

Divers types de sollicitations sinusoïdales.

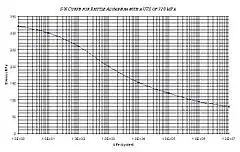
La courbe de Wöhler est le plus ancien diagramme qui permette de visualiser la tenue de la pièce ou des matériaux dans le domaine de fatigue. Cette courbe définit une relation entre la contrainte appliquée σ (sigma parfois notée S) et le nombre de cycles à la rupture NR (en fait nombre de cycles pour lesquels on observe P% de ruptures). En pratique, la courbe de Wöhler est généralement donnée pour une probabilité de rupture P = 0,5.

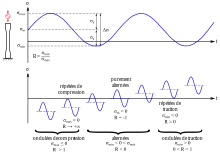
Pour la tracer, on réalise généralement des essais simples qui consistent à soumettre chaque éprouvette à des cycles d’efforts périodiques, d’amplitude de chargement constante S_a fluctuant autour d’une valeur moyenne fixée et à noter le nombre de cycles au bout duquel l’amorçage d’une fissure est observé, appelé ici nombre de cycles à rupture NR ; ceci est fait pour plusieurs valeurs de l'amplitude alternée Sa et de R ; le rapport de charge R est le rapport de la contrainte minimum à la contrainte maximum du cycle périodique. Pour plus de commodité, ce nombre NR est reporté en abscisse sur une échelle logarithmique, et l’amplitude de contrainte Sa est reportée en ordonnée sur une échelle linéaire ou logarithmique pour plusieurs valeurs de R. R=-1 correspond à un cycle symétrique alterné, R=0 correspond à un cycle répété, R>0 correspond à des contraintes ondulés. La décomposition du chargement (par la méthode de comptage rainflow) permet d'exprimer celui-ci en cycles simples caractérisés par une contrainte alternée Sa et un rapport de charge R. Ainsi, à chaque structure essayée, correspond donc un point du plan (NR, Sa) et à partir d’un certain nombre d’essais à contrainte généralement décroissante, on peut établir la courbe de Wöhler.

La caractérisation d'un matériau dans le domaine de la fatigue conventionnelle peut être faite par les courbes de Wöhler, en fonction du rapport de charge R, issues d'essais sur éprouvettes lisses. On peut aussi effectuer des essais sur éprouvettes entaillées pour valider les méthodes de calcul en fatigue des structures.

On définit généralement :

• la fatigue conventionnelle dite « à grand nombre de cycles » au-delà de 50 000 cycles, les courbes de Wöhler obtenues avec des essais de fatigue en effort imposé sont pertinentes.
• la fatigue oligocyclique en deçà de 50 000 cycles, domaine dans lequel il y a interaction entre deux modes de ruine, la fatigue et l'instabilité ductile.

La modélisation des courbes de Wöhler exige donc la représentation des deux modes de ruine couplés.

On remarque que la courbe présente une asymptote horizontale pour N tendant vers +∞. Cela signifie que pour les amplitudes de contrainte σ_a faibles, on ne peut pas avoir de rupture en fatigue dans des délais raisonnables (plusieurs années…).

Certains matériaux, comme les alliages d'aluminium, semblent avoir une asymptote nulle, d'autres une asymptote positive appelée limite d'endurance et notée σ_D ou SaD.

La détermination de la limite d'endurance se fait par des méthodes d'essais tronqués, c'est-à-dire que l'on se positionne à un nombre de cycles donné — typiquement un à cent millions (10⁶ à 10⁸) — et que l'on fait des essais à plusieurs niveaux d'amplitude de contrainte σ_a.

On utilise habituellement trois modèles pour représenter la courbe de Wöhler de manière analytique :

• le modèle de Basquin : il décrit la partie centrale de la courbe, comme une droite dans un diagramme log-log
  N⋅σ_a^m = C
  σ_a = (C/N)^1/m
  log(N) = log(C) - m⋅log(σ_a)
  où C et m sont des paramètres déterminés par régression linéaire dans l'échelle log-log ; 1/m est de l'ordre de 0,1[1] ;
• le modèle de Strohmeyer, qui décrit la partie centrale ainsi que l'asymptote finale,
  N⋅(σ_a - σ_D)^m = C
  ${\displaystyle \mathrm {N} =\left({\frac {\mathrm {A} }{\sigma _{\mathrm {a} }-\sigma _{\mathrm {D} }}}\right)^{m}}$
  avec C = A^m
  ${\displaystyle \sigma _{\mathrm {a} }=\sigma _{\mathrm {D} }+\left({\frac {\mathrm {C} }{\mathrm {N} }}\right)^{1/m}}$ ;
• le modèle de Bastenaire qui décrit également le comportement oligo-cyclique,
  ${\displaystyle \mathrm {N} ={\frac {\mathrm {A} }{\sigma _{\mathrm {a} }-\sigma _{\mathrm {D} }}}\exp \left(-\left({\frac {\sigma _{\mathrm {a} }-\sigma _{\mathrm {D} }}{\mathrm {B} }}\right)^{c}\right)}$.

On remarque que la courbe de Wöhler est une courbe σ_a = ƒ(N), alors que les modèles sont souvent présentés sous la forme N = ƒ(σ_a).

Le fait de disposer d'un modèle mathématique permet de réduire le nombre d'essais nécessaire pour déterminer la courbe. En particulier, pour une classe de matériau donné, on peut avoir un paramètre fixe, typiquement la pente m de la loi de Basquin, ce qui permet de réduire encore le nombre d'essais nécessaire.

• Fatigue
• Essai de fatigue
• Essai de traction
• August Wöhler

• Norman E. Dowlings, Mechanical behavior of materials, Englewood Cliffs (NJ), Prentice Hall, 1993, 780 p. (ISBN 0-13-026956-5)
• J. Lemaitre J.-L. Chaboche, Mécanique des matériaux solides, Paris, Dunod, 1988, 544 p. (ISBN 2-04-018618-2)
• (en) Jean Philibert et al., Métallurgie : du minerai au matériau, Paris, Dunod, 2002, 2^e éd., 1177 p. [détail des éditions] (ISBN 2-10-006313-8), « IV-7, V-11 », p. 913-928, 1104-1110