Couplage scalaire
Le couplage scalaire, noté J et aussi appelé couplage dipôle-dipôle indirect ou juste couplage, est une interaction entre plusieurs spins à travers les liaisons chimiques. C'est une interaction indirecte entre deux spins nucléaires qui provient des interactions hyperfines entre les noyaux et la densité électronique locale[1] et provoque un éclatement du signal RMN. Le couplage scalaire contient des informations sur la distance à travers les liaisons chimiques et les angles entre ces liaisons. Plus important encore, les couplages scalaires permettent d'obtenir des informations importantes sur la connectivité entre les atomes, c'est-à-dire des informations sur la structure de la molécule.
| Couplage harmonique Couplage rotation–vibration Interaction fluide-structure |
| Couplage quantum-mécanique Spectroscopie rotavibrationnelle Couplage vibronique Couplage de moment cinétique Couplage scalaire |
Origine
Pour l'origine du couplage scalaire, voir Les interactions dipolaires magnétiques.
Constante de couplage
La constante de couplage est la valeur moyenne (en solution) de l'intensité de l'interaction dipolaire à l'origine du couplage. Elle est notée nJij et exprimée en Hz ; n représente le nombre de liaisons reliant les spins i et j. Cette valeur correspond également à la différence entre les niveaux d'énergie générés par le couplage.
Ordre du couplage
Lorsque la différence de déplacement chimique en hertz (Δν) est supérieure à 5-10 fois la constante de couplage J (en valeur absolue), le couplage est dit du premier ordre. En dessous de cette limite, le couplage est dit du second ordre et cela peut compliquer notablement l'interprétation car l'intensité des différents pics est très altérée (voir ci-dessous Systèmes de spins et Répartition des spins).
Valeurs représentatives
| Noyau 1 | Noyau 2 | Valeurs représentatives |
|---|---|---|
| 1H | 1H | 2JH-H ≈ -13 Hz 3JH-H ≈ 7 Hz (aliphatique) 3JH-H ≈ 8 Hz (aromatique) |
| 1H | 13C | 1JC-H ≈ 120-300 Hz |
| 1H | 31P | 1JP-H ≈ 550-800 Hz |
Systèmes de spins
Lorsque l'on étudie des spins couplés entre eux, on parle d'un système de spins car ils ne peuvent pas être considérés indépendamment les uns des autres. Notez que ces spins peuvent correspondre à des noyaux différents.
Dans des cas relativement simples, on utilise généralement les règles suivantes :
- Les spins sont notés individuellement par une lettre majuscule donc la position dans l'alphabet correspond très approximativement à leur déplacement chimique : A, B, C..., M, N, O... et X, Y, Z. Si un des spins correspond à un hétéroatome, il est automatiquement placé dans le groupe A, B, C... ou X, Y, Z.
- Le nombre de spins magnétiquement équivalents est indiqué en indice, par exemple A2X ou A2B2.
- Les spins connectés au même atome mais magnétiquement non-équivalents sont différenciés par des apostrophes, par exemple AA'BB' pour un groupe –CH2CH2– (si la règle de non-équivalence est respectée).
- Les spins magnétiquement équivalents (par symétrie) mais non-liés au même atome sont également différenciés par des apostrophes.
Multiplicité
Le cas général est qu'un spin couplé à un noyau de spin s produit 2s+1 niveaux d'énergie ce qui se traduit, sur le spectre RMN, par un éclatement du signal : au lieu de produire un pic unique, on observe 2s+1 pics de même intensité séparés par J, la constante de couplage. Si ce spin est couplé à d'autres spins, tous les pics sont à nouveau éclatés, ce que l'on appelle un multiplet. Notez que la surface totale, peu importe les éclatements du pic, reste constante et proportionnelle au nombre de spins magnétiquement équivalents. Ci-dessous, le couplage entre 1 spin 1/2 et : 1 spin 1/2 (à gauche, doublet, système AX), 2 spins 1/2 (au milieu, triplet système AX2) et 3 spins 1/2 (à droite, quadruplet système AX3). Dans tous les cas, la même constante de couplage J a été utilisée et cause la superposition de certains pics, ce qui explique la différence d'intensité relative des pics : 1:1 pour un doublet, 1:2:1 pour un triplet et 1:3:3:1 pour un quadruplet.
| Multiplicité | Rapport d'intensités |
|---|---|
| Singulet (s) | 1 |
| Doublet (d) | 1:1 |
| Triplet (t) | 1:2:1 |
| Quadruplet (q) | 1:3:3:1 |
| Quintuplet | 1:4:6:4:1 |
| Sextuplet | 1:5:10:10:5:1 |
| Septuplet | 1:6:15:20:15:6:1 |
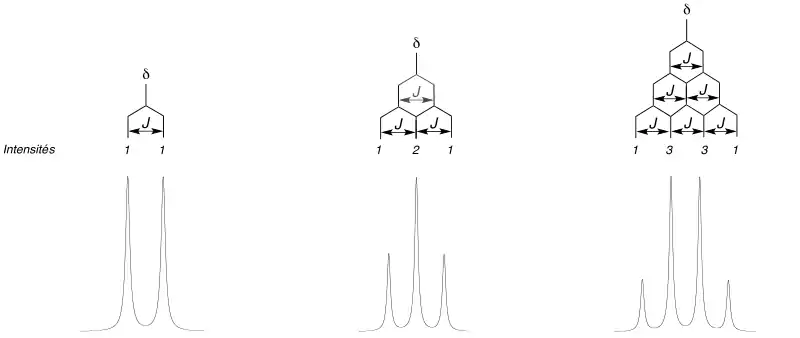
Si l'on se cantonne à des spins 1/2, l'intensité relative des pics d'un multiplet suit donc le triangle de Pascal (ci-contre).
On peut traiter de la même façon un système de spins AMX2 dans lequel un spin A est couplé à un spin M (avec une constante de couplage JAM) et à deux spins X magnétiquement équivalents (avec une constante de couplage JAX. Ci-dessous, la simulation d'un système AMX2 avec JAX = 7 Hz et JAM = 2 Hz. On obtient ce que l'on nomme un doublet de triplet (abrév. dt) ou un triplet dédoublé.
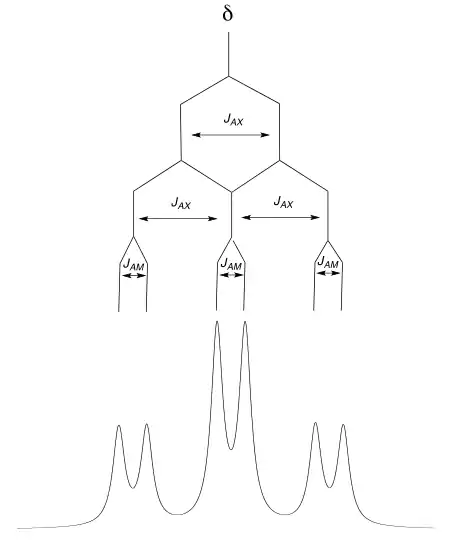
Répartition des spins
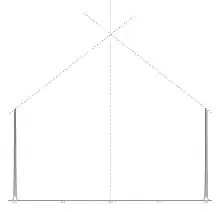
Lorsque plusieurs spins sont couplés, la répartition des spins sur les différents niveaux d'énergie est modifiée de sorte que la population des niveaux les plus extrêmes est appauvrie. Pour des systèmes de spins assez simples, cela se traduit par ce que l'on appelle l'effet de toit. Dans le cas idéal, on peut tracer deux droites suivant l'intensité des pics des multiplets qui se croisent à la moyenne des déplacements chimiques.
Dans les cas plus complexes qui font intervenir des couplages de second ordre, il est nécessaire de faire appel à la simulation des systèmes de spins et comparer la simulation avec le résultat expérimental.
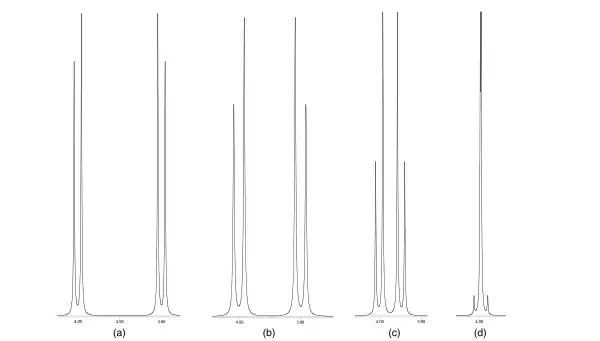
Dans la figure ci-dessous, un système de 2 spins a été simulé à 400 MHz et avec une constante de couplage de 7 Hz : (a) δ = 4,00 et 3,80 ppm ; (b) 4,00 et 3,90 ppm ; (c) 4,00 et 3,95 ppm ; (d) 4,00 et 3,99 ppm. On est encore dans le cadre du couplage du premier ordre dans le cas (a) mais le cas (b) est déjà un cas limite avec Δν ≃ 6J. Les cas (c) et (d) sont vraiment des couplages du second ordre avec une énorme modification de l'apparence des doublets. Si les déplacements chimiques sont identiques, on n'observe qu'un singulet.
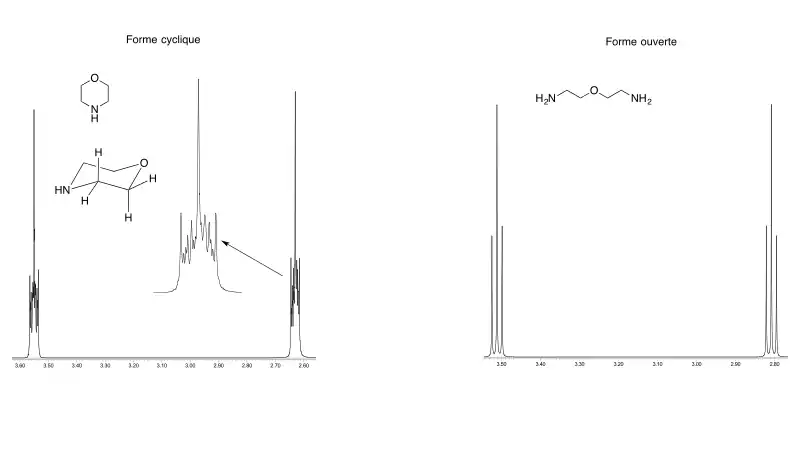
Système AA'XX' vs A2X2
Dans l'exemple ci-dessous, sont comparés le spectre 1H-RMN de la morpholine (à gauche) et de sa forme ouverte (à droite). Dans le cas de la forme ouverte, la rotation libre des liaisons permet de moyenner les déplacements chimiques et les constantes de couplage. Il en résulte un spectre très simple où les deux groupes CH2 sont couplés entre eux et forment deux triplets. Il s'agit d'un système A2X2 dans lequel on observe un léger effet de toit.
Au contraire, la morpholine (à gauche du schéma) est cyclique. Même si le cycle peut changer de conformation, cela ne suffit pas pour moyenner les constantes de couplage. Il en résulte un système AA'XX' dans lequel chaque noyau est couplé à 3 autres noyaux et avec des constantes de couplage différentes. Il en résulte deux multiplets quasiment identiques mais extrêmement complexes dont la forme est assez caractéristique (un singulet au centre, un multiplet très complexe avec deux singulets un peu plus intenses sur les bords avant une chute brutale du signal).
Découplage
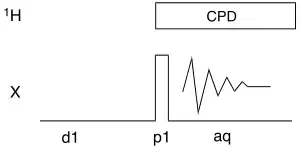
Si le couplage apporte de nombreuses informations, il est aussi une source de confusion lorsque de nombreux signaux couplés ont des déplacements chimiques proches. Dans ce cas on obtient ce que l'on surnomme une forêt de pics que l'on ne peut interpréter. On souhaiterait alors que le noyau que l'on observe ne soit plus couplé à un ou plusieurs autres noyaux. Il est assez rare que l'on dispose d'une sonde et de l'électronique permettant de découpler un noyau de plusieurs autres noyaux. Néanmoins il est aisé de découpler un noyau d'un (seul) autre. C'est d'ailleurs ce que l'on fait quasi-systématiquement pour une RMN du carbone-13 pour le découpler du proton. Ceci est noté "13C {1H}".
Les spectromètres assez anciens permettent de faire un découplage en "onde continue" (cw ou Continuous wave en anglais) : dans ce cas de figure, le noyau à découpler est irradié en permanence par des radiofréquences de faible intensité, ce qui moyenne le couplage à 0 Hz. Sur les spectromètres plus récents, il n'est plus possible d'effectuer une irradiation continue. On utilise alors différents programmes d'irradiation dite "composite" pour obtenir le même résultat : la sonde envoie une séquence rapprochée d'impulsions sur une certaine gamme spectrale du noyau à découpler. On note ceci CPD, de l'anglais Composite Pulse Decoupling. Les programmes de découplage les plus connus sont MLEV (Malcolm Levitt), GARP (Globally optimized Alternating-phase Rectangular Pulses), WALTZ ou DIPSI (Decoupling In the Presence of Scalar Interactions), chaque méthode ayant des limitations différentes. Ces programmes de base sont écrits sous la forme PRG-n où n décrit les variantes de la séquence, en général le nombre de cycles de façon directe ou indirecte : GARP-1, WALTZ-16, DIPSI-3, etc.
Comparaison des programmes de découplage[2] :
- MLEV : le plus ancien dans cette liste, MLEV provoque un élargissement important des pics et requiert beaucoup d'énergie, ce qui peut provoquer un échauffement de l'échantillon. Il n'est plus utilisé à l'heure actuelle.
- GARP : il provoque un élargissement modéré des pics et l'intensité du découplage n'est pas tout à fait homogène. En revanche, il permet un découplage sur une gamme spectrale beaucoup plus large (2-3 fois celle de WALTZ).
- WALTZ : il offre une bonne gamme spectrale pour le découplage, mais 2-3 fois inférieure à GARP. Cependant, l'homogénéité et la puissance du découplage sont bien meilleurs et l'élargissement des pics est faible.
- DIPSI : ce programme a été spécialement conçu pour découpler des noyaux qui sont très couplés par ailleurs, contrairement aux programmes précédents. En plus de cette spécificité importante, cette séquence permet d'obtenir un élargissement des pics faible (DIPSI-1 et 2), voire très faible (DIPSI-3). Le principal inconvénient est que la gamme spectrale est inférieure à celle de WALTZ ; même DIPSI-3 (la plus longue séquence) a une gamme spectrale inférieure à WALTZ-16.
Attention : sauf exceptions, si l'on utilise un découplage, il n'est plus possible d'intégrer les signaux RMN de façon fiable sur le spectre. Ceci est dû à l'apparition de l'effet Overhauser nucléaire lors du découplage. Cependant, certaines séquences d'impulsion permettent de minimiser l'effet Overhauser afin de pouvoir effectuer une intégration fiable sur les pics RMN, comme la séquence zgig (zg Inverse-Gated) ; voir Découplage sans effet Overhauser ci-dessous.
Découplage standard
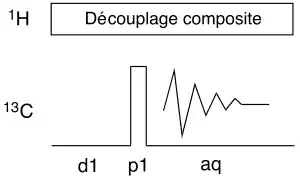
La séquence d'impulsions la plus simple utilisée pour les spectres 13C découplés du proton est représentée ci-dessous. Le découplage composite est appliqué en permanence tout au long de l'expérience, ce qui implique que l'effet Overhauser nucléaire sera rapidement maximum. On utilise également cette séquence pour bon nombre d'autres noyaux si l'on n'a pas besoin d'intégrer les pics du spectre.
Découplage sans effet Overhauser
L'effet Overhauser nucléaire est parfois gênant car il modifie l'intensité des pics découplés. Pour les noyaux ayant des rapports gyromagnétiques γ de signes opposés, l'effet Overhauser peut mener à la suppression d'un voire tous les signaux. Dans cette expérience, nommée Inverse-Gated decoupling en anglais, on profite du fait que le découplage a un effet instantané alors que l'effet Overhauser met un certain temps à apparaître. Si l'on n'effectue un découplage que pendant l'acquisition en conservant un temps d'acquisition (AQ) faible, et un délai d1 au moins égal à 10 fois AQ, on peut détecter le signal X découplé sans effet Overhauser. Afin de réduire le temps de relaxation, on peut être amené à ajouter à l'échantillon un agent de relaxation comme Cr(acac)3 à une concentration de 0,1 M.
Au-delà du couplage - RMN de corrélation
Le couplage est intéressant dans les spectres simples car il permet d'étudier la connectivité des différents noyaux. Cependant il est plutôt envahissant dans l'étude de molécules complexes.
Ce qu'il faut retenir de cela est que les spins sont couplés à tous les spins environnant et que l'on peut détecter tous ces couplages, même s'ils n'apparaissent pas forcément sur les spectres 1D. Ces spins échangent une certaine quantité d'énergie et l'on dit dans ce cas que tous ces spins sont "corrélés". Cela a ouvert la voie à la RMN de corrélation. S'il est vrai que la RMN de corrélation a surtout été rendue célèbre à travers la RMN-2D (basse résolution), il est tout à fait possible d'utiliser la RMN de corrélation en 1D et en haute résolution.
Voir aussi
Références
- E. L. Hahn and D. E. Maxwell, « Spin Echo Measurements of Nuclear Spin Coupling in Molecules », Phys. Rev., vol. 88, no 5, , p. 1070–1084 (DOI 10.1103/PhysRev.88.1070, Bibcode 1952PhRv...88.1070H)
- Rule, G.S., Hitchens, T.K.; Fundamentals of Protein NMR Spectroscopy, Springer, 2006, pp. 530