Contraction d'arête
En théorie des graphes, une contraction d'arête est une opération sur un graphe. Elle consiste, de façon imagée, à contracter une arête d'un graphe, ce qui revient à fusionner ses deux extrémités.
Cette opération est fondamentale pour la théorie des mineurs de graphe et elle est utilisée dans certains algorithmes et certaines preuves.
Définition
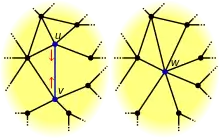
Soit un graphe G=(V,E), contenant une arête (u,v), avec u différent de v. La contraction de (u,v) est l'opération qui consiste à transformer G en un graphe G'=(V',E'), où V' est égal à V mise à part que u et v sont remplacés par un unique sommet w, et E' est égal à E mis à part que les occurrences de u et v sont remplacés par w.
Selon le domaine d'application, on enlève ou non les boucles et les multi-arêtes créées par la contraction.
Utilisations
L'algorithme de Karger pour la coupe min[1] - [2], et l'algorithme de Borůvka pour l'arbre couvrant de poids minimum[3] - [4] utilisent la contraction d'arêtes.

Notes et références
- David Karger, « Global Min-cuts in RNC and Other Ramifications of a Simple Mincut Algorithm », dans Proc. 4th Annual ACM-SIAM Symposium on Discrete Algorithms, (lire en ligne)
- Notes du cours de Sanjeev Arora (Université de Princeton).
- (cs) Otakar Borůvka, « O jistém problému minimálním (About a certain minimal problem) », Práce mor. přírodověd. spol. v Brně III, vol. 3, , p. 37–58.
- « Algorithme de Boruvka », sur COATI chez INRIA.