Construction d'un cercle point par point
La construction d'un cercle point par point est un exercice de géométrie visant à construire un cercle ou un arc de cercle d'une autre manière qu'avec un compas. Il existe plusieurs méthodes pour construire un cercle point par point. Ces méthodes peuvent paraître plus ou moins complexe mais elles sont explicités ci-dessous. Des logiciels spécifiques doivent être parfois appliqués pour certaines méthodes.
Premier exemple
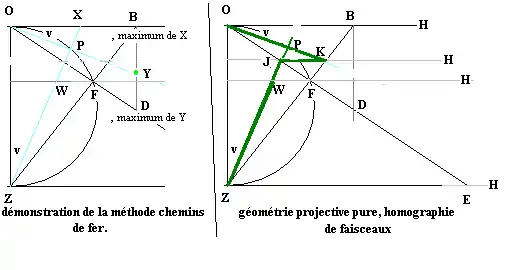
Méthode des chemins de fer
En introduction à la construction homographique d'un cercle, la méthode des chemins de fer peut être citée. On veut, à partir d'un point O d'une ligne droite, prendre un virage à droite sur un angle de 45° avec un rayon R = 300m, on n'a pas accès au centre du cercle. Il faut pourtant tracer l'arc de cercle point par point en plantant des piquets avec une précision suffisante.

La méthode consiste à créer trois « échelles » X, Y, W graduées en n subdivisions égales, 16 par exemple, à relier les points correspondants des échelles X et W, à relier l'origine au point correspondant de l'échelle Y, le point d'intersection de ces deux droites est un point P du cercle. Si les 16 points ne suffisent pas on peut encore subdiviser les trois échelles en 32 parties, ou 64. Les échelles sont positionnées selon des calculs trigonométriques élémentaires. Le maximum (B) de l'échelle X est 2R tan(α/2), 248,53m dans notre exemple, le maximum de l'échelle Y est 2R tan2(α/2), le maximum de l'échelle W est R sin(α) et le positionnement de cette échelle est à l'ordonnée R(1-cos(α)).
Explication de cette méthode
La propriété du cercle utilisée ici est l'angle droit défini par un diamètre OZ. L'échelle W est positionnée judicieusement pour être homothétique de centre Z à l'échelle X, le rapport d'homothétie étant cos2(α/2). La droite (WX) passe donc par Z, point qui à l’origine du problème est encore plus inaccessible que le centre du cercle. L'échelle Y est positionnée de façon que les triangles BOZ et DBO soient semblables. Ce qui implique que lorsque l'on fait correspondre une position X à une position Y, les triangles XOZ et YBO sont semblables, les angles OBY et OZX=v sont égaux, donc les droites OY et ZX sont perpendiculaires.
Leur intersection P est sur le cercle de diamètre OZ.
Fonction homographique mise en jeu
On raisonne à partir de l'angle θ= OZX=OBY. La position de X sur son échelle est 2Rtan(θ). La position de Y sur son échelle est 2Rtan(α/2)tan(θ), la relation entre X et Y est
- qui n'est qu'un cas particulier et dégénéré de la fonction homographique
- dans laquelle c=0, d=1, b=0, a=tan(α/2).
Ceci illustre de manière analytique la propriété générale selon laquelle une conique est engendrée par l'intersection de deux faisceaux de droites en correspondance homographique, ici les faisceaux de centre Z et O.
Explication par la géométrie projective pure
Dans le plan de cette figure considéré comme plongé dans un plan projectif fondamental, on peut établir une (parmi d'autres possibles) transformation homographique entre les deux êtres mathématiques unidimensionnels que sont les faisceaux de centre Z et O. Ceci en se dispensant de travailler sur les échelles de points X et Y. On utilisera H, le point à l'infini dans la direction de l'axe OX et le faisceau de droites de centre H, c’est-à-dire le faisceau des droites parallèles à OX.
- Soit la transformation T définie comme la succession de 2 transformations projectives unidimensionnelles; la première est la transformation du faisceau Z en faisceau H en s'appuyant sur la droite (OE); la deuxième est la transformation du faisceau H en faisceau O en s'appuyant sur la droite (ZB); sur la base de 3 points connus du cercle (O, F et Z), examinons les transformations de trois droites du faisceau de départ.
- la droite ZO devient HO qui est égale à HB qui devient ensuite OB, l'intersection de ZO et OB étant O, point du cercle.
- la droite ZB qui est égale à ZF devient HF qui devient ensuite OF, l'intersection de ZB et OF étant F, point du cercle.
- la droite ZE devient HE qui est égale à HZ qui devient ensuite OZ, l'intersection de ZE et OZ étant Z, point du cercle.
- Le théorème fondamental de la géométrie projective nous assure que T est définie de manière unique par ces trois points Z, H, O et ces deux droites d'appui (OE) et (ZB). Si nous observons maintenant un droite variable du faisceau, ZX
- la droite ZX qui est égale à ZJ devient HJ qui est égale à HK qui devient ensuite OK, l'intersection de ZX et OK étant P, point variable de la conique.
Or dans le triangle OKZ, on a deux hauteurs OF et KH qui se coupent en J qui est donc l'orthocentre. Ce qui implique que l'angle en P est droit, donc que P est sur le cercle. On vérifie ainsi que la conique définie par la transformation projective unidimensionnelle T est bien le cercle considéré.
Articulation entre la géométrie projective et la géométrie euclidienne
Cet exemple en géométrie projective se résume à tracer des points P d'une conique passant par les 3 points O,Z,F et possédant 2 tangentes OB et ZE. Elle se construit par les faisceaux de centre Z et O liés par l'homographie T. Au stade de la géométrie projective, tout ce qu'on peut affirmer c'est que l'ensemble des points P est une conique.
- Pour parler d'un cercle, nous avons besoin de notion métrique. Ici la notion pertinente est l'orthogonalité : les tangentes OB et ZE sont perpendiculaires à la corde ZO, l'angle F est droit, les droites du faisceau H sont toutes perpendiculaires à OZ.
Deuxième exemple
Un arc de cercle, méthode projective
Dans cet exemple l'arc de cercle n'est pas nécessairement un demi-cercle. Par exemple un arc de cercle GD, avec le point S au milieu de l'arc de cercle, et les deux tangentes symétriques GH et DH. Pour trouver un point variable P de la conique on travaille sur les faisceaux de centres D, H, G en s'appuyant sur les droites (SJ) et (SK).
- La droite de départ est DW qui coupe SK en B
- la droite intermédiaire est HB qui coupe SJ en C
- la droite d'arrivée est GC qui coupe la droite de départ DW en P, point à construire.
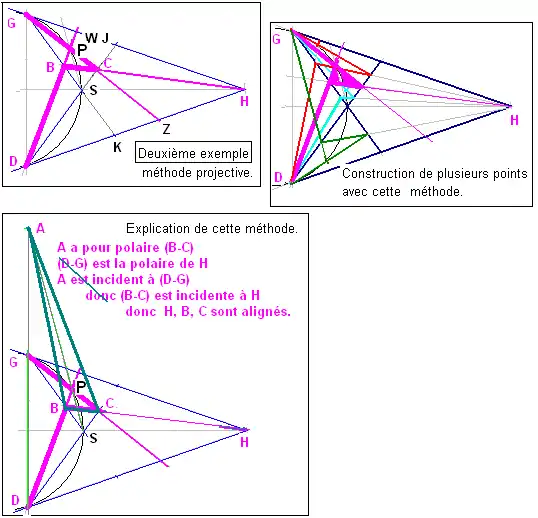
Explication de cette méthode
L'idée de base est de travailler avec les polaires par rapport à la conique.
- la corde joignant deux points de la conique est la polaire de l'intersection des deux tangentes en ces points, donc GD polaire de H.
- quatre points sur une conique forment un quadrangle dont le triangle diagonal est autopolaire, donc à partir du quadrangle GDSP le triangle ABC est autopolaire, donc BC est la polaire de A.
- le théorème de la réciprocité polaire implique que si A est sur GD, alors H est sur BC.
Variantes possibles des faisceaux homographiques
La figure du triangle autopolaire ABC peut être complétée par des propriétés projectives issues du théorème de Désargues et de propriétés harmoniques.
- BC est aussi la polaire de A par rapport à la bidroite { HG ; HD}.
- B étant sur cette polaire, alors WK passe aussi par A.
- C étant sur cette polaire, alors JZ passe aussi par A.
Soit Y l’intersection de WZ et JK. Si on considère le quadrangle WKZJ de cette bidroite, le triangle AYH est autopolaire par rapport à cette bidroite, donc Y est situé sur la droite HBC.

La première variante de quatre faisceaux homographiques est la suivante :
- La droite de départ est DW du faisceau D, elle coupe la droite d’appui GH en W ;
- La deuxième droite, du faisceau K est KW, elle coupe la droite d’appui DG en A ;
- La troisième droite, du faisceau J est AJ, elle coupe la droite d’appui DH en Z ;
- La droite d’arrivée, du faisceau G, est ZG, elle coupe la droite de départ en P, point de notre conique.
La deuxième variante est moins orthodoxe en ce sens qu’elle met en jeu trois faisceaux de droites (centrés sur D, H, G) mais aussi un quatrième ensemble de droites (les droites WY) qui ne passent pas par un point commun (mais qui en réalité enveloppent une autre conique).
- La droite de départ est DW du faisceau D, elle coupe la droite d’appui GK en B et la droite d’appui GH en W ;
- La deuxième droite, du faisceau H est BH, elle coupe la droite d’appui JK en Y.
- La troisième droite WJ qui n’appartient à aucun faisceau, coupe la droite d’appui DH en Z ;
- La droite d’arrivée, du faisceau G, est ZG, elle coupe la droite de départ en P, point de notre conique.
Cette variante est mentionnée à titre d’ouverture sur d’autres propriétés projectives des coniques, elle n’est pas économique en termes de construction point par point.
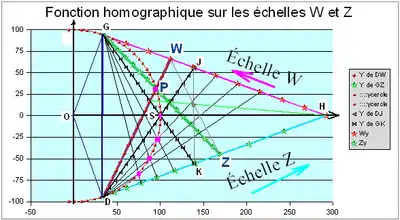
Fonction homographique mise en jeu
On travaille avec les deux échelles W et Z situées sur les deux tangentes issues du point H, orientées de H vers G ou D.
Il y a deux constantes, l la longueur HG=HD, k la longueur HK=HJ.
Le dessin sur tableur a été effectué avec R=100 et l'angle de l'arc choisi pour que tan(a/4)=0,7 ; sur l'échelle W on a effectué une subdivision uniforme en 10 parties, ce qui donne sur l'échelle Z des subdivisions non uniformes car la fonction homographique n'est pas dégénérée.
- Cette fonction homographique mise en jeu est
- qui s'écrit aussi
- , elle correspond bien aux trois couples de cordes suivants :
- w=0; z=l; points W en G et Z en H; cordes DG et GH qui se coupent en G.
- w=l; z=0; points W en H et Z en D; cordes DH et GD qui se coupent en D.
- w=k; z=k; points W en J et Z en K; cordes DJ et GK qui se coupent en S.
On remarque que cette formule homographique ne contient que(wz) et (w+z), elle est symétrique en w et z, ce qui découle de la symétrie complète de la figure selon la droite SH. Dans ce cas on dit que la fonction homographique est involutive, c’est-à-dire égale à sa réciproque. On peut aussi l'exprimer avec les données de la figure, le rayon du cercle R et l'angle de l'arc a. Il faut effectuer quelques calculs trigonométriques; ils seront facilités par des propriétés de bissectrices : DOG=a, DOH=a/2, HDJ=JDG=a/4, on travaille sur le quart de l'angle, on pose t=tan(a/4); alors <math>k=R 2 t \frac{1+t^2}{(1-t^2)(3-t^2)}, l=\frac{2Rt}{1-t^2}</math> et la fonction homographique devient
qui s'écrira aussi avec la somme et le produit
Articulation entre la géométrie projective et la géométrie euclidienne
Ici la géométrie projective garantit que B, C et H sont alignés sur la polaire de A. La conique est définie par les points G, S et D et les tangentes GH et DH, soit 5 éléments. La transformation homographique T qui transforme la droite (WBD) en (BCH) puis (CGZ) nous garantit que l'intersection P appartient à la conique. La figure est suffisamment riche pour que l'on puisse trouver 2 variantes de compositions de transformations qui aboutissent à T.
- La géométrie euclidienne nous permet d'exploiter des propriétés angulaires du cercle : la figure est symétrique par rapport à OH, l'angle GPD est constant, et il y a quelques propriétés d'angles moités et quart de a. Dans ces conditions on peut calculer précisément la fonction homographique involutive f(w)=z, mais on n'apprend rien de plus qu'avec les nombreux alignements fournis par la géométrie projective.
Bibliographie
- Formulaire technique de mécanique générale, par Jacques Muller (diverses éditions)




![{\displaystyle z=R\left[2t{\frac {1+t^{2}}{1-t^{2}}}\right]\left[{\frac {(1-t^{2})w-2Rt}{(1-t^{2})(3-t^{2})(3t^{2}-1)w-2RT(1+t^{2})^{2}}}\right]}](https://img.franco.wiki/i/c54e23ae8a7fa44b70e91e62c6884a2c1f8d590f.svg)
