Configuration de Möbius

En géométrie, une configuration de Möbius (ou parfois un couple de tétraèdres de Möbius) est une configuration de l'espace euclidien ou de l'espace projectif, formée de deux tétraèdres mutuellement inscrits, c'est-à-dire que chaque sommet de l'un appartient à l'une des faces de l'autre. Autrement dit, il s'agit d'un système de huit points et huit plans, chaque point appartenant à quatre plans et chaque plan contenant quatre points.

Exemple de configuration de Möbius : les plans des faces du tétraèdre rouge sont représentées en haut ; ceux du tétraèdre bleu en bas. Les sommets du tétraèdre rouge ont pour coordonnées

(0,0,0),

(0,0,1),

(0,1,0)

(1,0,0)

; ceux du tétraèdre bleu out pour coordonnées

(0,-\gamma ,\gamma ),

(\gamma ,0,-\gamma ),

(-\gamma ,\gamma ,0)

(\lambda ,\lambda ,\lambda ),

où

\gamma ={\frac {1}{\sqrt {2}}}

\lambda ={\frac {1}{3}}

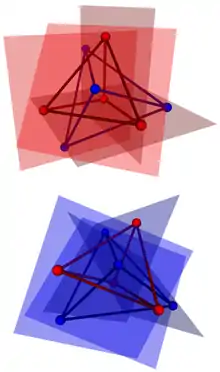
Théorème de Möbius

Ces configurations sont nommées d'après August Ferdinand Möbius, qui a démontré en 1828 que si deux tétraèdres ont sept de leurs sommets dans les plans correspondants des faces de l'autre tétraèdre, il en est de même du huitième sommet. Ce résultat est vrai plus généralement dans tout espace projectif (de dimension 3) si et seulement si le théorème de Pappus y est vrai[1], et est vrai dans un espace construit sur un corps si et seulement si ce corps est commutatif[2]. Par dualité projective, le théorème équivaut à ce que si sept des huit faces de deux tétraèdres contiennent le sommet correspondant de l'autre tétraèdre, il en est de même de la huitième face.

Construction

Coxeter a décrit une construction simple d'une configuration de Möbius[3] : partant d'un point p arbitraire de l'espace, soit A, B, C et D quatre plans passant par p (trois quelconques d'entre eux n'ayant pas de droite en commun) ; on place six points q, r, s, t, u et v sur les six droites d'intersection de ces plans deux à deux, de telle sorte que quatre d'entre eux ne sont jamais coplanaires. Pour chacun des plans A, B, C et D, quatre des sept points p, q, r, s, t, u et v sont dans ce plan ; on note A’, B’, C’ et D’ les plans passant par les trois points restant. Par dualité du théorème, ces quatre nouveaux plans ont en commun le point w ; les huit points p, q, r, s, t, u, v et w et les huit plans A, B, C, D, A’, B’, C’ et D’ forment une configuration de Möbius.

Constructions analogues

Des constructions de configurations combinatoires analogues ont été obtenues à la fin du 19^e siècle par divers auteurs[4] - [5] - [6], arrivant à cinq configurations non dégénérées réalisables dans l'espace euclidien.

Le graphe de Levi de la configuration de Möbius a 16 sommets (correspondant aux huit points et aux huit plans), avec une arête pour chaque relation d'incidence. Il est isomorphe au graphe de l'hypercube Q₄. Une configuration proche, la configuration de Möbius-Kantor (en), formée de deux quadrilatères du plan projectif complexe mutuellement inscrits, a pour graphe de Levi le graphe de Möbius–Kantor, qui est un sous-graphe de Q₄.

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Möbius configuration » (voir la liste des auteurs).

- (de) K. Reidemeister, « Zur Axiomatik der 3-dimensionalen projektive Geometrie », Jahresbericht der Deutschen Mathematiker-Vereinigung, vol. 38,‎ 1929, p. 71 (lire en ligne).
(en) M. W. Al-Dhahir, « A class of configurations and the commutativity of multiplication », The Mathematical Gazette, The Mathematical Association, vol. 40, n^o 334,‎ 1956, p. 241–245 (DOI 10.2307/3609605, JSTOR 3609605).
(en) H. S. M. Coxeter, « Self-dual configurations and regular graphs », Bulletin of the American Mathematical Society, vol. 56, n^o 5,‎ 1950, p. 413–455 (DOI 10.1090/S0002-9904-1950-09407-5, MR 0038078).
(de) P. Muth, « Ueber Tetraederpaare », Zeitschrift für Mathematik und Physik, vol. 37,‎ 1892, p. 117–122 (lire en ligne)
(de) Gustav Bauer, « Von zwei Tetraëdern, welche einander zugleich eingeschrieben und umschrieben sind », Sitzungsberichte der Königlich Bayerischen Akademie der Wissenschaften, Mathematisch-Physikalischen Classe, vol. 27, n^o 2,‎ 1897, p. 359–366 (lire en ligne).
(it) V. Martinetti, « Le configurazioni (8₄,8₄) di punti e piani », Giornale di Matematiche di Battaglini, vol. 35,‎ 1897, p. 81–100 (lire en ligne).

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.