Complétion de Knuth-Bendix
La procédure de complétion de Knuth-Bendix ou complétion de Knuth-Bendix (aussi appelée algorithme de Knuth-Bendix[1] - [2] - [3]) transforme, si elle réussit, un ensemble fini d'identités[4] (sur des termes) décrivant une structure algébrique en un système de réécriture de termes confluent et qui termine (dit alors convergent). Le processus de complétion a été inventé par Donald Knuth[1]aidé d'un étudiant, nommé Peter Bendix, pour la mise en œuvre.

En cas de réussite, la complétion donne un moyen effectif de résoudre le problème du mot pour l'algèbre en question, comme cela a été démontré par Gérard Huet[3] - [5]. Par exemple, pour la théorie équationnelle des groupes (voir schéma à droite), la complétion fournit un système de réécriture de terme confluent et qui termine. On peut alors décider si une équation t1 = t2 est vraie dans tous les groupes (même si décider si une formule du premier ordre est vraie dans tous les groupes est indécidable[6]).
Malheureusement, le problème du mot étant indécidable en général, la procédure de complétion ne se termine pas toujours avec succès. Elle peut soit s'exécuter indéfiniment, soit échouer en rencontrant une identité non-orientable (qu'elle ne peut pas transformer en règle de réécriture sans être sûre de ne pas mettre en danger la terminaison).
Il existe une variante de la procédure de complétion qui n'échoue pas sur les identités non orientables[5]. Elle fournit une procédure de semi-décision pour le problème du mot, autrement dit, elle permet de dire si une identité donnée est déductible des identités qui décrivent l'algèbre en question, dans tous les cas où elle l'est effectivement, mais peut ne jamais terminer.
Ordre de réduction
Pour garantir la terminaison des systèmes de réécriture qui interviennent au cours du processus, mais aussi pour garantir la correction de la méthode, la complétion de Knuth-Bendix prend en entrée un ordre < sur les termes. La relation doit être irréflexive, transitive et bien fondée, close par contexte (si a < b alors x[a]p < x[b]p où x[a]p et x[b]p sont les termes x où on a remplacé le sous-terme en position p par respectivement a et b), close par instanciation (si a < b, alors a[σ] < b[σ] pour toute substitution σ). Une relation qui satisfait ces propriétés est un ordre de réduction.
Exemple : ordre lexicographique sur les chemins
L'ordre lexicographique sur les chemins[7] - [8] est un exemple d'ordre de réduction. C'est un ordre pratique car il est uniquement donné à partir d'un ordre sur les symboles de fonctions. Étant donné un ordre sur les symboles de fonctions il est défini par :
- s > x si x est une variable qui apparaît dans s et s ≠ x
- f(s1, ... sk) > g(t1, ... , tn) si
- ou bien il existe i où si > g(t1, ... , tn)
- ou bien f > g et f(s1, ... sk) > tj pour tout j
- ou bien f = g et f(s1, ... sk) > tj pour tout j et il existe i tq s1 = t1, ..., si-1 = ti-1 et si > ti.
Idée générale
Certains ouvrages[9] présentent d'abord la procédure de complétion sous la forme d'une procédure naïve qui est loin d'une implémentation en pratique mais qui permet de comprendre l'idée générale. La procédure de complétion de Knuth-Bendix prend en entrée un ensemble fini d'identités et un ordre de réduction < sur les termes[10]. En sortie, il produit un système de réécriture pour les identités qui est à la fois confluent, qui termine et qui est compatible avec l'ordre. La procédure peut aussi explicitement dire qu'elle ne parvient pas à construire un tel système de réécriture ou alors elle peut diverger.
Initialisation
La procédure part d'un système de réécriture obtenu en orientant les identités à l'aide de l'ordre < (s'il existe une règle qui n'est pas orientable avec l'ordre <, alors l'algorithme dit qu'il n'existe pas de tel système de réécriture). Par exemple, si l'entrée du problème est :
- 1 * x = x (1 est un élément neutre à gauche)
- x-1 * x = 1 (x-1 est un inverse à gauche de x)
- (x * y) * z = x * (y * z) (* est associative)
et l'ordre lexicographique sur les chemins comme ordre de réduction > où -1 > * > 1, l'algorithme commence avec le système de réécriture suivant :
1 * x → x
x-1 * x → 1
(x * y) * z → x * (y * z)
Boucle de complétion
Ensuite, la procédure complète le système de réécriture en ajoutant des règles supplémentaires afin d'essayer de rendre le système confluent. La complétion s'appuie sur l'ordre < afin de garantir que le système termine toujours.
Durant la complétion, on considère les paires critiques. Pour chaque paire critique (s, t), on calcule des formes normales s' et t' on ajoute s' → t' ou t' → s' en s'aidant de l'ordre <. Par exemple, 1 * z et x-1 * (x * z) forment une paire critique non joignable et sont déjà des formes normales. Comme x-1 * (x * z) > 1 * z, la procédure de complétion ajoute la règle :
x-1 * (x * z) → 1 * z
Ainsi, la complétion ajoute de nouvelles règles au système de réécriture et donc de nouvelles paires critiques apparaissent. Il faut donc continuer à compléter le système de réécriture. La procédure s'arrête avec succès s'il n'y a plus de nouvelles paires critiques non joignables. La procédure s'arrête avec échec s'il y a une paire critique que l'on ne peut pas rendre joignable avec l'ordre <.
Entrée : un ensemble fini d'équations E
un ordre <
Sortie : un système de réécriture R qui termine, qui est confluent correspondant à E, et compatible avec l'ordre < s'il en existe un
"non" ou alors boucle, s'il n'existe pas de tel système de réécriture R
completionKnuthBendixVersionNaïve(E, <)
si il existe une équation s = t dans E où s ≠ t et ni s < t, ni t < s
retourner "non"
sinon
Soit R l'ensemble des règles G → D où G = D ou D = G est une équation de E et D < G
répéter
pour toute paire critique s, t de R
s' := une R-forme normale de s
t' := une R-forme normale de t
si s' ≠ t'
si t' < s'
ajouter s' → t' à R
sinon si s' < t'
ajouter t' → s' à R
sinon
retourner "non"
tant que R a été modifié par la boucle
retourner R
Procédure de complétion sous forme de règles
On peut présenter[11] - [12] la complétion de manière synthétique à l'aide de règles d'inférence qui transforment à la fois le système d'équations et le système de réécriture. On les écrit sous la forme où le numérateur donne le système d'équations et le système de réécriture avant l'application de la règle et le dénominateur donne le système d'équations et le système de réécriture après l'application de la règle. En appliquant les règles (dans n'importe quel ordre et tant que c'est possible), on espère transformer l'état initial où il y a les équations données en entrée et un système de réécriture vide en un état final où il n'y a plus d'équations à traiter et un système de réécriture confluent et qui termine.
Règles de base
On donne d'abord un ensemble minimal de règles[13] - [14] :
| Nom de la règle | Règle | Explication |
|---|---|---|
| Orienter une identité |
si s > t |
Transforme une identité en une règle en utilisant l'ordre de réduction < |
| Déduire une identité |
s'il existe u qui se réécrit en s et qui se réécrit en t |
Ajoute une identité déduite du système de réécriture. La règle donnée ici est très générale. Un cas spécial de la règle consiste à ajouter l'identité s = t pour toute paire critique (s, t) de R. |
| Supprimer une identité triviale | Supprime une identité triviale où les termes de part et d'autre sont syntaxiquement les mêmes. | |
| Simplifier une identité |
si s se réécrit en s' ou t se réécrit en t' |
Simplifie une identité en utilisant le système de réécriture. |
On note l'invariant suivant : l'application d'une règle conserve les égalités que l'on peut démontrer en combinant les égalités de E ou les règles de réécriture de R, le système de réécriture termine toujours. Les transformations ne font que faire croître le système de réécriture R.
Règles d'optimisation
Les quatre transformations ci-dessus construisent un système de réécriture où il y a redondance des règles de réécriture et qui, étant donné un ordre de terminaison, n'est pas unique. C'est pourquoi on utilise aussi les deux règles suivantes qui sont des optimisations afin d'obtenir un système de réduction avec moins de règles, qui soit unique pour l'ordre que l'on s'est donné et qui soit plus efficace pour calculer les formes normales.
| Composer |
si t se réécrit en u |
Ajoute une règle au système de réécriture qui compose la réécriture s en t et t en u |
| Effondrement |
si s → u en utilisant une règle G → D où G ne peut pas être réduit par s → t |
Supprime une règle dont le membre gauche est simplifiable, sans la faire disparaître complètement |
Ces transformations jouent un rôle clés dans la démonstration de la correction de la procédure de complétion[3] - [5].
Exemples
Dans cette section, nous allons exécuter la procédure de Knuth-Bendix sur quelques exemples pour illustrer les cas où la complétion réussit, échoue ou boucle.
Exemple où la complétion réussit
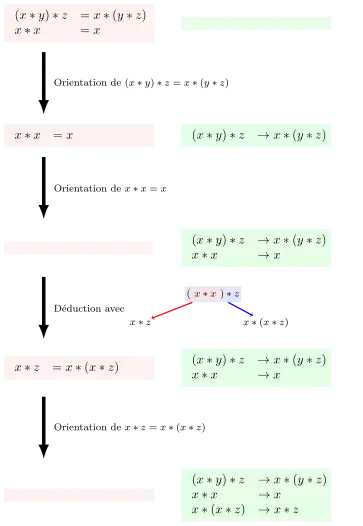
On cherche un système de réécriture confluent et qui termine pour le système d'identités pour les semi-groupes idempotents donné par :
(x * y) * z = x * (y * z)
x * x = x
La figure à droite donne les applications des règles depuis le système d'identités (et un système de réécriture vide) vers un système d'identités vide et un système de réécriture confluent et qui termine. Il y a deux premières applications des règles d'orientation. Puis une déduction d'une identité car x * z et x * (x * z) sont des paires critiques. Le système de réécriture confluent et qui termine est :
(x * y) * z → x * (y * z)
x * x → x
x * (x * z) → x * z
Exemple où la complétion échoue
Si le système d'équations contient :
x * y = y * x
alors la procédure de complétion échoue car elle n'arrive pas à orienter l'équation.
Exemple où la complétion boucle
Considérons l'exemple :
a * b = b * a
a * c = c * a = b * d = d * b = 1
Avec l'ordre lexicographique sur les chemins donné par 1 < a < c < b < d, la complétion termine. Mais avec l'ordre lexicographique sur les chemins donné par 1 < a < b < c < d, la complétion ne termine pas.
Variantes et implémentations
Il existe une implémentation de la complétion de Knuth-Bendix[15] à but pédagogique avec une interface graphique. Il existe des variantes de la complétion de Knuth-Bendix où l'ordre de complétion n'est pas donné a priori mais construit au cours du processus de complétion[16] - [17] - [18] - [19].
Le prouveur Waldmeister[20] est une implémentation de la complétion. Il a remporté les sessions de 1997 à 2011 et la session 2014 de la compétition CASC[21] dans la catégorie UEQ (pour unit-equational first-order logic).
La complétion de Knuth-Bendix est implémentée dans des outils de calculs formels par exemple Magma[22] qui utilise le package kbmag[23].
Notes et références
- D. Knuth, P. Bendix (1970). J. Leech, ed. Simple Word Problems in Universal Algebras. Pergamon Press. pp. 263–297
- L'abus de langage "algorithme" est par exemple utilisé dans le programme de la session 2015 de l'agrégation de mathématiques (option informatique) (p. 12).
- Gérard Huet: A Complete Proof of Correctness of the Knuth-Bendix Completion Algorithm. J. Comput. Syst. Sci. 23(1): 11-21 (1981)
- Une identité est une expression comprenant deux termes séparés par le symbole =. Dans la théorie que l'on considère toute instance de l'identité est affirmée être vraie. Voir l'article Identité remarquable.
- Leo Bachmair, Nachum Dershowitz: Equational Inference, Canonical Proofs, and Proof Orderings. J. ACM 41(2): 236-276 (1994)
- (en) Alfred Tarski, Undecidable Theories,
- Sam Kamin et Jean-Jacques Lévy, Attempts for generalizing the recursive path orderings (February 1st 1980).
- Nachum Dershowitz: Orderings for Term-Rewriting Systems. Theor. Comput. Sci. 17: 279-301 (1982)
- (en) Franz Baader et Tobias Nipkow, Term Rewriting and All That, Cambridge University Press, 1998 (ISBN 0521779200)
- L'ensemble des termes est infini. L'ordre < n'est pas donné explicitement mais il s'agit d'un algorithme qui nous dit si deux termes s et t sont tels que s < t ou non.
- (en) Bachmair, L., Dershowitz, N., Hsiang, J., Proc. IEEE Symposium on Logic in Computer Science, , 346–357 p., « Orderings for Equational Proofs »
- (en) N. Dershowitz, J.-P. Jouannaud, Rewrite Systems, vol. B, Jan van Leeuwen, coll. « Handbook of Theoretical Computer Science », , 243–320 p. Here: sect.8.1, p.293
- Nachum Dershowitz, « Term Rewriting Systems by “Terese” (Marc Bezem, Jan Willem Klop, and Roel De Vrijer, Eds.), Cambridge University Press, Cambridge Tracts in Theoretical Computer Science 55, 2003, Hard Cover: (ISBN 0-521-39115-6), Xxii+884 Pages », Theory Pract. Log. Program., vol. 5, , p. 284 (ISSN 1471-0684, DOI 10.1017/S1471068405222445, lire en ligne, consulté le )
- René Lalement, Logique, réduction, résolution, Paris/Milan/Barcelone, Masson, , 370 p. (ISBN 2-225-82104-6)
- Thomas Sternagel et Harald Zankl, « KBCV: Knuth-bendix Completion Visualizer », Proceedings of the 6th International Joint Conference on Automated Reasoning, Springer-Verlag, iJCAR'12, , p. 530–536 (ISBN 9783642313646, DOI 10.1007/978-3-642-31365-3_41, lire en ligne, consulté le )
- Pierre Lescanne: Computer Experiments with the Reve Term Rewriting System Generator. POPL 1983: 99-108
- Randy Forgaard A program for generating and analyzing Term Rewriting Systems, Master thesis MIT (1984) et David Detlefs, Randy Forgaard: A Procedure for Automatically Proving the Termination of a Set of Rewrite Rules. RTA 1985: 255-270
- Masahito Kurihara, Hisashi Kondo: Completion for Multiple Reduction Orderings. J. Autom. Reasoning 23(1): 25-42 (1999)
- (en) Ian Wehrman, Aaron Stump et Edwin Westbrook, Slothrop : Knuth-Bendix Completion with a Modern Termination Checker, Springer Berlin Heidelberg, coll. « Lecture Notes in Computer Science », (ISBN 978-3-540-36834-2 et 9783540368359, lire en ligne), p. 287–296
- « Waldmeister - Theorem Prover », sur people.mpi-inf.mpg.de (consulté le )
- « The CADE ATP System Competition », sur www.cs.miami.edu (consulté le )
- (en) « Magma. 4 Semigroups and Monoids. »
- (en) « Package kbmag »
Articles connexes
- Combinatoire des mots
- Paire critique
- Algorithme de Buchberger : bien que développé indépendamment, c'est une instantiation de la complétion de Knuth-Bendix pour un idéal polynomial








