Coloration fractionnaire
En théorie des graphes, la coloration fractionnaire est une généralisation de la coloration des graphes ordinaire.
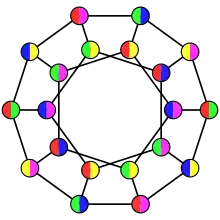
Dans une coloration de graphe traditionnelle, une couleur est affectée à chaque sommet d'un graphe, et deux sommets adjacents ne doivent pas avoir la même couleur. Dans une coloration fractionnaire, un ensemble de couleurs est affecté à chaque sommet du graphe. L'exigence relative aux sommets adjacents est toujours valable. Par conséquent, si deux sommets sont reliés par une arête, ils ne doivent pas avoir de couleurs communes.
La coloration fractionnaire de graphes peut être vue comme la relaxation linéaire de la coloration de graphes traditionnelle. En effet, les problèmes de coloration fractionnaire se prêtent beaucoup mieux à une approche de programmation linéaire que les problèmes de coloration traditionnels.
Définitions
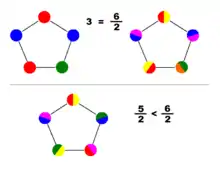
En bas : Une 5:2-coloration du même graphe.
On se donne un ensemble C de a couleurs ; une a:b-coloration d'un graphe G est l'affectation, à chaque sommet, d'un ensemble de b couleurs parmi les a couleurs de C de telle manière que les ensembles de couleurs de deux sommets adjacents sont disjoints. Si b=1, il s'agit d'une coloration au sens usuel du terme. Le b-nombre chromatique noté est le plus petit a tel qu'une a:b-coloration existe. De mainière équivalente, elle peut être définie comme un homomorphisme sur le graphe de Kneser KGa,b.
Le nombre chromatique fractionnaire est le nombre défini par
La limite existe parce que est sous-additive, autrement dit .
nombre chromatique fractionnaire
Le nombre chromatique fractionnaire peut être défini de manière équivalente en termes probabilistes : est le plus petit k pour lequel il existe une distribution de probabilité sur les ensembles indépendants de G telle que pour chaque sommet v, et pour chaque ensemble indépendant S tiré de la distribution, on a :
Propriétés
On a
- et ,
où n(G) est le nombre de sommets du graphe, est la taille maximale d'un ensemble indépendant, is the nombre de clique, et est le nombre chromatique.
En outre, le nombre chromatique fractionnaire est proche du nombre chromatique à un facteur logarithmique près[1], en fait, on a :
- .
Les graphes de Kneser sont des exemples où le rapport est arbitrairement grand, puisque alors que .
Formulation en programmation linéaire
Le nombre chromatique fractionnaire d'un graphe G peut être obtenu comme solution à un programme linéaire. Soit l'ensemble de tous les ensembles indépendants de G, et soit l'ensemble de tous les ensembles indépendants qui contiennent le sommet x. Pour chaque ensemble indépendant I, on définit une variable réelle non négative xI. Alors est la valeur minimale de
soumis à
pour chaque sommet .
Le programme dual de ce programme linéaire calcule le nombre de clique fractionnaire, une relaxation aux nombres rationnels de la notion de nombre de clique. C'est une pondération des sommets de G telle que le poids total attribué à tout ensemble indépendant est au plus 1. Le théorème de la dualité forte de la programmation linéaire garantit que les solutions optimales des deux programmes linéaires ont la même valeur. Cependant chaque programme linéaire peut avoir une taille exponentielle en fonction du nombre de sommets de G, et le calcul du nombre chromatique fractionnaire d'un graphe est NP-difficile[2]. Cela contraste avec le problème de coloration fractionnaire des arêtes d'un graphe, qui peut être résolu en temps polynomial. C'est une conséquence directe du théorème d'Edmonds des polytopes[3] - [4].
Applications
Les applications de la coloration fractionnaires de graphes comprennent la planification d'activités. Dans ce cas, le graphe G est un graphe de conflit ; en d'autres termes, une arête de G entre les nœuds u et v indique que u et v ne peuvent pas être actifs simultanément. Autrement dit, l'ensemble des nœuds qui sont actifs simultanément doit être un ensemble indépendant dans le graphe G.
Une coloration fractionnaire optimale du graphe G fournit alors un calendrier le plus court possible, de sorte que chaque nœud est actif pendant (au moins) 1 unité de temps au total, et qu'à tout moment, l'ensemble des nœuds actifs est un ensemble indépendant. Si on a une solution x au programme linéaire ci-dessus, on parcourt simplement tous les ensembles indépendants I dans un ordre arbitraire. Pour chaque I, les nœuds dans I sont actifs pour unités de temps ; pendant ce temps, chaque nœud qui n'est pas dans I est inactif.
Plus concrètement, chaque nœud de G peut représenter une transmission dans un réseau de communication sans fil ; les arêtes de G représentent les « interférences » entre les transmissions. Chaque transmission doit être active pendant une unité de temps au total ; une coloration fractionnaire optimale du graphe fournit un programme de longueur minimale (ou, de manière équivalente, un programme de largeur de bande maximale) qui est sans conflits.
Comparaison avec la coloration traditionnelle
Si l'on exige de plus que chaque nœud soit actif de manière continue pendant une unité de temps (sans pouvoir l'éteindre et le rallumer de temps en temps), alors la coloration de graphe traditionnel fournit un calendrier optimal : d'abord les nœuds de couleur 1 sont actifs pendant une unité de temps, puis les nœuds de couleur 2 sont actifs pendant une unité de temps, et ainsi de suite. Là encore, à tout moment, l'ensemble des nœuds actifs est un ensemble indépendant.
En général, la coloration fractionnaire de graphes offre un calendrier plus court que la coloration non fractionnaire des graphes ; il y a un écart de relaxation continue. Il peut être possible de trouver un calendrier plus court, au prix de l'emploi intermittent.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Fractional coloring » (voir la liste des auteurs).
- László Lovász: "On the ratio of optimal integral and fractional covers", Discrete Math. 13:4(1975), p. 383-390.
- Carsten Lund et Mihalis Yannakakis, « On the hardness of approximating minimization problems », Journal of the ACM, vol. 41, no 5, , p. 960–981 (DOI 10.1145/185675.306789).
- B. Hajek et G. Sasaki, « Link scheduling in polynomial time », IEEE Transactions on Information Theory, vol. 34, no 5, , p. 910–917 (DOI 10.1109/18.21215)
-
Alexander Schrijver, Combinatorial Optimization: Polyhedra and Efficiency, Berlin ; Heidelberg ; New York, N.Y., Springer-Verlag, (ISBN 978-3540443896, lire en ligne
 ), p.474-475
), p.474-475



















