Coefficient de vitesse

Dans l’air (ou dans un fluide dont la masse volumique peut être négligée), son libellé est :

${\displaystyle C_{V}={\frac {v}{v_{\infty }}}}$

libellé où :

${\displaystyle v}$ est la vitesse de l'écoulement au point considéré

${\displaystyle v_{\infty }}$ est la vitesse du fluide loin du corps.

Représentation graphique

Distribution des ${\displaystyle C_{p}etC_{v}}$ autour du dirigeable Akron

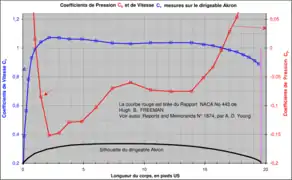
L’image ci-contre fait apparaître en bleu le coefficient de vitesse ${\displaystyle C_{V}}$ (à lire sur l'échelle de gauche) au long d’un très grand modèle du dirigeable Akron à l’incidence nulle (ce modèle mesurait 6 m de longueur).

Pour ce corps profilé, le ${\displaystyle C_{V}}$ est nul au point d'arrêt, passe par l'unité plus en aval (nettement avant le maître couple), passe par un maximum supérieur à l'unité un peu avant le maître couple (accélération maximale du flux) pour décroître peu à peu plus en aval.

Dès lors qu'on définit également le coefficient de pression adimensionnel C_p[2] - [alpha 1] :

${\displaystyle C_{p}={p-p_{\infty } \over {\frac {1}{2}}\rho _{\infty }v_{\infty }^{2}}}$

où :

${\displaystyle p}$ est la pression statique mesurée au point considéré

${\displaystyle p_{\infty }}$ est la pression statique de l’écoulement (c'est-à-dire à l’écart des perturbations créées par le corps)

${\displaystyle v_{\infty }}$ est la vitesse de l’écoulement loin du corps

${\displaystyle \rho _{\infty }}$ est la masse volumique du fluide (l’air, ici, par exemple)

on peut constater entre les deux coefficients ${\displaystyle C_{V}}$ et ${\displaystyle C_{P}}$ la relation :

${\displaystyle C_{p}=1-C_{V}^{2}}$

Cette égalité très simple constitue la variante adimensionnelle de l’équation de Bernoulli et elle est valable uniquement en dehors de la couche limite (qui s'épaissit à partir du point d'arrêt jusqu'au culot du corps).

Dans la pratique, la pression locale en un point d'un corps (et donc son C_P à ce point) est mesuré à travers la couche limite au moyen d'un orifice sur le corps (orifice qui aboutit à un manomètre) car, par chance, la pression statique locale se transmet (à très peu près) depuis le sommet de la couche limite jusqu'à la paroi du corps. Le coefficient de vitesse local ${\displaystyle C_{V}}$ (juste au-dessus de la couche limite) en est déduit par application de la variante adimensionnelle de l'équation de Bernoulli.

Il est cependant possible de mesurer également la vitesse locale de l'écoulement en un point du corps avec des micro-tubes de Pitot ou un fil chaud, mais l'on est alors confronté à la réduction de la vitesse de l'écoulement due à la présence de la couche limite.

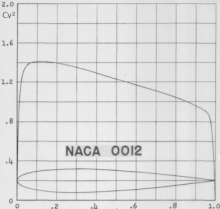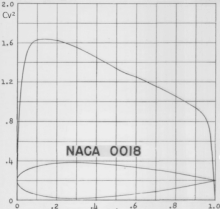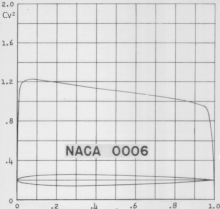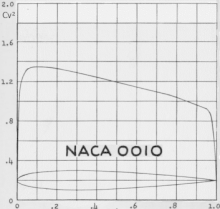
En application de la variante adimensionnelle de l'équation de Bernoulli (citée ci-dessus) le coefficient de pression ${\displaystyle C_{P}}$ est lié linéairement au carré du coefficient de vitesse ${\displaystyle C_{V}}$, c'est ce qui explique que dans le rapport NACA n^o 824 (réf. ci-dessous), ce soit le carré du ${\displaystyle C_{v}}$ qui est utilisé pour représenter la pression (animation ci-contre) :

Animation du Cv² des profils NACA 4 chiffres.