Automodulation de phase

Une impulsion (courbe du haut) qui se propage dans un milieu non linéaire subit un changement de fréquence propre (courbe du bas) dû à une automodulation de phase. Le front de l'impulsion est décalé vers des fréquences plus basses, tandis que la fin de l'impulsion tend vers des fréquences plus élevées.

Considérons une impulsion ultra-courte dont l'intensité au temps t est donnée par I(t). Si l'impulsion se propage dans un milieu matériel, l'effet Kerr optique induit un changement de l'indice de réfraction en fonction de l'intensité :

${\displaystyle n(I)=n_{0}+n_{2}\cdot I}$

où n₀ est l'indice de réfraction linéaire et n₂ l'indice de réfraction non linéaire de second ordre du milieu. Nous considérons dans toute la suite de cet article une nonlinéarité n₂ positive (comme c'est par exemple le cas dans les fibres optiques), mais il est également possible d'avoir un coefficient n₂ négatif (dans quel cas les conclusions énoncées seront opposées).

Lors de la propagation, l'intensité à chaque point du milieu traversé augmente, puis diminue au passage de l'impulsion. D'où la variation de l'indice de réfraction :

${\displaystyle {\frac {dn(I)}{dt}}=n_{2}{\frac {dI}{dt}}}$

Cette variation provoque un décalage de la phase instantanée de l'impulsion :

${\displaystyle \phi (t)=\omega _{0}t-{\frac {2\pi }{\lambda _{0}}}\cdot n(I)L}$

où ${\displaystyle \omega _{0}}$ et ${\displaystyle \lambda _{0}}$ sont respectivement la fréquence de la porteuse et la longueur d'onde (dans le vide) de l'impulsion, ${\displaystyle L}$ la distance sur laquelle l'impulsion s'est propagée.

Le décalage de phase induit un décalage en fréquence de l'impulsion. La fréquence instantanée ω(t) est donnée par

${\displaystyle \omega (t)={\frac {d\phi (t)}{dt}}=\omega _{0}-{\frac {2\pi L}{\lambda _{0}}}{\frac {dn(I)}{dt}}.}$

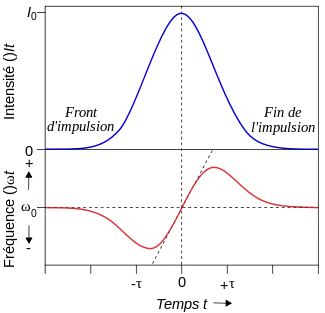
Tracer ω(t) montre la variation en fréquence de part et d'autre de l'impulsion. Le front de l'impulsion est décalé vers les basses fréquences ("décalage vers le rouge"), la traîne est décalée vers les hautes fréquences ("décalage vers le bleu"), et le sommet du pic n'est pas décalé en phase.

Dans le cas d'une impulsion symétrique (temporellement), il est clair que les fréquences supplémentaires générées par automodulation de phase élargissent le spectre en fréquence symétriquement. Dans le domaine temporel, l'impulsion ne varie pas, néanmoins dans tout milieu réel, les effets de la dispersion agiront également sur l'impulsion [2] - [3]. Dans le cas d'une dispersion normale, les plus basses fréquences (donc les plus grandes longueurs d'onde) se propagent plus rapidement que les hautes fréquences, donc le front de l'impulsion (décalé vers le rouge) se déplace plus vite que la queue (décalée vers le bleu), ce qui élargit l'impulsion également temporellement. En revanche, dans des zones à dispersion anormale, c'est l'inverse qui se produit : l'impulsion est alors comprimée temporellement, elle devient plus courte. Cet effet peut être exploité pour produire des impulsions ultra-courtes.

Illustrons le cas général en considérant une impulsion gaussienne ultra-courte de phase constante, l'intensité au temps t est donnée par I(t):

${\displaystyle I(t)=I_{0}\exp \left(-{\frac {t^{2}}{\tau ^{2}}}\right)}$

où I₀ est l'intensité maximale et τ la demi-largeur de l'impulsion.

D'où la variation de l'indice de réfraction :

${\displaystyle {\frac {dn(I)}{dt}}=n_{2}\cdot I_{0}\cdot {\frac {-2t}{\tau ^{2}}}\cdot \exp \left({\frac {-t^{2}}{\tau ^{2}}}\right).}$

La fréquence instantanée ω(t) est alors donnée par

${\displaystyle \omega (t)=\omega _{0}+{\frac {4\pi Ln_{2}I_{0}}{\lambda _{0}\tau ^{2}}}\cdot t\cdot \exp \left({\frac {-t^{2}}{\tau ^{2}}}\right).}$

Pour la portion centrale de l'impulsion gaussienne (entre ${\displaystyle t=\pm \tau /2}$), il y a une variation à peu près linéaire de la fréquence (chirp linéaire), approximée par

${\displaystyle \omega (t)=\omega _{0}+\alpha \cdot t}$

où α vaut

${\displaystyle \alpha =\left.{\frac {d\omega }{dt}}\right|_{0}={\frac {4\pi Ln_{2}I_{0}}{\lambda _{0}\tau ^{2}}}.}$

Une analyse similaire peut être faite pour toutes les formes d'impulsion, telles que la sécante hyperbolique carrée (sech²) générée par la plupart des lasers à impulsions courtes. Toutefois, l'approximation du chirp linéaire au milieu de l'impulsion n'est valable que pour les gaussiennes. Lorsque le front de l'impulsion est plus aigu (donc à gradient plus fort), la variation de fréquence peut être plus prononcée. Dans le cas d'une super-gaussienne, par exemble, le chirp est presque trois plus fort aux bords de l'impulsion que pour une gaussienne, et nul (et surtout de pente nulle) au centre de l'impulsion.

Si l'impulsion est suffisamment intense, l'élargissement spectral dû à l'automodulation de phase peut compenser exactement la compression temporelle due à la dispersion anormale. L'impulsion se propage alors de manière auto-similaire : on parle de soliton optique. C'est un cas asymptotique : si une impulsion gaussienne d'intensité suffisante est injectée dans la fibre optique non linéaire, sa forme tend vers la sécante hyperbolique correspondant à l'équilibre entre l'effet non linéaire d'automodulation de phase (qui tend à élargir le spectre) et l'effet de la dispersion anormale de la vitesse de groupe (qui tend à le rétrécir).

Pour une impulsion de profil d'intensité parabolique, la dérive de fréquence introduite sera parfaitement linéaire[4]. Pour une impulsion triangulaire, elle sera constante par morceau[5].