Arbre (combinatoire)

Deux arbres planaires différents.

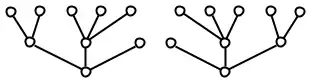
Un arbre planaire est un graphe acyclique représenté dans un plan (par un plongement) sans que les arêtes se croisent. Ces arbres sont également appelés arbres ordonnés, si de plus ils sont enracinés alors leurs arêtes sont orientées. Dans ce cas, pour chaque nœud de l'arbre, les nœuds adjacents (ou fils) sont ordonnés ; on peut ainsi parler du j-ième fils d'un nœud.

Compter le nombre d'arbres planaires revient à compter le nombre de plongements possibles dans le plan.

Arbre planaire enraciné

Les 5 arbres de Catalan (arbres planaires enracinés) de 4 nœuds. en rouge : la racine, en vert : le nœud fantôme.

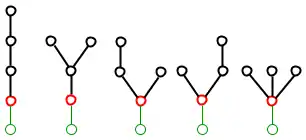
Les arbres planaires enracinés sont également appelés arbres de Catalan. Ce sont des arbres enracinés et planaires : ils possèdent une unique racine et chaque nœud engendre un ensemble ordonné de fils.

Éventuellement, la racine de l'arbre peut être jointe à un nœud fictif, ce qui justifie le terme enraciné. Dans ce cas, tous les nœuds ${\displaystyle v}$ (y compris la racine) ont un degré qui vérifie : ${\displaystyle \scriptstyle d(v)=d^{+}(v)+1}$ où ${\displaystyle \scriptstyle d^{+}(v)}$ est le nombre de fils de ${\displaystyle v}$.

Le nombre d'arbres planaires enracinés avec n≥1 nœuds est donné par le (n-1)-ième nombre de Catalan (d'où le nom de l'arbre) :

${\displaystyle C_{n-1}={\frac {1}{n}}{2n-2 \choose n-1}}$.

Un cas particulier d'arbre planaire enraciné est le cas des arbres binaires. Les nœuds d'un arbre binaire possèdent soit 2 fils (ils sont alors appelés nœuds internes), ou aucun fils (ce sont alors des feuilles). Dans un arbre binaire, il y a k nœuds internes pour k+1 feuilles. Le nombre d'arbres binaires possédant k nœuds internes (c'est-à-dire n=2k+1 nœuds) est donné par le k-ième nombre de Catalan : ${\displaystyle \scriptstyle C_{k}={\frac {1}{k+1}}{2k \choose k}}$.

Plus généralement, on peut considérer les arbres m-aires (planaires et enracinés) dont chaque nœud possède m fils. Le nombre de tels arbres possédant k nœuds internes est donné par : ${\displaystyle \scriptstyle {\frac {1}{(m-1)k+1}}{mk \choose k}}$.

Arbre planaire étiqueté

Les 20 arbres planaires enracinés étiquetés de 4 nœuds

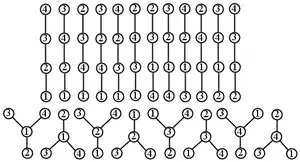
Les arbres planaires étiquetés sont des arbres et étiquetés : chacun des n nœuds de l'arbre est numéroté de 1 à n (son numéro est appelé étiquette) et engendre un ensemble ordonné de fils.

Le nombre d'arbres planaires étiquetés à n nœuds est donné par ${\displaystyle {\frac {(2n-3)!}{(n-1)!}}}$.

Arbre planaire, étiqueté et enraciné

Le nombre d'arbres planaires, étiquetés et enracinés à n nœuds est donné par : ${\displaystyle \scriptstyle {\frac {n(2n-3)!}{(n-1)!}}}$ puisque chacun des n nœuds peut être la racine de l'arbre planaire étiqueté.

Au contraire des arbres planaires, l'ensemble des fils des nœuds d'un arbre (libre ou non planaire, ou arbre tout court) ne possède pas de structure d'ordre. Ces arbres sont aussi appelés arbres de Pólya.

Il n'existe pas de formule récursive directe pour compter les arbres enracinés et non enracinés (libre et non étiquetés). On utilise alors les fonctions génératrices et la combinatoire de Pólya, d'où le nom des arbres. On note ${\displaystyle \scriptstyle t_{n}}$ le nombre d'arbres enracinés à n nœuds et ${\displaystyle \scriptstyle {\tilde {t}}_{n}}$ le nombre d'arbres non enracinés à n nœuds. Leurs premières valeurs sont :

		n=1	n=2	n=3	n=4	...
${\displaystyle \displaystyle t_{n}=}$		1	1	2	4	...
${\displaystyle {\tilde {t}}_{n}=}$		1	1	1	2	...

${\displaystyle \displaystyle t_{1}=1,}$ ${\displaystyle \displaystyle t_{2}=1,}$ ${\displaystyle \displaystyle t_{3}=2,}$ ${\displaystyle \displaystyle t_{4}=4,}$

${\displaystyle {\tilde {t}}_{1}=1,}$ ${\displaystyle {\tilde {t}}_{2}=1,}$ ${\displaystyle {\tilde {t}}_{3}=1,}$ ${\displaystyle {\tilde {t}}_{4}=2,}$

Les fonctions génératrices correspondantes sont définies par :

${\displaystyle t(x)=\sum _{n\geq 1}t_{n}x^{n}\;\;\;\;{\hbox{et}}\;\;\;\;{\tilde {t}}(x)=\sum _{n\geq 1}{\tilde {t}}_{n}x^{n}}$.

Ces fonctions vérifient[1] les formules suivantes :

${\displaystyle t(x)=x\exp \left(t(x)+{\frac {1}{2}}t(x^{2})+{\frac {1}{3}}t(x^{3})+...\right)}$,

${\displaystyle {\tilde {t}}(x)=t(x)-{\frac {1}{2}}t(x)^{2}+{\frac {1}{2}}t(x^{2})}$.

Arbre étiqueté (arbre couvrant)

Les 16 arbres étiquetés (non planaires) à 4 nœuds.

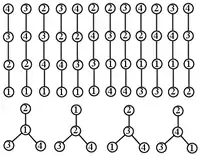
Les arbres étiquetés (non planaires) sont parfois appelés arbres de Cayley. Chaque nœud d'un arbre à n nœuds est étiqueté par une étiquette allant de 1 à n. De tels arbres peuvent être interprétés comme les arbres couvrants d'un graphe complet à n nœuds. Le nombre de tels arbres est donné par la formule de Cayley : ${\displaystyle n^{n-2}}$.

Arbre étiqueté et enraciné

Le nombre d'arbres à n nœuds, étiquetés et enracinés est ${\displaystyle n^{n-1}}$ puisque chacun des n nœuds peut-être la racine de l'arbre étiqueté.