Arbelos

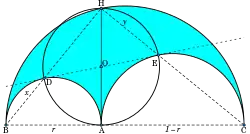
Le couteau du savetier.

Soit un demi-cercle de diamètre BC. Soit A un point quelconque de ce diamètre.

• Tracer le demi-cercle de diamètre BA intérieur.
• Tracer le demi-cercle de diamètre AC intérieur.
• Considérer la surface intérieure obtenue : c'est une lame d'arbelos.

Cette figure possède de nombreuses propriétés, en voici quelques-unes :

Propriété de l'aire : soit AH la demi-corde verticale passant par A. L'aire de l'arbelos est égale à l'aire du cercle de diamètre AH.

Démonstration : il suffit d'appeler b et c les diamètres AB et AC, et h la hauteur AH. Les aires des demi-cercles sont alors respectivement de ${\displaystyle {\pi \over 8}b^{2}}$, ${\displaystyle {\pi \over 8}c^{2}}$, ${\displaystyle {\pi \over 8}(b+c)^{2}}$. Puis, par différence, on obtient l'aire de l'arbelos ${\displaystyle {\pi \over 4}bc}$. La dernière étape fait appel aux propriétés du triangle rectangle dans lequel le carré de la hauteur est égal au produit des longueurs découpées sur l'hypoténuse. En d'autres termes : ${\displaystyle bc=h^{2}}$. Ce qui nous donne pour l'aire de l'arbelos : ${\displaystyle {\pi \over 4}h^{2}}$ qui est bien l'aire du cercle de diamètre AH.

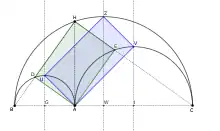
Deux rectangles formés dans un arbelos

Propriété du rectangle : Le segment BH coupe le demi-cercle BA en D. Le segment CH coupe le demi-cercle AC en E. Alors DHEA est un rectangle.

Démonstration : Les triangles BDA, BHC et AEC sont rectangles car inscrits dans des demi-cercles (théorème de Thalès (cercle)). Le quadrilatère ADHE possède donc trois angles droits, c'est un rectangle.

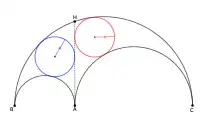
Autre propriété : les cercles inscrits aux deux parties d'un arbelos, séparés par la tangente aux cercles intérieurs, ont même rayon.

Propriété des tangentes : La droite (DE) est une tangente commune aux deux cercles.

Démonstration : La similitude de centre D qui envoie B sur A a pour angle ${\displaystyle \pi /2}$ et envoie aussi A sur H (les triangles DBA et DAH sont semblables). Elle envoie donc le milieu I de [AB] sur le milieu O de [AH] et l'angle IDO est droit. La droite (DO) est donc tangente au premier cercle en D. Comme ADHE est un rectangle, le point O est sur (DE) donc (DE) est une tangente du premier cercle. Elle est tangente du second par un raisonnement analogue.

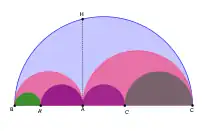
Autre propriété : dans un arbelos, en le reproduisant par homothétie dans les arcs intérieurs, les arcs touchant la tangente intérieure (ici en violet) sont égaux.