Antiprisme pentagonal
En géométrie, l'antiprisme pentagonal est le troisième solide de l'ensemble infini des antiprismes. Celui-ci peuvent être regardé comme un prisme pentagonal dont on a opéré une fraction de tour sur une des deux faces supérieure ou inférieure pour faire coïncider un sommet avec le milieu de l'arête correspondante. Ce qui a pour résultat une suite de triangles en nombre pair sur les côtés, et deux faces pentagonales supérieure et inférieure.
| Antiprisme pentagonal uniforme | |
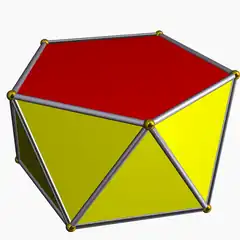
| |
| Type | Polyèdre semi-régulier |
|---|---|
| Éléments | F=12, A=20, S=10 (χ=2) |
| Faces par côtés | 10{3}+2{5} |
| Symbole de Schläfli | s{2,5} |
| Symbole de Wythoff | | 2 2 5 |
| Coxeter-Dynkin | |
| Symétrie | D5d (en) |
| Références | U77(c) |
| Dual | Trapézoèdre pentagonal |
| Propriétés | convexe |
 Configuration de sommet 3.3.3.5 | |
Si toutes ses faces sont régulières, c'est un polyèdre semi-régulier.
Voir aussi
- Ensemble des antiprismes
- Octaèdre, l'antiprisme triangulaire
- Antiprisme hexagonal
- Antiprisme octogonal
- Antiprisme décagonal
- Antiprisme dodécagonal
Liens externes
- Virtual Reality Polyhedra www.georgehart.com: L'encyclopédie des polyèdres
- VRML model
- Notation de Conway pour les polyèdres Essayer : "A5"
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.