Antiparallélogramme
L'antiparallélogramme ou contre-parallélogramme est un quadrilatère croisé dont les côtés non adjacents sont de même longueur.

Un antiparallélogramme.
Ce n'est pas un parallélogramme : il a deux côtés opposés qui ne sont pas parallèles et même, qui se coupent.
Propriétés
- Dans un antiparallélogramme les angles opposés ont la même mesure.
- Les diagonales sont parallèles.
- L'antiparallélogramme admet un axe de symétrie qui est la médiatrice des diagonales.
- Les deux côtés opposés les plus longs ont leur point d'intersection situé sur cette médiatrice.
- Son enveloppe convexe est délimitée par le trapèze isocèle formé des deux côtés non croisés et des diagonales.
- L'antiparallélogramme est inscriptible dans un cercle.
Figure articulée
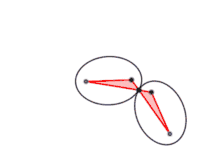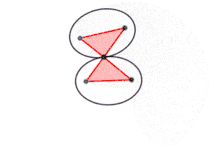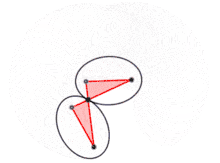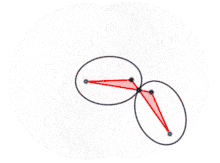
Si les sommets A, B, C et D sont articulés, la figure varie, mais le produit AC×BD reste constant.
Cette constante est égale à L2 – l2.
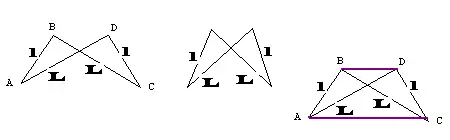
On le démontre en considérant la puissance du point C par rapport au cercle de centre B passant par A.
Lorsque les sommets A et C sont fixes, le point d'intersection des segments [AD] et [BC] parcourt une ellipse quand l'antiparallélogramme se déforme. Cette propriété a été utilisée par Frans van Schooten pour concevoir un ellipsographe[1].
Notes et références
- (la) Frans van Schooten, De Organica Conicarum Sectionum In Plano Descriptione, Tractatus. Geometris, Opticis; Præsertim verò Gnomonicis et Mechanicis Utilis. Cui subnexa est Appendix, de Cubicarum Æquationum resolutione, (lire en ligne), p. 49;50/69;70.
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.