Équation de Starling

Schéma du modèle Starling classique. À noter que la concentration de solutés interstitiels (orange) augmente avec la distance de l'artériole.

L'équation classique de Starling est la suivante[9] :

${\displaystyle \ J_{v}=L_{\mathrm {p} }S([P_{\mathrm {c} }-P_{\mathrm {i} }]-\sigma [\pi _{\mathrm {p} }-\pi _{\mathrm {i} }])}$

avec :

• ${\displaystyle J_{v}}$ le débit volumique de filtration trans-endothéliale du solvant (unités SI de m³·s ^-1 ).
• ${\displaystyle [P_{\mathrm {c} }-P_{\mathrm {i} }]-\sigma [\pi _{\mathrm {p} }-\pi _{\mathrm {i} }]}$ le différentiel de pression net total (unités SI de Pa = kg·m⁻¹·s⁻², souvent exprimé en mmHg),
  • ${\displaystyle P_{c}}$ la pression hydrostatique dans le capillaire
  • ${\displaystyle P_{i}}$ la pression hydrostatique interstitielle
  • ${\displaystyle \pi _{p}}$ la pression oncotique des protéines plasmatiques
  • ${\displaystyle \pi _{i}}$ la pression oncotique interstitielle
  • ${\displaystyle \sigma }$ le coefficient de réflexion de Staverman (adimensionnel)
  • ${\displaystyle L_{p}}$ la conductivité hydraulique de la membrane (unités SI de m²·s·kg⁻¹, équivalent à m·s ⁻¹·mmHg ⁻¹ )
  • ${\displaystyle S}$ la surface de filtration (unités SI de m² )

On définit le produit ${\displaystyle L_{p}}$ · ${\displaystyle S}$ comme le coefficient de filtration (unités SI de m⁴·s·kg⁻¹, ou de manière équivalente en m³·s⁻¹·mmHg⁻¹). L'équation de Starling donne donc une forme linéaire entre la différence de pression totale régnant entre le compartiment vasculaire et l'interstitium d'une part, et le débit volumique à travers la paroi de l'autre, avec comme constante de proportionnalité le coefficient de filtration qui agrège la surface de l'endothélium et sa conductivité. Cette forme est retrouvée dans la loi de Darcy, qui exprime le débit d'un fluide filtrant à travers un milieu poreux. Dans la loi de Darcy cependant, le terme de pression concerne uniquement les pressions hydrostatiques, et les effets de la gravité et de la viscosité du fluide sont pris en compte.

Par convention, la pression vers l'interstitium est définie comme positive et la pression vers le capillaire est définie comme négative, de sorte que J_v est positif quand le solvant sort du capillaire (filtration), et négatif quand le solvant pénètre dans le capillaire (absorption).

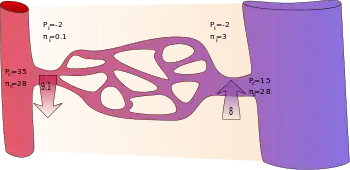
En appliquant l'équation classique de Starling, on a longtemps enseigné que les capillaires continus filtrent le liquide dans leur section artériolaire et en réabsorbent la majeure partie dans leur section veinulaire, comme le montre le diagramme[10].

Cependant, des preuves empiriques montrent que, dans la plupart des tissus, le flux du fluide intraluminal des capillaires est continu et consiste principalement en une filtration (effluent) vers l'interstitium. Cet efflux se produit sur toute la longueur d'un capillaire. Le liquide filtré vers l'espace à l'extérieur d'un capillaire est alors principalement renvoyé à la circulation par le système lymphatique et le canal thoracique[11].

Un mécanisme de ce phénomène est le modèle de Michel-Weinbaum, en l'honneur de deux scientifiques qui, indépendamment, ont décrit la fonction de filtration du glycocalyx. En bref, l'effet de la pression osmotique colloïdale ${\displaystyle \pi _{i}}$ du liquide interstitiel sur ${\displaystyle J_{v}}$ s'est avérée très mineur. La différence de pression osmotique colloïdale qui s'oppose à la filtration est maintenant connue comme étant ${\displaystyle \pi _{p}-\pi _{subglycocalix}}$, (avec ${\displaystyle \pi _{subglycocalix}}$ la pression oncotique liée au subglycocalix) qui a typiquement une valeur très faible. Pourtant, il y a dans des conditions normales une filtration suffisante pour éliminer les protéines interstitielles de la fente interendothéliale. Par conséquent, les valeurs de ${\displaystyle J_{v}}$ ainsi calculées sont beaucoup plus faibles. Quand le débit volumique de filtration baisse, les protéines interstitielles diffusent librement vers l'espace sous-glycocalix, ce qui efface la différence de pression osmotique colloïde nécessaire à la réabsorption du fluide vers le capillaire[9].

L'équation révisée de Starling est compatible avec le principe de Starling en régime stationnaire:

${\displaystyle \ J_{v}=L_{\mathrm {p} }S([P_{\mathrm {c} }-P_{\mathrm {i} }]-\sigma [\pi _{\mathrm {p} }-\pi _{\mathrm {g} }])}$

avec :

• ${\displaystyle J_{v}}$ le débit volumique de filtration trans-endothéliale du solvant (unités SI de m³·s ^-1 ).
• ${\displaystyle [P_{\mathrm {c} }-P_{\mathrm {i} }]-\sigma [\pi _{\mathrm {p} }-\pi _{\mathrm {i} }]}$ est la pression motrice nette (unités SI de Pa = kg·m⁻¹·s⁻², souvent exprimée en mmHg),
  • ${\displaystyle P_{c}}$ la pression hydrostatique dans le capillaire
  • ${\displaystyle P_{i}}$ la pression hydrostatique interstitielle
  • ${\displaystyle \pi _{p}}$ la pression oncotique des protéines plasmatiques
  • ${\displaystyle \pi _{g}}$ la pression oncotique du sous-glycocalix
  • ${\displaystyle \sigma }$ le coefficient de réflexion de Staverman (adimensionnel)
  • ${\displaystyle L_{p}}$ la conductivité hydraulique de la membrane (unités SI de m²·s·kg⁻¹, équivalent à m·s ⁻¹·mmHg ⁻¹ )
  • ${\displaystyle S}$ la surface de filtration (unités SI de m² )

Les pressions sont souvent mesurées en millimètres de mercure (mmHg) et le coefficient de filtration en millilitres par minute par millimètre de mercure (ml·min ^-1·mmHg^-1).

Valeurs approximatives

Voici les valeurs généralement utilisées pour les variables de l'équation classique de Starling :

Emplacement	${\displaystyle P_{c}}$ (mmHg) [16]	${\displaystyle P_{i}}$ (mmHg) [16]	${\displaystyle \sigma \cdot \pi _{c}}$ (mmHg) [16]	${\displaystyle \sigma \cdot \pi _{i}}$ (mmHg) [16]
extrémité artériolaire du capillaire	+35	-2	+28	+0.1
extrémité veinulaire du capillaire	+15	-2	+28	+3

On suppose que de l'albumine s'échappe des capillaires et pénètre dans le liquide interstitiel où elle produirait un débit d'eau équivalent à celui produit par une pression hydrostatique de +3 mmHg. Ainsi, la différence de concentration en protéines produirait un écoulement de liquide dans le vaisseau à l'extrémité veineuse équivalent à 28 − 3 = 25 mmHg de pression hydrostatique. La pression oncotique totale présente à l'extrémité veineuse peut être considérée comme +25 mmHg.

Au début (extrémité artériolaire) d'un capillaire, il existe une pression motrice nette ( ${\displaystyle [P_{\mathrm {c} }-P_{\mathrm {i} }]-\sigma [\pi _{\mathrm {c} }-\pi _{\mathrm {i} }]}$ ) vers l'extérieur du capillaire de +9.1 mmHg. À son extrémité veinulaire, la pression motrice nette est de -8 mmHg.

En supposant que la force motrice nette diminue linéairement le long du capillaire, la pression motrice nette moyenne est dirigée vers l'extérieur du capillaire dans son ensemble, ce qui a également pour résultat que plus de fluide sort d'un capillaire qu'il n'y rentre. C'est alors le système lymphatique qui draine l'excès résultant.

J. Rodney Levick soutient dans son manuel que la pression interstitielle est souvent sous-estimée, et les mesures qui y sont utilisées pour remplir l'équation révisée de Starling montrent que les forces d'absorption sont systématiquement inférieures aux pressions capillaires ou veinulaires.

Les principes qui sous-tendent l'équation sont utiles pour expliquer les phénomènes physiologiques dans les capillaires, tels que la formation d'œdème[3] - [4].

Woodcock et Woodcock ont montré en 2012 que l'équation révisée de Starling (principe de Starling à l'état stationnaire) fournit des explications scientifiques aux observations cliniques concernant la thérapie par fluide intraveineux[18].

L'équation de Starling porte le nom du physiologiste britannique Ernest Starling, qui est également reconnu pour la loi Frank-Starling du cœur[19]. On peut attribuer à Starling d'avoir identifié que « l'absorption des solutions salines isotoniques (de l'espace extravasculaire) par les vaisseaux sanguins est déterminée par cette pression osmotique des protéines sériques » en 1896[2].

• Fonction rénale

• (en) Derangedphysiology.com : Principe de Starling de la dynamique des fluides transvasculaires : Starling forces and fluid exchange in the microcirculation