Énigme des trois maisons
L'énigme des trois maisons, aussi appelée l'énigme de l'eau, du gaz et de l'électricité, est un jeu mathématique dont l'analyse utilise un théorème de topologie ou de théorie des graphes. Ce problème n'a pas de solution. Georges Perec le cite en 1978 dans son livre Je me souviens : « Je me souviens des heures que j'ai passées, en classe de troisième, je crois, à essayer d'alimenter en eau, gaz et électricité, trois maisons, sans que les tuyaux se croisent (il n'y a pas de solution tant que l'on reste dans un espace à deux dimensions ; c'est l'un des exemples élémentaires de la topologie, comme les ponts de Königsberg, ou le coloriage des cartes) »[1] - [Note 1].
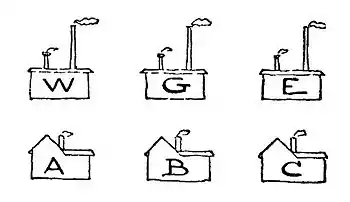
Cette énigme est déjà posée par Henry Dudeney en 1917 dans son livre Amusements in mathematics. Il précise qu'« il existe une demi-douzaine d'énigmes vieilles comme le monde, qui réapparaissent perpétuellement[2] ». Celle de l'article en est une, qu'il appelle eau, gaz, et électricité[2]. Elle est popularisée par Martin Gardner, qui la présente dans son Sixième livre de jeux mathématiques[3].
Il existe deux approches pour démontrer l'inexistence d'une solution connectant chacune des trois maison directement aux trois fournisseurs. La première approche montrant l'impossibilité utilise le théorème de Jordan, indiquant que si l'on dessine une boucle dans un plan, le complémentaire de la boucle, c'est-à-dire la partie non dessinée du plan, se compose de deux connexes par arcs, l'un borné (l'intérieur de la boucle) et l'autre non (l'extérieur de la boucle). La seconde approche, plus générale, utilise la formule d'Euler pour les graphes planaires. Elle est une étape dans la démonstration du théorème clé des graphes planaires, due à Kazimierz Kuratowski.
Énoncés
.svg.png.webp)
Sous la forme d'historiette, l'énigme s'exprime de la manière suivante[4] :
« Un lotissement de trois maisons doit être équipé d'eau, de gaz et d'électricité. La règlementation interdit de croiser les canalisations pour des raisons de sécurité. Comment faut-il faire[5] ? »
L'historiette possède de nombreuses variantes[Note 2]. On trouve par exemple celle-ci : « Il possède… 3 voitures, lesquelles doivent pouvoir se garer indifféremment sur les places de parking 1, 2 ou 3… Il voudrait tracer des routes reliant chaque voiture à chacun des emplacements (soit un total de 9 routes distinctes) afin que chaque véhicule puisse se rendre sur n'importe laquelle de ces places, mais, afin d'éviter les collisions, ces chemins ne doivent en aucun cas se couper, ni être confondus (même partiellement). Ces chemins peuvent passer derrière les parkings et les autos, et avoir n'importe quelle forme, mais ne doivent pas traverser les emplacements (ni bien sûr les autres véhicules) »[6].
Ce problème peut aussi être vu de façon abstraite comme un graphe, ce qui permet de l'étudier mathématiquement. Un graphe est composé d'un ensemble de points, appelés nœuds ou sommets, dont certains sont reliés par des liens (également appelés arêtes). Dans le cas de l'énigme, il existe deux ensembles de nœuds : l'ensemble M ayant trois nœuds pour les trois maisons (en bleu dans la figure ci-contre), et l'ensemble F ayant trois nœuds pour l'arrivée de gaz, d'eau et d'électricité (en rouge dans la figure ci-contre). L'énigme demande qu'il existe un lien entre chaque nœud de M et chaque nœud de F, de façon telle que deux liens ne se croisent pas : une façon possible de disposer ces liens est montrée dans la figure ci-contre avec les liens en vert. Un graphe dans lequel tous les nœuds d'un ensemble de m éléments doivent être reliés à ceux d'un ensemble de n élément est appelé graphe biparti complet, noté Km,n. Un graphe dans lequel deux liens ne se croisent pas est appelé planaire. La question devient : K3,3 est-il un graphe planaire ?
Topologie géométrique
Préambule
.jpg.webp)
.jpg.webp)
Une première démarche, pour élucider l'énigme, consiste à faire des essais. Elle débouche sur un double constat. Rapidement, celui qui cherche à résoudre l'énigme y arrive presque, c'est-à-dire qu'il parvient à poser huit canalisations, mais la dernière résiste. Le deuxième constat est qu'il existe beaucoup de possibilités différentes à tester.
Intuitivement, il semble évident que certaines d'entre elles sont équivalentes. Deux tentatives telles qu'il est possible de déformer continument les canalisations pour passer de la première à la seconde correspondent en fait à la même tentative. Cette équivalence porte un nom en mathématique, elle s'appelle l'homotopie. Il s'avère que cette notion, difficile à formaliser précisément, n'est guère nécessaire pour résoudre l'énigme[7]. Malgré cette remarque, il reste encore une grande quantité de tentatives possibles. La canalisation reliant la première maison au gaz (en suivant l'ordre proposé dans l'illustration du paragraphe Énoncés) peut passer entre l'eau et l'électricité, mais aussi passer entre la première maison et le fournisseur d'eau, ou encore passer par en dessous et contourner par le bas les deuxième et troisième maisons.
Un rapide examen permet de conclure qu'il existe une infinité de possibilités. La canalisation qui relie la première maison et l'électricité peut commencer par faire n fois le tour des trois maisons puis rejoindre l'électricité. Ces n tours n'offrent aucun espoir de solution, mais, au premier regard, il ne semble pas simple de trouver un bon critère permettant d'éliminer les tentatives inutiles, ce qui rend l'énigme un peu déroutante. Passer en revue une infinité de possibilités n'est guère praticable[Note 3].
Toutes les tentatives de cette nature débouchent au mieux par la pose de huit canalisations, puis il devient impossible d'aller plus loin. Ce point commun peut laisser penser que la bonne démarche consiste à procéder d'un raisonnement différent. Cette bonne démarche se fonde sur un concept et un théorème suffisamment intuitif pour qu'une démonstration ne soit pas jugée envisageable[8] avant le XIXe siècle. Une réflexion plus approfondie montre qu'il n'en est rien et qu'ils suffisent à bâtir une preuve aisément compréhensible de l'inexistence d'une solution.
Ensemble connexe par arcs

Le concept clé de la démonstration est la connexité. Une illustration du concept est donné par l'archipel des Canaries dans l'image ci-contre. Une île est connexe par arcs, c'est-à-dire que pour tout couple de points de l'île, il existe un chemin allant d'un point à l'autre sans quitter l'île. En revanche, la réunion de deux îles n'est pas connexe par arcs : il n'existe pas de chemins permettant de se rendre entre deux points sans se mouiller, s'ils sont sur deux îles différentes. Une île est une composante connexe par arcs : c'est un ensemble maximal de points entre lesquels il existe un chemin. Un archipel consiste ainsi en plusieurs composantes connexes par arcs, soit 5 dans l'image ci-contre.
En termes mathématiques, si A est un ensemble muni d'une topologie et si, pour deux points quelconque de A, il existe un chemin dans A qui relie les deux points, A est dit connexe par arcs.
Un second concept est celui de frontière. Sur l'exemple de l'archipel, la frontière correspond au littoral, c'est-à-dire à l'ensemble des points qui touchent en même temps une île et la mer. En termes plus mathématiques, un point est à la frontière d'un ensemble E lorsqu'un disque centré en ce point et de rayon strictement positif, touche à la fois l'ensemble E et son complémentaire.
Théorème de Jordan
.jpg.webp)
Le théorème clé de la démonstration est encore plus déroutant de simplicité apparente. En substance, il indique qu'il n'est pas possible d'aller de la Suisse à la France sans traverser la frontière. Pour l'énoncer en termes plus mathématiques, un peu de vocabulaire n'est pas inutile.
Pour établir la démonstration, il faut introduire la notion de courbe de Jordan, aussi appelée lacet simple. Cette courbe est une ligne continue dans le plan, qui ne se croise pas. Dans la figure de droite, la frontière en noir est un exemple d'une courbe de Jordan. Un cercle est aussi une courbe de Jordan, puisqu'il s'agit toujours d'une ligne continue sans croisement. En revanche, un 8 ne l'est pas puisqu'il y a croisement au centre du 8.
Le théorème de Jordan traite du complémentaire d'une courbe de Jordan S. Le théorème considère la partie du plan qui ne contient pas S. Il indique que ce complémentaire contient deux composantes connexes par arcs, dont la frontière est la courbe S. Sur l'exemple ci-contre, une composante est en bleu tandis que l'autre est en rouge, et la frontière est en noir. Bien que le résultat semble intuitivement évident, sa démonstration ne l'est pas. En effet, il a fallu plus d'un demi-siècle pour l'obtenir. L'élément clé du théorème réside dans la définition de connexité de la section précédente : considérons un point a dans la zone bleue et un point b dans la rouge. Si l'on souhaite se rendre de a à b, il est nécessaire de sortir de la zone bleue, et une frontière est traversée. De même façon, la France peut correspondre à une composante connexe par arcs, la Suisse à une autre, et il n'est pas possible d'aller d'une ville en Suisse à une ville en France sans traverser la frontière. Raisonner en termes de composantes connexes par arcs et de frontière, ou encore d'îles et de littoral permet d'éviter la complexité combinatoire.
Placement des six premières canalisations
.jpg.webp)
.jpg.webp)
Poser une canalisation revient à interdire une zone de l'espace. Si un jeu de canalisation forme une boucle, les idées précédentes sont applicables. On peut, en dessinant la solution sur une feuille de papier, découper les deux zones séparées, bien les éloigner et tenter de résoudre l'énigme sur les différentes îles ainsi obtenues.
Le principe du raisonnement est par l'absurde. On suppose qu'il existe une solution, on montre que cette existence contredit le théorème de Jordan. On en déduit qu'elle ne peut exister car le théorème de Jordan n'est jamais contredit. On utilise les notations suivantes : M1, M2, M3 désignent les trois maisons, F1 le fournisseur d'eau, F2 celui d'électricité et F3 celui de gaz.
Le premier objectif consiste à séparer l'espace en deux composantes connexes par arcs, c'est-à-dire à créer deux îles distinctes. Comme on suppose qu'une solution existe, il est possible de considérer la canalisation reliant M1 à F1, à laquelle on adjoint celle reliant F1 à M2, à laquelle on adjoint celle reliant M2 à F2, adjointe à F2 à M3, puis M3 à F3, puis F3 à M1. Elles sont illustrées sur la figure de gauche. On obtient une courbe de Jordan contenant, dans l'ordre, les points M1, F1, M2, F2, M3, F3 puis à nouveau M1. Si rien ne nous assure que la configuration solution de l'énigme (que l'on suppose exister) est effectivement celle de gauche, nous savons au moins une chose : ces canalisations forment une courbe de Jordan contenant dans l'ordre précédent, les trois maisons et les trois fournisseurs.
Cette courbe divise le plan en deux composantes connexes par arcs, que l'on peut considérer comme deux îles éloignées. Chacune de ces deux composantes connexes par arcs possède une frontière contenant toutes les maisons et tous les fournisseurs. Chacune de ces deux composantes connexes par arcs est analogue à la figure de droite. Analogue signifie ici que les ensembles sont connexes par arcs et de même frontière.
Si le résultat ne semble pas choquant pour la composante bleue, il peut paraître plus surprenant pour la rose. La composante rose correspond plus à un continent infiniment vaste percé par une mer intérieure qu'à une île. Comme les deux éléments clés sont la connexité et la frontière, cela n'a guère d'importance. Pour s'en persuader, on peut imaginer cette transformation du plan appelée inversion, qui laisse invariant le cercle, transforme l'intérieur en extérieur et vice-versa. Cette transformation ne traite pas le centre du cercle. Mais, pour l'énigme, ajouter un point isolé ne change rien quant à l'existence ou non d'une solution. Il est aisé de le contourner, par la droite ou la gauche. Une autre manière de voir les choses est d'imaginer résoudre l'énigme sur la sphère et non pas le plan. En plaçant la courbe de Jordan sur l'équateur, la similitude entre les deux îles devient évidente. La figure en bas à droite montre qu'une sphère sans son pôle nord peut être vue, à l'aide d'une projection stéréographique, comme un plan. Les deux énigmes sur un plan ou une sphère sont donc équivalentes.
Conclusion
.jpg.webp)
À partir de maintenant, la pose de toute nouvelle canalisation se traduit par un coup de ciseau qui engendre une nouvelle île. Cette fragmentation de l'espace est à l'origine de l'impossibilité. L'intérêt d'une telle démarche est qu'elle évite toute combinatoire. Comme le montre le paragraphe précédent, prise dans le bon ordre, les six premières poses sont, d'un certain point de vue, forcées. Quelle que soit la manière dont on s'y prend, la pose des six premières canalisations débouche toujours sur la même configuration topologique. À condition de décomposer l'espace en îles telles que le littoral contiennent les nœuds (maisons et fournisseurs), il est possible de se limiter à l'étude d'une unique configuration, pour la suite du raisonnement.
La canalisation fournissant en électricité la première maison est dans l'une des deux composantes connexes par arcs du paragraphe précédent. Notons là A. Cette composante A contient une ligne reliant M1 à F2, située à l'intérieur de A composée de points soit tous roses soit tous bleus, mais jamais vert. On obtient une nouvelle courbe de Jordan composée de la ligne M1F2, puis des lignes F2M3F3M1. Finalement, on obtient la ligne M1F2M3F3M1. Elle définit une nouvelle composante connexe par arcs, notée A1. On peut se demander si cette nouvelle île contient les points F1 et M2. On sait déjà qu'ils ne sont pas sur la ligne F2M3F3M1. Ils ne peuvent pas non plus se situer sur la ligne M1F2 car cette ligne se situe à l'intérieur de A, c'est-à-dire dans l'île A et non pas sur le littoral, or les points F1 et M2 ne sont pas situés sur l'île à proprement parler mais sur la frontière. La même raison indique qu'ils ne peuvent pas non plus se situer à l'intérieur de A1. On obtient de même une île A2, dont la frontière est formée des canalisations reliant : M1F1M2F2M1. Le théorème de Jordan nous assure encore que ces deux zones sont bien des îles distinctes, c'est-à-dire des composantes connexes par arcs disjointes.
L'espace est maintenant fragmenté en trois îles, dont deux ne contiennent plus que quatre nœuds. Posons maintenant la canalisation qui relie la deuxième maison au gaz. Elle est située dans l'une des trois composantes connexes par arcs. Cette composante connexe par arcs possède une frontière contenant à la fois M2 et F3. Ni A1 ni A2 ne possède cette propriété. C'est donc la composante connexe par arcs qui n'a pas été découpée par la canalisation reliant M1 à F2 qui contient cette canalisation. Une fois encore, avec le point de vue adopté, le coup est forcé. Si l'on note B1 et B2 ces deux nouvelles composantes connexes par arcs, elles ont toutes deux comme frontière une courbe de Jordan et leurs frontières passent, pour B1 par les points M1F1M2F3M1 et pour B2 par M2F2M3F3M2.
L'espace est maintenant fragmenté en quatre îles, les fournisseurs et les maisons se trouvent toutes sur le littoral et aucune île n'en contient plus de quatre. De plus, on connaît, pour chaque île la nature exacte des fournisseurs et des maisons présentes sur le littoral. Il s'agit maintenant de relier la troisième maison à l'eau. Un rapide passage en revue des différentes frontières montre qu'aucune d'elles ne contient à la fois la troisième maison M3 et l'eau F1.
Cette dernière canalisation parcourt au moins deux composantes connexes par arcs (c'est-à-dire passe d'une île à l'autre sans passer par la mer). Ce résultat est en contradiction avec le théorème de Jordan. Elle termine la démonstration par l'absurde[9].
Théorie des graphes
.jpg.webp)
Cette énigme entre dans la branche mathématique appelée théorie des graphes et peut se traiter par la formule d'Euler. Cette formule est un ingrédient de la démonstration du théorème fondamental des graphes planaires. Un graphe est un ensemble de points, parfois appelés nœuds ou sommets, reliés entre eux par des arêtes ou des liens[10]. Un graphe est dit « planaire » s'il est possible de le représenter dans un plan. Deux liens ne peuvent se croiser qu'à l'emplacement d'un nœud. Tous les graphes ne sont pas planaires, cette énigme fournit un contre-exemple. L'origine de l'étude des graphes planaires provient d'un désir de démonstration du théorème des quatre couleurs au milieu du XIXe siècle[11]. Le théorème clé est l'œuvre de Kazimierz Kuratowski et date de 1930 : il caractérise, parmi les graphes, ceux qui sont planaires, et s'applique donc au cas particulier de l'énigme[12].
Pour comprendre les raisonnements de la théorie des graphes, une définition est utile. Une face d'un graphe planaire est une composante connexe par arcs du complémentaire du graphe dans le plan. Chaque face possède une frontière composée par des arêtes, le nombre de ces arêtes est appelé le degré d'une face. Si f désigne le nombre de faces du graphe, n son nombre de nœuds et a le nombre d'arêtes, la formule d'Euler affirme que, pour un graphe planaire connexe non vide[Note 4] :
(Un graphe est connexe s'il existe toujours un ensemble d'arêtes permettant d'aller d'un nœud à un autre.) Par ailleurs, un rapide calcul montre que la somme des degrés des différentes faces est égale à deux fois le nombre d'arêtes dans un graphe coplanaire. Or dans la situation des trois maisons, toute courbe de Jordan délimitant une face passe par au moins quatre points du graphe, donc toute face du graphe est de degré au moins 4. En effet, il n'existe aucune canalisation reliant une maison à elle-même, donc le degré un n'est pas possible. Il n'existe pas deux canalisations reliant une même maison à un même fournisseur, le degré deux est encore impossible. Le degré trois suppose que, soit deux maisons, soit deux fournisseurs sont liés par une canalisation, ce qui est toujours impossible. Ceci donne la majoration :
En appliquant cette majoration à la formule d'Euler on obtient :
Or il existe neuf arêtes, trois par maison et six nœuds dont trois sont des maisons et trois des fournisseurs. La majoration aboutit alors dans le cas d'un graphe planaire à une contradiction : neuf est plus petit que huit. Cette contradiction montre que le graphe recherché ne peut être planaire[13].
Solutions avec d'autres géométries
Ruban de Möbius
.jpg.webp)
.jpg.webp)
L'impossibilité de résoudre l'énigme est une conséquence du théorème de Jordan. Une géométrie pour laquelle une solution existe doit donc admettre des courbes de Jordan qui ne divisent pas l'espace en deux composantes connexes par arcs. Comme le montre le paragraphe intitulé Topologie géométrique, la recherche d'une solution sur une sphère est vaine, une méthode rapide pour s'en convaincre est de remarquer que le théorème de Jordan est valide sur cette géométrie.
En revanche, le théorème ne s'applique pas si l'espace n'est pas orientable. Dans un espace non orientable, le côté droit de certaines courbes finit par devenir le côté gauche. Autrement dit, le concept de droite et de gauche n'a pas de sens sur un tel espace. Tel est le cas sur un ruban de Möbius[14]. La ligne à égale distance des deux bords possède cette propriété. Placer les trois maisons et les trois fournisseurs sur une telle ligne, à l'image de la figure de gauche, est judicieux[Note 5]. Les six premières canalisations n'ont alors pas coupé la géométrie en deux composantes connexes par arcs.
Pour comprendre ce qu'il advient une fois ces six premières canalisations posées, le plus simple est de construire un ruban de Möbius, de dessiner les différents nœuds et de couper effectivement le ruban. On obtient la figure en haut à droite (on n'a pas représenté la double torsion induite par le découpage dans la mesure où celle-ci ne change pas la résolution de l'énigme). Le ruban devient un unique nouveau ruban, deux fois plus long et deux fois moins large. Une des frontières du ruban contient maintenant deux séries des six nœuds à la suite l'une de l'autre.
Pour une raison de simplicité, il est plus simple de déformer le cylindre obtenu. On resserre la frontière ne contenant pas les nœuds jusqu'à ce que cette frontière soit réduite à un point, on ajoute alors ce point (on a vu précédemment que cela ne change rien à la résolution de l'énigme) pour obtenir un cône. Aplatir ce cône, ce qui ne change encore rien à l'existence ou l'absence de solution, donne la figure en bas à droite[Note 6]. Il devient aisé de trouver comment placer les trois dernières canalisations. La solution en bas à droite est celle qui est illustrée à gauche, une fois réalisées les transformations inverses[15].
Tore
.jpg.webp)
.jpg.webp)
Le ruban de Möbius est un exemple de surface qui ne satisfait pas le théorème de Jordan car il n'est pas orientable. D'autres surfaces sont orientables et ne satisfont néanmoins pas le théorème. C'est le cas du tore. Il existe cette fois, non pas un, mais deux types de courbes de Jordan dont le complémentaire est connexe par arcs. Pour cette raison, il est possible de résoudre l'énigme[16], même avec quatre maisons et quatre fournisseurs. Le fait de considérer une géométrie contenant un trou, comme le tore autorise la représentation de graphe non planaire. Tout graphe se représente sur une surface ayant un nombre de trous, encore appelé genre de la surface[17], suffisamment élevé. Sur une telle surface, et à condition de s'y prendre convenablement, il existe deux courbes de Jordan qui ne créent pas de nouvelles faces, l'équation d'Euler s'écrit alors n - a + f = 0. S'il existe quatre maisons et quatre fournisseurs, le graphe est composée de huit nœuds et seize arêtes, ce qui implique l'existence de huit faces. Le nombre moyen d'arêtes par face est le double du nombre d'arêtes, on trouve donc comme valeur moyenne quatre. Comme c'est aussi le nombre minimal d'arêtes pour une face, la solution ne comporte que des faces à quatre arêtes.
La première courbe de Jordan est illustrée sur la figure en haut à gauche. Comme pour le ruban de Möbius, on obtient un cylindre, illustré à droite. Cette fois-ci, les nœuds ne se trouvent pas tous en haut mais une série est sur la frontière haute et une sur la frontière basse. La technique précédente, pour transformer le cylindre en disque reviendrait à identifier les différents nœuds en un unique point, ce qui n'est pas acceptable. En revanche, il est possible d'établir un lien entre le nœud M1 situé en bas (avec les notations précédentes M1 correspond à la première maison. Les maisons sont illustrées en bleu sur les figures) et le nœud F2 (qui désigne le deuxième fournisseur. Les fournisseurs sont illustrés en rouge sur les figures). Ce lien est illustré en vert sur la figure en haut à droite. On obtient alors une figure comparable à un disque. Ce disque, illustré en bas à droite, comporte dix-huit nœuds. Chaque nœud est représenté deux fois, à l'exception des nœuds M1 et F1 qui le sont trois fois. La zone supérieure est représentée en gris clair et celle inférieure en gris foncé. Sous cette forme de disque, trouver la bonne configuration est aisée[17].
On peut se demander si une solution existe pour cinq fournisseurs et cinq maisons. Le même calcul montre que le nombre moyen d'arêtes par face est égal à dix tiers, soit strictement inférieur à quatre. Or quatre est le minimum d'arêtes pour construire une face pour cette énigme. La recherche d'une solution est donc vaine.
Notes et références
.jpg.webp)
Notes
- Mathématiquement, l'assertion de Georges Perec n'est pas totalement exacte : si les trois énoncés sont élémentaires, et si la résolution de l'énigme des ponts de Königsberg est facile, celle de l'article l'est déjà moins et celle des quatre couleurs ne l'est plus du tout. De plus, sur un tore ou un ruban de Möbius, des surfaces de dimension deux, une solution existe.
- Cette version possède l'avantage d'interdire la solution illustrée droite. C'est une solution où la canalisation alimentant en gaz la maison 2 traverse la maison 3. En mathématique, elle n'est pas acceptable, car aucun lien ne relie le nœud de la maison 2 au nœud du fournisseur gaz. Sous la forme de l'énigme, elle ne l'est généralement pas non plus, même si certains sites populaires comme Trois maisons sur Pedagonet l'acceptent.
- Il existe deux manières de définir l'homotopie dans le cas de l'article. On peut appliquer le concept aux chemins, deux chemins sont homotopes si l'on peut continument déformer le premier pour le superposer au second. On peut aussi appliquer le concept au graphe, ce qui revient à pouvoir aussi déplacer continument les points du graphe. La convention choisie dans ce paragraphe est de n'appliquer l'homotopie qu'aux chemins. Sinon, il n'existe qu'un nombre fini de graphes homotopes.
- Cette formule est démontrée dans l'article Graphe planaire.
- Pour mieux modéliser la surface, il est judicieux de la réaliser à l'aide d'un papier transparent, type papier calque.
- Ces différentes transformations correspondent à ce que l'on appelle en mathématiques des homéomorphismes. On démontre rigoureusement qu'appliquer un homéomorphisme à un espace ne modifie pas la nature de la question.
Références
- Georges Perec, Je me souviens, (réédition de 1998) Souvenir no 292, (ISBN 2012354564)
- Citations traduites de (en) H. E. Dudeney, Amusements in mathematics, pb 251
- (en) M. Gardner, The Sixth Book of Mathematical Games from Scientific American, University of Chicago Press, 1984 (ISBN 978-022628250-3), p. 92-94
- On trouve cette anecdote dans T. Chomette, Graphes planaires.
- On trouve aussi cette anecdote dans des sites plus populaires : G. Villemin, Les trois maisons, par le site : Nombres – Curiosités, théorie et usages.
- Cette citation est extraite du site www.mathsaharry.com, énigme no 74 par Math au matou.
- La démonstration usuelle n'en fait pas usage (voir T. Chomette, Graphes planaires).
- C'est le mathématicien Bernard Bolzano qui se pose le premier la question : J. Sebestik, Logique et mathématique chez Bernard Bolzano, Vrin, 2002 (ISBN 978-271161067-9), p. 26.
- Cette démonstration s'inspire de (en) T. Nishizeki et M. S. Rahman, Planar Graph Drawing, World Scientific Publishing, 2004 (ISBN 978-981256033-9), p. 24..
- Le vocabulaire est défini dans T. Chomette, Graphes planaires, p. 1.
- Les détails de l'origine de cette question sont traités dans l'article : J. Mayer, « Le théorème des quatre couleurs : notice historique et aperçu technique », Cahiers du séminaire d'histoire des mathématiques, t. 3, 1982, p. 43-62.
- K. Kuratowski, « Sur le problème des courbes gauches en topologie », Fund. Math., vol. 15, 1930, p. 271-283.
- On trouve ce raisonnement dans T. Chomette, Graphes planaires, p. 7.
- (en) Richard K. Guy et Robert E. Woodrow, The Lighter Side of Mathematics : Proceedings of the Eugene Strens Memorial Conference on Recreational Mathematics and Its History, American Mathematical Society, (présentation en ligne), p. 292
- Les éléments pour résoudre cette énigme sur un ruban de Möbius sont donnés et la question est proposée sous forme d'exercice : M. Habib, Notes de cours algorithmique de graphes, Magistère informatique Cachan.
- Ce contournement est fréquent, même dans les sites populaires, comme celui du professeur de mathématiques L. Lafaye, Notions de graphes.
- (en) F. Harary A. Hill, On the number of crossings in the complete graph, Proc. Edimburgh Math. Soc., 13 (1963), p. 333-338
Voir aussi
Bibliographie
- T. Chomette, Graphes planaires, cultureMATH (lire en ligne [PDF])
- (en) J. L. Gross et T. W. Tucker, Topological Graph Theory, Courier Dover Publications, 2001 (ISBN 978-048641741-7).
- J.-C. Novelli, Quand les chemins ne se croisent pas, Les Graphes, de la théorie des jeux à l'intelligence artificielle (Bases pour terminale ES. Approfondissements), numéro hors série du journal Tangente, 2002 (ISBN 978-290973785-0).
Articles connexes
- Théorème de Kuratowski (caractérisant les graphes planaires)
- Théorème de Robertson-Seymour (une vaste généralisation du théorème précédent)
Liens externes
- (en) Eric W. Weisstein, « Utility Graph », sur MathWorld



.jpg.webp)
.jpg.webp)