Zero Moment Point
En robotique, le zero-tilting moment point (ZMP) est un point dynamique caractéristique utilisé en locomotion, et plus particulièrement pour la locomotion des robots humanoïdes. Il représente les points dans l'espace où le moment des forces de contact a deux de ses trois coordonnées nulles, ce qui correspond à une condition de non-basculement par rapport à un plan (par exemple le plan du sol).
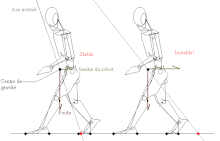
Histoire du concept
La notion de ZMP a été présentée pour la première fois par Miomir Vukobratović au Troisième Congrès de l'Union pour la Mécanique Théorique et Appliquée qui se tenait à Moscou en . Le terme « zero moment point » fit son apparition dans des travaux publiés pendant les années qui suivirent.
L'intérêt pour le ZMP prit son essor dans les années 1990, alors que les roboticiens l'appliquaient avec succès aux lois de contrôle pour la marche bipède. Le modèle fondamental qui permit ces développements est celui du pendule inversé : le haut du corps ayant une masse plus importante que les jambes, la marche consiste en première approximation au mouvement d'un pendule inversé, c'est-à-dire une masse reliée à une base mobile par une tige de masse nulle (le modèle "CART"). La masse en question représente le centre de gravité du robot, la tige sa jambe d'appui, et le point de base mobile n'est autre que le ZMP. Ce modèle fut appliqué avec succès aux robots HRP-2[1] et HRP-4C. Il se reconnaît par leur démarche particulière où le centre de gravité reste à hauteur constante.
Définition et calcul
Le ZMP est issu des équations de Newton-Euler (en) qui s'appliquent à tout système en mouvement dans l'espace. Celles-ci s'écrivent :
où est la masse totale du robot, le vecteur gravité, le centre de gravité du système, l'accélération du centre de gravité et le moment angulaire du système pris en un point arbitraire, tandis que et désignent respectivement la résultante et le moment du torseur des forces de contact appliquées au système. Le torseur gravito-inertiel, qui ne dépend que des accélérations du système, est défini quant à lui par :
Les équations de Newton-Euler s'écrivent alors de façon torsorielle : .
Le ZMP est un point de l'axe inertiel défini par
où désigne un vecteur normal (typiquement la normale au sol). Par rapport au moment en un autre point de référence, la partie gauche de cette équation devient :
Soit en utilisant la formule de développement du double produit vectoriel :
Supposons dans un premier temps que et sont dans le même plan de normale , de sorte que . On obtient alors, en injectant l'expression ci-dessus dans la définition du ZMP:
On utilise cette formule en pratique pour calculer le ZMP à partir de mesures par un capteur de force ou une centrale inertielle.
Lien avec le centre de pression
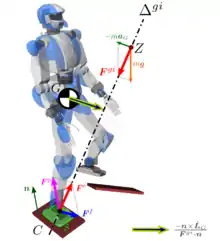
Le centre de pression est un point dynamique caractéristique d'un contact. Contrairement au ZMP, qui est défini en fonction de toutes les accélérations du robot, le COP est une grandeur locale définie à partir des forces exercées à la surface d'un contact. Toutefois, lorsqu'il n'y a qu'un seul contact, ou que le robot marche sur un sol horizontal, le COP et le ZMP coïncident[2].
La figure ci-contre représente le centre de gravité , le centre de pression du contact pied-droit ainsi qu'un ZMP . Les points et sont toujours alignés sur l'axe inertiel . Ce dernier ne passe pas nécessairement par le centre de gravité, à moins que le robot ne conserve son moment angulaire (), ce qui est une hypothèse de travail courante en locomotion[3].
Cas particulier du sol plat
Tant que le contact avec la surface ne rompt pas, le centre de pression réside nécessairement à l'intérieur de la surface de contact entre le robot et l'environnement. Lorsque les deux pieds du robot sont en contact avec la même surface (le sol), cette surface de sustentation est l'enveloppe convexe de tous les points d'appui, c'est-à-dire l'ensemble des points situés « entre les deux pieds ». Cette surface permet de définir les pressions et frottements, et donc un centre de pression associé (voir Centre de pression pour plus de détails). Le COP et ZMP coïncidant, nous obtenons le critère :
- Critère de non-basculement : pendant la marche sans basculement, le ZMP est situé à l'intérieur de la surface de sustentation, définie comme enveloppe convexe des points d'appui.
Ce critère est le plus fréquemment utilisé pour la marche des robots humanoïdes sur sol plat[1] - [4].
Notes et références
- S. Kajita, F. Kanehiro, K. Kaneko et K. Fujiwara, « Biped walking pattern generation by using preview control of zero-moment point », IEEE International Conference on Robotics and Automation, 2003. Proceedings. ICRA '03, vol. 2, , p. 1620–1626 vol.2 (DOI 10.1109/ROBOT.2003.1241826, lire en ligne, consulté le )
- P. Sardain et G. Bessonnet, « Forces acting on a biped robot. Center of pressure-zero moment point », IEEE Transactions on Systems, Man, and Cybernetics - Part A: Systems and Humans, vol. 34, , p. 630–637 (ISSN 1083-4427, DOI 10.1109/TSMCA.2004.832811, lire en ligne, consulté le )
- S. Kajita et K. Tani, « Study of dynamic biped locomotion on rugged terrain-derivation and application of the linear inverted pendulum mode », , 1991 IEEE International Conference on Robotics and Automation, 1991. Proceedings, , p. 1405–1411 vol.2 (DOI 10.1109/ROBOT.1991.131811, lire en ligne, consulté le )
- P. B. Wieber, « Trajectory Free Linear Model Predictive Control for Stable Walking in the Presence of Strong Perturbations », 2006 6th IEEE-RAS International Conference on Humanoid Robots, , p. 137–142 (DOI 10.1109/ICHR.2006.321375, lire en ligne, consulté le )
Voir aussi
Les robots humanoïdes suivants utilisent des lois de contrôle basées sur le ZMP :























