Union-find

Dans une telle forêt, le représentant de chaque classe est la racine de l'arbre correspondant. Find se contente de suivre les liens vers les nœuds pères jusqu'à atteindre la racine. Union réunit deux arbres en attachant la racine de l'un à la racine de l'autre. Une manière d'écrire ces opérations est la suivante :

 fonction MakeSet(x)
     x.parent := null
 fonction Find(x)
     si x.parent == null
        retourner x
     retourner Find(x.parent)
 fonction Union(x, y)
     xRacine := Find(x)
     yRacine := Find(y)
     si xRacine ${\displaystyle \neq }$ yRacine
            xRacine.parent := yRacine

Sous cette forme naïve, cette approche n'est pas meilleure que celle des listes chaînées, car les arbres créés peuvent être très déséquilibrés. Mais elle peut être améliorée de deux façons.

La première consiste à toujours attacher l'arbre le plus petit à la racine de l'arbre le plus grand, plutôt que l'inverse. Pour évaluer quel arbre est le plus grand, on utilise une heuristique appelée le rang[2] : les arbres contenant un élément sont de rang zéro, et lorsque deux arbres de même rang sont réunis, le résultat a un rang plus grand d'une unité. Avec cette seule amélioration, la complexité amortie des opérations MakeSet, Union et Find devient ${\displaystyle O(\log n)}$ au pire cas et ${\displaystyle O(1)}$ au meilleur cas. Voici les nouveaux codes de MakeSet et Union :

 fonction MakeSet(x)
     x.parent := x
     x.rang   := 0
 fonction Union(x, y)
     xRacine := Find(x)
     yRacine := Find(y)
     si xRacine ${\displaystyle \neq }$ yRacine
           si xRacine.rang < yRacine.rang
                 xRacine.parent := yRacine
           sinon
                 yRacine.parent := xRacine
                 si xRacine.rang == yRacine.rang
                         xRacine.rang := xRacine.rang + 1

La seconde amélioration, appelée compression de chemin, consiste à profiter de chaque Find pour aplatir la structure d'arbre ; en effet, chaque nœud rencontré sur le chemin menant à la racine peut être directement relié à celle-ci ; car tous ces nœuds ont le même ancêtre. Pour réaliser cela, on fait un parcours vers la racine, afin de la déterminer, puis un autre parcours pour faire de cette racine la mère de tous les nœuds rencontrés en chemin. L'arbre résultant ainsi aplati améliore les performances des futures recherches d'ancêtre, mais profite aussi aux autres nœuds pointant vers ceux-ci, que ce soit directement ou indirectement. Voici l'opération Find améliorée :

 fonction Find(x)
     si x.parent ${\displaystyle \neq }$ x
        x.parent := Find(x.parent)
     retourner x.parent

Ces deux améliorations (fusion optimisée des racines et compression de chemin) sont complémentaires. Ensemble, elles permettent d'atteindre une complexité amortie en temps ${\displaystyle O(\alpha (n))}$, où ${\displaystyle \alpha (n)}$ est la réciproque de la fonction ${\displaystyle f(n)=A(n,n)}$ et ${\displaystyle A}$ la fonction d'Ackermann dont la croissance est extrêmement rapide[3]. L'entier ${\displaystyle \alpha (n)}$ vaut moins de 5 pour toute valeur ${\displaystyle n}$ en pratique[4]. En conséquence, la complexité amortie par opération est de fait une constante.

Il n'est pas possible d'obtenir un meilleur résultat : Fredman et Saks ont montré en 1989 que ${\displaystyle \Omega (\alpha (n))}$ mots en moyenne doivent être lus par opération sur toute structure de données pour le problème des classes disjointes. Dasgupta et al., dans leur livre d'algorithmique, présente une analyse de complexité amortie en utilisant le logarithme itéré[5].

Exemple de forêts obtenues après union(a, b), union(c, d), union(a, c), find(d), union(b, e)[6].

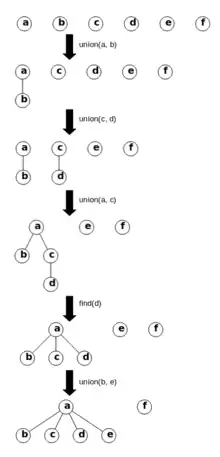
La figure à droite montre un exemple d'utilisation d'une structure de données union-find avec 6 éléments a, b, c, d, e, f. Au début, la forêt contient 6 arbres-racines : elle représente la relation d'équivalence où chaque élément est seul dans sa classe d'équivalence. L'opération union(a, b) connecte (par exemple), le nœud b à la racine a. L'opération union(c, d) connecte (par exemple), le noeud c à la racine d. L'opération union(a, c) connecte (par exemple) le nœud c au nœud a. L'opération find(d) retourne la racine a, mais au passage, il connecte d directement à la racine a (compression de chemins). L'opération union(b, e) commence par chercher les racines respectives a et e. Comme le rang de a est 1 et celui de e est 0, on connecte donc l'arbre e à l'arbre a.

• La pile spaghetti, nom donné au type d’arbres mis en œuvre dans la structure union-find.
• L’union de deux ensembles mathématiques.
• La partition d’un ensemble mathématique en sous-ensembles disjoints.

• Implémentation de union-find, graphique et en ligne

• Zvi Galil et Giuseppe F. Italiano, « Data structures and algorithms for disjoint set union problems », ACM Digital Library, septembre 1991 (consulté le 27 octobre 2007), Volume 23, Issue 3, pages 319-344
• J. A. Spirko and A. P. Hickman, « Molecular-dynamics simulations of collisions of Ne with La@C₈₂ », mai 1998 (consulté le 27 octobre 2007), Phys. Rev. A 57, 3674–3682
• Arthur Charguéraud et François Pottier:, « Verifying the Correctness and Amortized Complexity of a Union-Find Implementation in Separation Logic with Time Credits », J. Autom. Reasoning, vol. 62, n^o 3,‎ 2019, : 331-365 (lire en ligne)