Algorithme de Kruskal
En informatique, l'algorithme de Kruskal est un algorithme de recherche d'arbre recouvrant de poids minimum (ARPM) ou arbre couvrant minimum (ACM) dans un graphe connexe non-orienté et pondéré. Il a été conçu en 1956 par Joseph Kruskal.
Description du problème
On considère un graphe connexe non-orienté et pondéré : chaque arête possède un poids qui est un nombre qui représente le coût de cette arête. Dans un tel graphe, un arbre couvrant est un sous-graphe connexe sans cycle qui contient tous les sommets du graphe. Le poids d'un tel arbre est la somme des poids des arêtes qui le compose. Un arbre couvrant minimum est un arbre couvrant dont le poids est inférieur ou égal à celui de tous les autres arbres couvrants du graphe. L'objectif de l'algorithme de Kruskal est de calculer un tel arbre couvrant minimum.
Ce problème a de nombreuses applications, par exemple simplifier un câblage ou supprimer les liaisons maritimes les moins rentables en préservant l'accessibilité aux différents ports.
Principe de l'algorithme
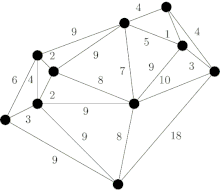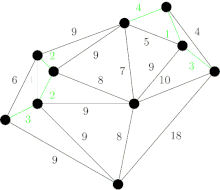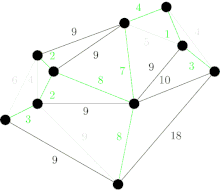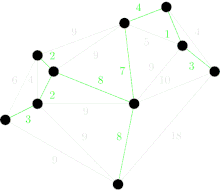
L'algorithme construit un arbre couvrant minimum en sélectionnant des arêtes par poids croissant. Plus précisément, l'algorithme considère toutes les arêtes du graphe par poids croissant (en pratique, on trie d'abord les arêtes du graphe par poids croissant) et pour chacune d'elles, il la sélectionne si elle ne crée pas un cycle. Le tableau suivant donne un exemple d'exécution de l'algorithme de Kruskal.
| Image | Description |
|---|---|
 |
AD et CE sont les arêtes de poids les plus faibles, ici 5. AD est sélectionnée de manière arbitraire. |
 |
CE est l'arête suivante de poids le plus faible. Elle est sélectionnée car elle ne forme pas de cycle. |
 |
L'arête DF de poids 6 est ensuite choisie. |
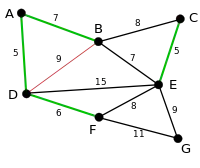 |
Les arêtes de poids faibles (7) suivantes sont AB et BE. AB est choisie de manière arbitraire. L'arête BD est dessinée en rouge car il existe un chemin (en vert) entre B et D. BD ne sera donc jamais sélectionnée. |
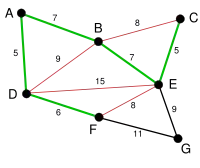 |
La prochaine arête considérée est BE de poids 7. BC ne sera jamais choisie car la choisir formerait le cycle BCE. De même DE formerait le cycle DEBA et FE formerait le cycle FEBAD. |
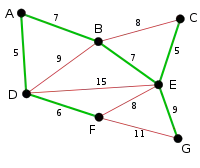 |
Finalement, l'arête EG de poids 9 est choisie et un arbre couvrant minimum est trouvé (en vert). |
On remarque que lors du déroulement de l'algorithme, les arêtes sélectionnées ne forment pas nécessairement un graphe connexe. Mais à la fin, les arêtes sélectionnées (en vert) forment un graphe connexe.
Algorithme
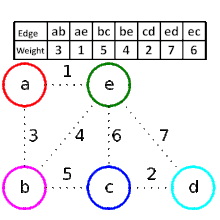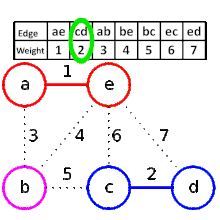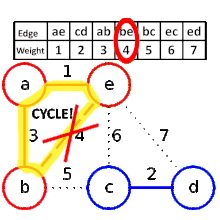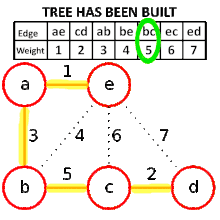
Pseudo-code
Kruskal(G) : 1 A := ø 2 pour chaque sommet v de G : 3 créerEnsemble(v) 4 trier les arêtes de G par poids croissant 5 pour chaque arête (u, v) de G prise par poids croissant : 6 si find(u) ≠ find(v) : 7 ajouter l'arête (u, v) à l'ensemble A 8 union(u, v) 9 renvoyer A
Les fonctions créerEnsemble, find et union sont les trois opérations d'une structure de données Union-Find – qui, respectivement, ajoute une classe singleton à la structure, renvoie un représentant de la classe d'un élément et fusionne deux classes d'équivalence.
Une amélioration possible est d'utiliser un tas à la place d'un tri afin de diminuer la complexité.
Preuve de correction
La preuve se compose de deux parties. Premièrement, il est prouvé que l'algorithme produit un arbre couvrant. Deuxièmement, il est prouvé que l'arbre couvrant construit est d'un poids minimal.
Arbre couvrant
Soit un graphe connexe pondéré et soit le sous-graphe de produit par l'algorithme. ne peut pas avoir de cycle, car par définition une arête n'est pas ajoutée si elle aboutit à un cycle. ne peut pas ne pas être connexe, car la première arête rencontrée qui joint deux composants de aurait été ajoutée par l'algorithme. Ainsi, est un arbre couvrant de .
Minimalité
Nous montrons que la proposition suivante 'P' est vraie par récurrence : Si F est l'ensemble des arêtes choisie à n'importe quel stade de l'algorithme, alors il y a un arbre couvrant minimum qui contient «F» ainsi qu'aucune des arêtes qui ont été rejetées par l'algorithme.
- Clairement 'P' est vrai au début, quand F est vide: n'importe quel arbre couvrant minimum fera l'affaire, et il en existe un car un graphe connexe pondéré a toujours un arbre couvrant minimum .
- Supposons maintenant que 'P' soit vrai pour un ensemble d'arêtes non final F et que T soit un arbre couvrant minimum contenant F .
- Si l'arête suivante choisie a est également dans T , alors 'P' est vrai pour F + a .
- Sinon, si a n'est pas dans T alors T + a a un cycle C. Ce cycle contient des arêtes qui n'appartiennent pas à F , puisque a ne forme pas un cycle lorsqu'il est ajouté à F mais le fait dans T . Soit b une arête qui est dans C mais pas dans F + a . Notons que b appartient également à T et que 'P' n'a pas été pris en compte par l'algorithme. b doit donc avoir un poids au moins aussi grand que a . Puis T - b + a est un arbre, et il a le même poids ou moins que T . Donc T - b + a est un arbre couvrant minimum contenant F + a et encore une fois 'P' tient.
- Par conséquent, selon le principe de récurrence, 'P' vaut quand F est devenu un arbre couvrant, ce qui n'est possible que si F est un arbre couvrant minimum lui-même.
Complexité
De manière générale, la complexité de l'algorithme est Θ(E log E) + Θ(E(|find| + |union|)), avec E le nombre d'arêtes du graphe G, et |find| et |union| les complexités respectives des opérations de recherche et d'union de notre structure Union-Find.
Une représentation naïve, utilisant des tableaux, aura donc une complexité en temps Θ(E x V), dominée par |find| = Θ(V) avec V le nombre de sommets du graphe G. Cette complexité se trouve fortement améliorée par une implémentation utilisant des arbres, passant à Θ(E log V). En compressant les chemins, on peut même atteindre une complexité amortie en temps Θ(E log* V).
Référence
Voir aussi
Bibliographie
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest et Clifford Stein, Introduction à l'algorithmique, Dunod, [détail de l’édition]

