Triangulation de graphe
La triangulation de graphe est un problème d'algorithmique et de théorie des graphes.
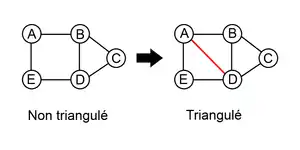 |
| Triangulation d'un graphe |
Définition
Notion
On travaille sur un graphe non orienté. Un graphe est triangulé si tout cycle de longueur supérieure à 3 admet une corde. On dit aussi qu'il est cordal.
Problème algorithmique
La triangulation d'un graphe non triangulé consiste à le rendre triangulé. La triangulation d'un graphe n'est pas unique et la recherche de la triangulation optimale (au sens du nombre d'arêtes ajoutées minimum) est un problème NP-Complet.
Algorithme
soit G un graphe non orienté
tantque il reste des sommets non marqués
sommet <- Choisir un Sommet
Relier deux à deux les voisins de sommet
Marquer(sommet)
Amélioration et Heuristique
L'algorithme ci-dessus est extrêmement simpliste. Il consiste à parcourir tous les sommets, de relier deux à deux les voisins du sommet, puis de le "supprimer" du graphe. Ceci pour tous les sommets. Complexité en sans compter le temps du choix du sommet. Cet algorithme ne trouve en rien une triangulation optimale (au sens du nombre d'arêtes ajoutées). Il permet juste de trouver une triangulation du graphe.
Choix de l'heuristique
On peut constater que l'efficacité de l'algorithme dépend de la manière de prendre les sommets. On peut donc naturellement faire intervenir différentes heuristiques pour améliorer grandement le résultat.
Heuristique avec score
Le score est calculé en fonction du nombre de voisins d'un sommet et du nombre de ses voisins reliés deux à deux. On essaye donc à chaque fois de prendre le sommet où le nombre d'arêtes à rajouter est le plus faible.
Avec deg égal au degré du sommet et nombreVoisinRelie le nombre de voisins reliés deux à deux du sommet en question.
Heuristique spécialisée
Bien que l'heuristique avec score se révèle efficace, il est souvent nécessaire de développer ses propres heuristiques en fonction du graphe. Par exemple en prenant en compte ses particularités symétriques.
Tester si un graphe est triangulé
L'algorithme le plus utilisé pour vérifier si un graphe est triangulé est un parcours en largeur lexicographique (dit Lex-BFS). Cet algorithme commence par numéroter chacun des sommets selon l'ordre défini dans l'algorithme qui est linéaire, .
Algorithme
Entrée Un graphe orienté Sortie La numérotation lambda des sommets de G Pour sommet étiquette(x)=0 FinPour Pour i=n jusqu'à 1 Choisir un sommet non numéroté d'étiquette lexicographique maximum Pour voisin non numéroté y de x Ajouter i à étiquette(y) FinPour FinPour
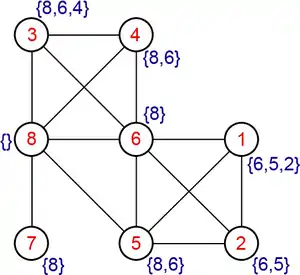 |
| LexBfs sur un graphe |






