Triangle d'or (géométrie)

Un triangle d'or (aigu) ou triangle sublime[1] est un triangle isocèle dans lequel le rapport de la longueur du côté double à la longueur du côté-base est le nombre d'or $\varphi$ :

{a \over b}=\varphi ={{1+{\sqrt {5}}} \over 2}\approx 1,618~034

(voir 1^ère figure).

Fig. 1 - Triangle d'or. Rapport a/b = nombre d'or φ. Angle au sommet :

\theta

= 36°. Angles de base : 72° chacun.

Certains auteurs[2] nomment également « triangles d'or » les triangles où ce rapport vaut ${1 \over \varphi }$ (voir § "Tableau récapitulatif" pour les différentes appellations).

Fig. 2 - Triangle d'or ABC découpé en un triangle d'or BXC et un gnomon d'or AXC.

Angles du triangle d'or

Dans la 2^e figure, BXC est un triangle d'or puisque le rapport de la longueur du côté BC à la longueur du côté BX est le nombre d'or $\varphi$ :

L'angle BCX au sommet C a pour mesure[3] :

\theta =2\arcsin {\bigl (}{\tfrac {b}{2a}}{\bigr )}=2\arcsin {\bigl (}{\tfrac {1}{2\varphi }}{\bigr )}=2\arcsin {\Bigl (}{\tfrac {{\sqrt {5}}-1}{4}}{\Bigr )}={\pi  \over 5}~rad=36^{\circ }.

Comme la somme des mesures des angles du triangle BXC fait $\pi ~rad$ , les angles de base CBX et CXB valent chacun :

\beta ={{\pi -{\pi  \over 5}} \over 2}={2\pi  \over 5}~rad=72^{\circ }

[1] (ou encore

\beta =\arccos {\Bigl (}{\tfrac {{\sqrt {5}}-1}{4}}{\Bigr )}={2\pi  \over 5}~rad=72^{\circ }

Le triangle d'or est un triangle aigu puisque tous ses angles sont inférieurs à l'angle droit.
Le triangle d'or est le seul triangle dont les mesures des angles sont dans des rapports 2, 2, 1 (72°, 72°, 36°)[4].

Occurrences

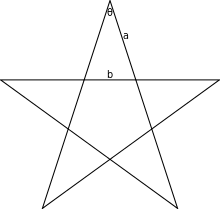
Pentagramme régulier : chaque branche est un triangle d'or.

Les branches du pentagramme régulier sont des triangles d'or (voir 3ème figure).
Dans le décagone régulier, lorsque l'on relie les sommets adjacents au centre, on obtient des triangles d'or[1].
Les pavages de Penrose font intervenir des triangles d'or.

Gnomon d'or

Un gnomon d'or ou triangle d'argent ou, pour certains auteurs, triangle d'or obtus[2] est un triangle isocèle obtus dans lequel le rapport de la longueur du côté double à la longueur du côté-base est l'inverse ${1 \over \varphi }$ du nombre d'or :

{a' \over b'}={1 \over \varphi }={{{\sqrt {5}}-1} \over 2}\approx 0,618~034.

Angles du gnomon d'or

Dans la 2^e figure, les longueurs AX et CX valant $a'=a=\varphi ~$ et la longueur AC valant $b'=\varphi ^{2}$ , AXC est un gnomon d'or[5].

L'angle AXC au sommet X a pour mesure :

\theta '=2\arcsin {\Bigl (}{\tfrac {b'}{2a'}}{\Bigr )}=2\arcsin {\Bigl (}{\tfrac {\varphi ^{2}}{2\varphi }}{\Bigr )}=2\arcsin {\Bigl (}{\varphi  \over 2}{\Bigr )}=2\arcsin {\Bigl (}{\tfrac {1+{\sqrt {5}}}{4}}{\Bigr )}={3\pi  \over 5}~rad=108^{\circ }

(ou encore

\theta '=\arccos {\Bigl (}{{1-{\sqrt {5}}} \over 4}{\Bigr )}={3\pi  \over 5}~rad=108^{\circ }

Comme la somme des mesures des angles du triangle AXC fait $\pi ~rad$ , les angles de base CAX et ACX valent chacun :

\beta '=\theta ={\pi -{3\pi  \over 5} \over 2}={\pi  \over 5}~rad=36^{\circ }

(ou encore

\beta '=\theta =\arccos {\Bigl (}{{1+{\sqrt {5}}} \over 4}{\Bigr )}={\pi  \over 5}~rad=36^{\circ }

Le gnomon d'or est un triangle obtus puisqu'il possède un angle obtus et deux angles aigus.
Le gnomon d'or est le seul triangle dont les mesures des angles sont dans des rapports 1, 1, 3 (36°, 36°, 108°).

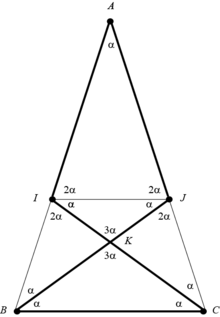
Construction en cure-dents ou à l'aide d'un pentagone articulé

Si on dispose cinq cure-dents identiques de sorte que, comme dans la figure ci-contre, $A, I, B$ soient alignés ainsi que $A, J, C$ , l'angle en $A$ vaut $\alpha =\pi /5$ et on obtient trois triangle d'or $ABC$ , $BCJ$ , $CBI$ , et quatre triangles d'argent $JAB$ , $IAC$ , $KBC$ , $KIJ$ . Cette construction peut aussi être obtenue par un pentagone articulé à barres de même longueur $AICBJ$ .

Tableau récapitulatif

Définitions de cet article	Définitions alternatives	$a \over b$	Angle au sommet	Angles égaux de base
Triangle d'or Triangle sublime	Triangle d'or aigu	$\varphi$	36°	72°
Gnomon d'or Triangle d'argent	Triangle d'or obtus	$1 \over \varphi$	108°	36°

Triangle (rouge) et gnomon (bleu) d'or découpés en un triangle (3 couleurs) et un gnomon (2 couleurs) d'or.

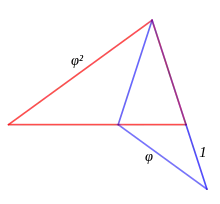
Triangle d'or et gnomon d'or associés

Découpages

La figure ci-contre montre que :

En coupant un de ses angles de base en 2 angles égaux, on peut découper un triangle d'or en un triangle d'or et un gnomon d'or.
En coupant son angle au sommet en 2 angles du simple au double, on peut découper un gnomon d'or en un gnomon d'or et un triangle d'or.

Pavages

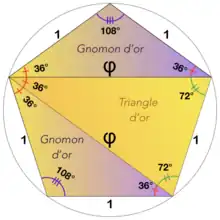
Deux gnomons d'or et un triangle d'or pavant un pentagone régulier.

On peut paver un pentagone régulier avec deux gnomons d'or et un triangle d'or[6] (voir figure ci-contre).
Ces triangles isocèles peuvent être utilisés pour produire les pavages de Penrose.

Spirale logarithmique

Triangles d'or inscrits dans une spirale logarithmique.

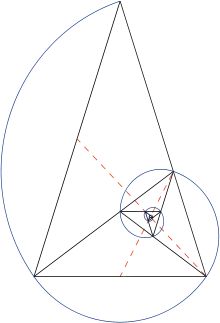
Le triangle d'or peut être utilisé pour placer certains points d'une spirale logarithmique. En procédant à la bissection d'un angle à la base d'un triangle d'or, on obtient un nouveau point, qui à son tour forme un nouveau triangle d'or[7]. En répétant ce procédé, on obtient des points qui permettent de tracer à main levée une spirale logarithmique (voir dernière figure).

Notes et références

(en) Kimberly Elam, Geometry of Design : Studies in Proportion and Composition, New York, Princeton Architectural Press, 2001, 107 p. (ISBN 1-56898-249-6, lire en ligne)
Par exemple Jean-Claude Thiénard, Maryse Cheymol, Maryse Combrade et Louis-Marie Bonneval, Mathématiques seconde (lire en ligne), p. 100
(en) Eric W. Weisstein, « Golden Triangle », sur mathworld.wolfram.com (consulté le 23 décembre 2019)
(en) « Tilings Encyclopedia »
(en) Arthur Livio, Concepts and Images : Visual Mathematics, Boston, Birkhäuser Boston, 1992 (ISBN 0-8176-3620-X)
(en) Eric W. Weisstein, « Golden Gnomon », sur mathworld.wolfram.com (consulté le 26 décembre 2019)
(en) H. E. Huntley, The Divine Proportion : A Study In Mathematical Beauty, New York, Dover Publications Inc, 1970, 186 p. (ISBN 0-486-22254-3, lire en ligne)

Voir aussi

Crédits de traduction

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Golden triangle (mathematics) » (voir la liste des auteurs).

Liens externes

(en) Eric W. Weisstein, « Golden Triangle », sur MathWorld
(en) Eric W. Weisstein, « Golden Gnomon », sur MathWorld
(en) Triangles de Robinson sur l'encyclopédie des pavages de l'Université de Bielefeld.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.