Treillis de Tamari
En mathématiques discrètes, et notamment en combinatoire, un treillis de Tamari, introduit par le mathématicien Dov Tamari, est un ensemble partiellement ordonné dont les éléments sont les différentes façons de grouper une suite d'objets en paires par parenthésage ; par exemple, pour la suite abcd de quatre objets, il y a cinq groupements possibles, qui sont : ((ab)c)d, (ab)(cd), (a(bc))d, a((bc)d), et a(b(cd)).
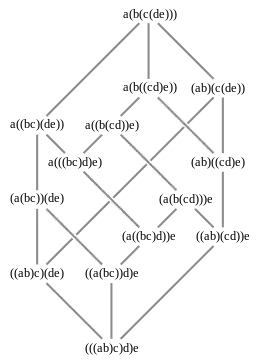
Description
Chaque groupement décrit une façon de combiner les objets par une opération binaire, ou aussi l'ordre dans lequel on évalue les opérations; dans un treillis de Tamari, les divers groupements sont ordonnés : un groupement précède un autre si le deuxième s'obtient à partir du premier par l'application de la règle d'associativité (xy)z → x(yz) qui repousse les parenthèses vers la droite. Par exemple, on obtient (a(bc))d → a((bc)d), et dans le treillis de Tamari, on a (a(bc))d ≤ a((bc)d).
Propriétés
Pour l'ordre ainsi introduit, deux éléments et possèdent toujours une borne inférieure , et une borne supérieure . Ainsi, le treillis de Tamari est bien un treillis au sens des ensembles ordonnés. Le plus grand élément est celui où les parenthésages se font le plus à gauche, et plus petit celui où les parenthésages sont le plus à droite. Le diagramme de Hasse de ce treillis est isomorphe au graphe d'un associaèdre. Le nombre d'éléments d'un treillis de Tamari pour une séquence de objets est le ième nombre de Catalan.
Définitions équivalentes
Le treillis de Tamari peut être décrit de plusieurs autres manières, toutes plus ou moins liées aux diverses interprétations des nombres de Catalan eux-mêmes :
- C'est l'ensemble des suites d'entiers tels que et, de plus, si , alors (Huang et Tamari 1972).
- C'est l'ensemble des arbres binaires, avec l'opération de rotation.
- C'est aussi l'ensemble des forêts ordonnées. Une forêt est inférieure à une autre si le ième nœud, dans un parcours préfixe de la première forêt a au moins autant de descendants que le ième nœud de la deuxième forêt (caractérisation citée dans : Knuth 2011, Section 7.2.1.6: Generating All Trees[1]).
- C'est l'ensemble des triangulations d'un polygone convexe à n sommets, ordonnées par l'opération flip qui consiste à enlever une arête de la triangulation, et de la remplacer, dans le quadrilatère apparaissant, par la diagonale opposée (ceci résulte de la dualité entre arbres binaires et triangulations).
- C'est aussi l'ensemble des chemins de Dyck de longueur , résultant du parcours des arbres binaires. L'ordre est induit par une rotation qui consiste à échanger un pas descendant avec le chemin de Dyck élémentaire (sans retour à 0) suivant.
Distance de rotation
La distance entre deux éléments d'un treillis de Tamari, vu comme un graphe, est la longueur de la plus courte chaîne qui relie ces éléments. Lorsque l'on considère les sommets du treillis comme des arbres binaires, cette distance est le nombre minimum de rotations qu'il faut faire pour passer du premier arbre au second. C'est pourquoi ce nombre est appelée distance de rotation. Le diamètre du treillis est la plus grande des distances de rotation dans le treillis. En 1988, Daniel Sleator, Robert Tarjan et William Thurston[2] montrent que le diamètre des treillis de Tamari n'est jamais plus grand que 2n-6 quand n est supérieur à 9. Ils montrent également que cette borne supérieure est atteinte quand n est suffisamment grand. Ils conjecturent alors que, dans cette phrase, « suffisamment grand » signifie « supérieur à 9 ». Cette conjecture a été résolue en 2012 par Lionel Pournin[3].
Notes et références
- Knuth donne, à la page 442 de son volume 4A, une table qui résume un ensemble de correspondances sur les éléments du treillis d'ordre 4. Ces correspondances font l'objet de nombreux exercices.
- Sleator, Tarjan et Thurston 1988.
- Pournin 2014.
Bibliographie
- Frédéric Chapoton, « Sur le nombre d'intervalles dans les treillis de Tamari », Séminaire Lotharingien de Combinatoire, vol. 55, , article no B55f (MR 2264942, arXiv math/0602368, lire en ligne).
- Edward Early, « Chain lengths in the Tamari lattice », Annals of Combinatorics, vol. 8, no 1, , p. 37–43 (DOI 10.1007/s00026-004-0203-9, MR 2061375).
- Haya Friedman et Dov Tamari, « Problèmes d'associativité: Une structure de treillis finis induite par une loi demi-associative », Journal of Combinatorial Theory, vol. 2, no 3, , p. 215–242 (DOI 10.1016/S0021-9800(67)80024-3, MR 0238984).
- Winfried Geyer, « On Tamari lattices », Discrete Mathematics, vol. 133, nos 1–3, , p. 99–122 (DOI 10.1016/0012-365X(94)90019-1, MR 1298967).
- Samuel Huang et Dov Tamari, « Problems of associativity: A simple proof for the lattice property of systems ordered by a semi-associative law », Journal of Combinatorial Theory, Series A, vol. 13, , p. 7–13 (DOI 10.1016/0097-3165(72)90003-9, MR 0306064).
- Donald E. Knuth, The Art of Computer Programming, vol. 4A : Combinatorial Algorithms, Part 1, Addison-Wesley, (ISBN 978-0-201-03804-0 et 0-201-03804-8, présentation en ligne)
- Lionel Pournin, « The diameter of associahedra », Advances in Mathematics, vol. 259, , p. 13–42 (DOI 10.1016/j.aim.2014.02.035, arXiv 1207.6296)
- Lionel Pournin, « A combinatorial method to find sharp lower bounds on flip distances », dans FPSAC'13 : 25th International Conference on Formal Power Series and Algebraic Combinatorics, DMTCS Proceedings, (lire en ligne), p. 1-11
- Daniel Sleator, Robert Tarjan et William Thurston, « Rotation distance, triangulations, and hyperbolic geometry », J. Am. Math. Soc., vol. 1, , p. 647–681
- Dov Tamari, « The algebra of bracketings and their enumeration », Nieuw Archief voor Wiskunde, Ser. 3, vol. 10, , p. 131–146 (MR 0146227).
- Folkert Müller-Hoissen, Jean Marcel Pallo et Jim Stasheff (éditeurs), Associahedra, Tamari lattices and related structures : Tamari memorial Festschrift, Birkhäuser/Springer Verlag, coll. « Progress in Mathematics » (no 229), .










