Titus Maximilien Huber
Titus Maximilien Huber (né le à Krościenko nad Dunajcem, village du Powiat de Nowy Targ, mort le à Cracovie) est un ingénieur et professeur polonais spécialisé dans la Résistance des matériaux.
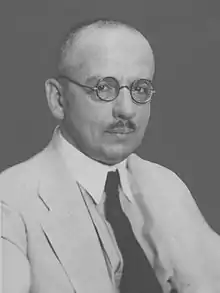
| Naissance |
Krościenko nad Dunajcem ( |
|---|---|
| Décès |
Cracovie ( |
| Nationalité |
|
| Résidence | Cracovie |
| Domaines | Résistance des matériaux |
|---|---|
| Institutions | Polytechnicum de Lvov |
| Renommé pour | Critère de plasticité de Huber-Mises |
Biographie
Il suivit de 1889 à 1894 une formation d'ingénieur au Polytechnicum de Lemberg. Après avoir effectué son service militaire, il obtint en 1898 une bourse qui lui permit d'étudier l’astronomie et les mathématiques à l'université Humboldt de Berlin[1]. Il est nommé l'année suivante assistant au Polytechnicum de Lemberg, et en devient professeur titulaire en 1908.
Au début de la première guerre mondiale, il est incarcéré par les Russes. En résidence à Kazan, il rencontre Timoshenko et Galerkine[1].
Avec la reconstitution d'un état polonais en 1919, il reprend ses activités comme professeur de mécanique dans ce qui est devenu le Polytechnicum de Lvov. À la fin des années 1920, on lui confia la chaire de mécanique de l'Université de Technologie de Varsovie. Avec Venceslas Olszak et Vitold Nowacki, il est considéré comme le fondateur de l'école polonaise de Mécanique. Après l'invasion de la Pologne, il s'efforce de maintenir malgré les interdictions un enseignement scientifique en polonais. À la libération, il est nommé par le gouvernement polonais professeur de Mécanique de l'université de Dantzig[1].
En 1949, il est nommé à la tête du département de mécanique de l'École des mines de Cracovie, poste qu'il occupe jusqu'à sa mort, survenue l'année suivante.
Œuvre
Théorie de l'écoulement plastique
Huber s'attacha à préciser la forme du critère de plasticité pour les métaux par des raisonnements sur l'énergie de distorsion[2]. Il arrive à la conclusion que le critère se confond avec le critère de la contrainte généralisée maximum énoncé par von Mises (et bien avant lui par Maxwell et Otto Mohr).
L'énergie (élastique) de distorsion est en effet exprimée par
où
- G est le module de cisaillement élastique
- sont les trois contraintes principales. Si l'on est en traction pure, deux de ces contraintes sont nulles (mettons ) et est une contrainte de traction. L'énergie de distorsion s'écrit alors :
Si la limite de résistance en traction du matériau est , l'énergie de distorsion critique est donc
Si l'on postule que la plastification du matériau se produit lorsque l'énergie de distorsion atteint cette valeur critique, alors :
Calcul rationnel des plaques en béton armé
Huber est le premier à utiliser le concept de raideur équivalente pour ramener l'estimation de la déformation des plaques raidies[3] - [4] - [5] au modèle continu de dalle orthotrope. Cette technique remédiait aux approches purement analytiques (Navier, Grashoff, Levy), impuissantes à décrire simultanément l'effet ponctuel des raidisseurs et à justifier la validité des solutions analytiques relatives à la flexion/torsion des plaques orthotropes. Elle sera poursuivie par le chercheur canadien Alexandre Hrennikoff[6].
Références
Voir également
Notes
- D'après (de) Karl-Eugen Kurrer, Geschichte des Baustatik, Berlin, Ernst & Sohn, , 539 p. (ISBN 3-433-01641-0, lire en ligne), p. 474
- M. Huber, « Le travail de distorsion spécifique comme mesure du taux de sollicitation d'un matériau », Czasopismo Techniczne, Lvóv, 3e série, no 22, , p. 80-81.
- M. T. Huber, « Die Grundlagen einer rationellen Berechnung der Kreuzweise beweherten Eisenbetonplatten », Zeitschrift des Oesterreichischen Ingenieur und Architekten-Vereines, no 66, , p. 557-564.
- M. T. Huber, « Die Theorie der Kreuzweise bewehrten Eisenbetonplatten nebst Anwendungen auf mehrere bautechnisch wichtige Aufgaben uiber rechteckige Platten », Bauingenieur, no 4, , p. 354-360 et 392-395.
- M. T. Huber, « Probleme der Statik Technisch Wichtiger Orthotroper Platten », Nakkadem Akadenji Nauk Technicznych, Varsovie, Poland, .
- A. Hrennikoff, « Solution of Problems of Elasticity by the Frame-Work Method », ASME J. Appl. Mech., no 8, , A619–A715
![{\displaystyle U={\frac {1}{12G}}[(\sigma _{1}-\sigma _{2})^{2}+(\sigma _{2}-\sigma _{3})^{2}+(\sigma _{3}-\sigma _{1})^{2}]}](https://img.franco.wiki/i/72a8b7c8347665768a695946d18dc36b24865bdc.svg)






