Théorie du premier gradient

Problème mécanique type.

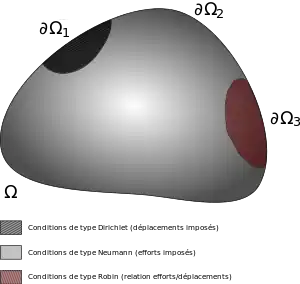
On considère ici un milieu continu occupant à chaque instant ${\displaystyle t}$ le domaine ${\displaystyle \Omega _{t}}$ de frontière ${\displaystyle \partial \Omega _{t}}$. Sur une partie de la frontière ${\displaystyle \partial _{1}\Omega _{t}}$, on a une condition de Dirichlet, c'est-à-dire de déplacement imposé. Sur une partie ${\displaystyle \partial _{2}\Omega _{t}}$ on a une condition de type Neumann, c'est-à-dire d'effort surfacique imposé ${\displaystyle {\underline {T}}}$. Le milieu est soumis à la densité d'effort volumique ${\displaystyle {\underline {f}}}$.

Les champs virtuels considérés sont les champs ${\displaystyle {\underline {v}}^{\star }}$ suffisamment réguliers, c'est-à-dire à énergie finie.

Pour appliquer le principe des puissances virtuelles, on a besoin de se donner une description pour ${\displaystyle {\mathcal {P}}_{i}^{\star }}$, la puissance des efforts intérieurs du système ${\displaystyle \Omega _{t}}$ considéré dans le champ de vitesse virtuel ${\displaystyle v^{\star }}$. Dans la théorie du premier gradient on fait l'hypothèse suivante concernant la puissance des efforts intérieurs :

1. Il existe une densité ${\displaystyle {p}_{i}^{\star }}$ de puissance des efforts intérieurs, telle que la puissance intérieure de tout sous-système ${\displaystyle \omega _{t}}$ ${\displaystyle {\mathcal {P}}_{i}^{\star }}$ soit l'intégrale de ${\displaystyle {p}_{i}^{\star }}$ sur domaine ${\displaystyle \omega _{t}}$.
2. La densité ${\displaystyle p_{i}^{\star }}$ est une fonction linéaire de ${\displaystyle v^{\star }}$ et de ses dérivées spatiales d'ordre 1.

Ces hypothèses ont pour conséquences d'une part que la puissance des efforts intérieur dans un milieu continu peut s'écrire à l'aide d'un opérateur tensoriel d'ordre 2 symétrique, noté ${\displaystyle {\underline {\underline {\sigma }}}}$ et appelé tenseur des contraintes de Cauchy, et d'autre part les équations locales usuelles d'équilibre des milieux continus à savoir :

On peut montrer que la partie liée aux dérivées d'ordre 0 de ${\displaystyle v^{\star }}$ est nulle (voir gradient d'ordre 0 ici). On recherche donc ${\displaystyle p_{i}^{\star }}$ sous la forme :

${\displaystyle p_{i}^{\star }=-{\underline {\underline {t}}}:{\underline {\underline {\nabla }}}~{\underline {v}}^{\star }}$

où ${\displaystyle {\underline {\underline {t}}}}$ est un tenseur d'ordre 2, et ${\displaystyle {\underline {\underline {\nabla }}}}$ est l'opérateur gradient tensoriel et ${\displaystyle$ :} désigne le produit doublement contracté.

On décide de décomposer ${\displaystyle {\underline {\underline {t}}}}$ et ${\displaystyle {\underline {\underline {\nabla }}}~{\underline {v}}^{\star }}$ en partie symétrique et antisymétrique comme suit :

On rappelle que le produit doublement contracté d'un tenseur symétrique avec un tenseur antisymétrique est nul.

On peut alors écrire ${\displaystyle p_{i}^{\star }=-{\underline {\underline {\sigma }}}:{\underline {\underline {D}}}-{\underline {\underline {\alpha }}}:{\underline {\underline {\Omega }}}}$

Soit ${\displaystyle {\underline {v}}^{\star }={\underline {v_{0}}}^{\star }+{\underline {\Omega _{0}}}^{\star }\wedge {\underline {x}}}$ un champ de vitesse rigidifiant (avec ${\displaystyle {\underline {v_{0}}}^{\star }}$ et ${\displaystyle {\underline {\Omega _{0}}}^{\star }}$ uniformes), on a alors : ${\displaystyle {\underline {\underline {D}}}={\underline {\underline {0}}}}$ et ${\displaystyle {\underline {\underline {\Omega }}}=\left({\begin{matrix}0&-{\Omega _{0}}_{3}&-{\Omega _{0}}_{2}\\{\Omega _{0}}_{3}&0&-{\Omega _{0}}_{1}\\{\Omega _{0}}_{2}&{\Omega _{0}}_{1}&0\end{matrix}}\right)}$

En utilisant la nullité de la puissance virtuelle des efforts intérieure pour un mouvement rigidifiant, on obtient la relation suivante :

${\displaystyle -{\underline {\underline {\Omega }}}:\int _{\omega _{t}}{\underline {\underline {\alpha }}}d\omega _{t}=0,\forall \Omega _{0}^{\star },\forall \omega _{t}\in \Omega _{t}}$

On a donc nécessairement ${\displaystyle {\underline {\underline {\alpha }}}={\underline {\underline {0}}}}$

On vient donc de montrer que suivant les hypothèses du premier gradient, la puissance des efforts intérieurs peut s'écrire :

${\displaystyle -\int _{\Omega _{t}}{\underline {\underline {\sigma }}}:{\underline {\underline {D}}}=-\int _{\Omega _{t}}{\underline {\underline {\sigma }}}:{\underline {\underline {\nabla }}}~{\underline {v}}^{\star }}$

Arrivé à ce stade, on peut écrire l'autre volet du PPV :

${\displaystyle {\mathcal {P}}_{i}^{\star }+{\mathcal {P}}_{e}^{\star }={\mathcal {P}}_{a}^{\star }}$

En utilisant les expressions naturelles pour les puissances des efforts extérieurs et la puissance d'accélération, et en appliquant le théorème de la divergence sur l'expression de la puissance des efforts intérieurs, on obtient :

Ce qui n'est autre que la formulation faible du système d'équation suivant : ${\displaystyle \left\{{\begin{aligned}{\underline {div}}~{\underline {\underline {\sigma }}}+{\underline {f}}-\rho {\underline {\gamma }}=0&{\mbox{ dans }}\Omega _{t}\\{\underline {\underline {\sigma }}}\cdot {\underline {n}}={\underline {T}}&{\mbox{ sur }}\partial \Omega _{t}\end{aligned}}\right.}$

Contribution d’une liaison à la puissance des efforts intérieurs.

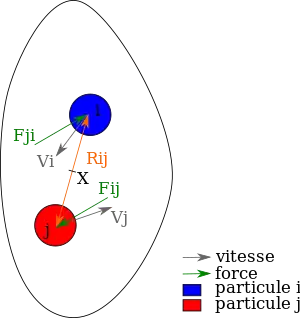
Pour cette approche, nous allons modéliser la contribution ${\displaystyle dP_{i}^{\star }}$ d’une liaison entre deux molécules à la puissance des efforts intérieurs. On considère une liaison entre deux molécules, i et j, centrée au point ${\displaystyle {\underline {x}}}$. On note ${\displaystyle {\underline {F_{ij}}}}$ l'effort de i sur j, et ${\displaystyle {\underline {v_{i}}}^{\star }}$ la vitesse virtuelle de la particule i. On pose ${\displaystyle {\underline {R_{ij}}}={\underline {x_{j}}}-{\underline {x_{i}}}}$

Le principe des actions réciproques permet d’écrire que ${\displaystyle {\underline {F_{ij}}}=-{\underline {F_{ji}}}}$

La puissance élémentaire est donnée par :

Or, comme on a choisi ici une échelle microscopique, il est raisonnable de relier les vitesses ${\displaystyle {\underline {v_{k}}}^{\star }}$ à la vitesse ${\displaystyle {\underline {v}}^{\star }({\underline {x}})}$ à l’aide d’un développement limité :

Ceci nous permet d’écrire que :

Cette expression permet d’écrire la participation à la puissance des efforts intérieurs d’une liaison ; or, en un point, il peut y avoir plusieurs molécules reliées. De plus on n'a aucune information a priori sur ${\displaystyle {\underline {F_{ij}}}}$ ce qui ne permet pas d’obtenir beaucoup d’information sur l’opérateur ${\displaystyle {\underline {\underline {t}}}}$.

Arrivé à ce stade, on retombe sur les raisonnements développés dans l’approche mathématique. L’approche physique ne sert qu’à donner une justification à l’existence de la densité de puissance des efforts intérieurs.

• Paul Germain, « La méthode des puissances virtuelles en mécanique des milieux continus », Journal de Mécanique, Paris, Gauthier-Villars, n^o 12,‎ 1973, p. 235–274
• A. Cemal Eringen, Microcontinuum field theories, New York, Springer Verlag, 1999, 348 p.
• R. D. Mindlin et N. N. Eshel, « On first gradient theories in linear elasticity », Int. J. Solids & Struct., vol. 4,‎ 1968, p. 109-124 (lire en ligne)