Théorème de Feuerbach
En mathématiques, le théorème de Feuerbach, du nom du mathématicien Karl Feuerbach, affirme que dans un triangle, le cercle d'Euler est tangent au cercle inscrit et aux trois cercles exinscrits. Les points de contact sont appelés points de Feuerbach du triangle[1].
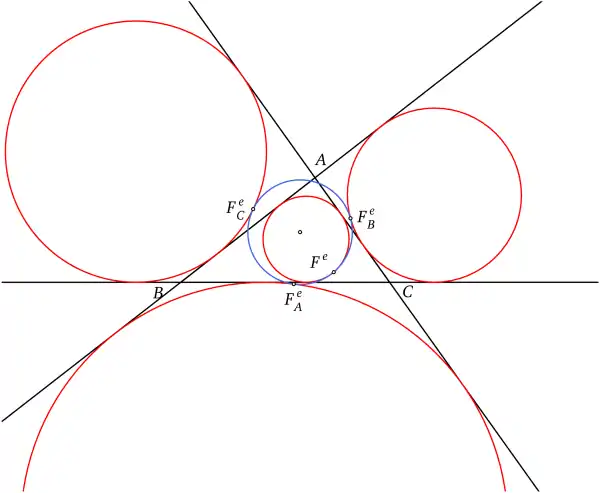
Points de Feuerbach
Les trois points de tangence des cercles exinscrits forment le triangle de Feuerbach du triangle ABC[2].
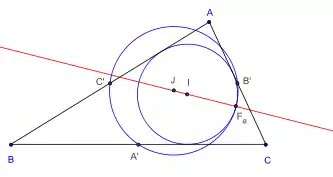
Le point de Feuerbach Fe, point de contact du cercle d'Euler et du cercle inscrit, est situé sur la droite des centres (IJ), avec I le centre du cercle inscrit et et J le centre du cercle d'Euler.
Soit S, le point de concours des droites . Alors les points J, I, S et le point de Feuerbach Fe sont alignés et en division harmonique[2].
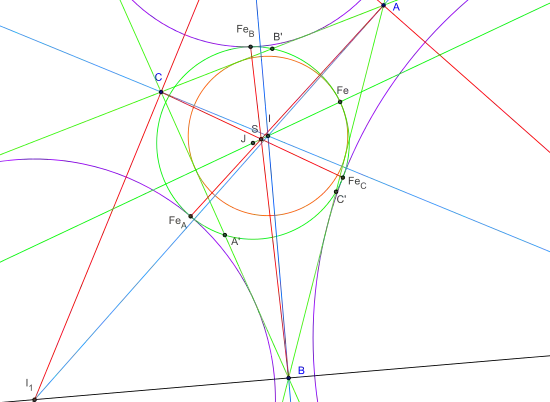
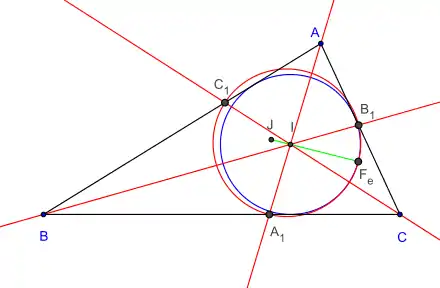
Le point de Feuerbach Fe appartient aussi au cercle circonscrit du triangle cévien du centre I du cercle inscrit, ce dernier étant tangent en Fe au cercle inscrit et au cercle d'Euler[3].
Six autres droites concourantes au point de Feuerbach
- Trois droites symétriques des côtés du triangle de contact

Soit O le centre du cercle circonscrit et iA, iB, iC les points de contact du triangle ABC avec son cercle inscrit.
Les trois droites symétriques de la droite (IO), par rapport aux côtés du triangle de contact iAiBiC, passent par le point de Feuerbach.
- Trois droites symétriques des côtés du triangle de Feuerbach
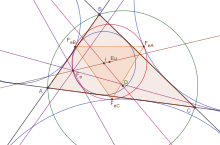
Les trois droites symétriques de la droite (IO), par rapport aux côtés du triangle de Feuerbach , passent par le point de Feuerbach.
Théorème de Feuerbach-Ayme dans un triangle rectangle

Soit ABC un triangle rectangle en A, H le pied de la hauteur de ABC sur (BC), OB et OC les centres des cercles inscrits dans les triangles AHB et AHC, et F0 le point de Feuerbach inscrit du triangle ABC ; alors les droites (C’OB) et (B’OC) sont orthogonales et se coupent au point de Feuerbach. Le cercle de diamètre [OBOC] passe par F0.
Remarque : outre le point de Feuerbach, le cercle de diamètre [OBOC] contient le pied H de la hauteur issue de A, le point de contact du cercle inscrit dans ABC avec le côté (BC) et les points d'intersection des bissectrices des angles aigus B et C avec la droite des centres (B’C’). Ces deux derniers points sont aussi situés sur les bissectrices en A des triangles AHB et AHC.
Liens externes
Bibliographie
- Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009 (ISBN 978-2-91-635208-4)
Notes et références
- (en) Brian Sherman, « Feuerbach’s Theorem », Australian Mathematics Education Journal (AMEJ), vol. 3, no 1, , p. 44-46
- (en) Eric W. Weisstein, « Feuerbach Triangle », sur MathWorld
- (en) Lev Emelyanov et Tatiana Emelyanova, « A Note on the Feuerbach Point », Forum Geometricorum, vol. 1, , p. 121–124 (ISSN 1534-1178, lire en ligne)


