Le théorème d'Ayme est un résultat de septembre 2011[1] concernant la géométrie du triangle. C'est un théorème de géométrie projective. Le théorème a été découvert et démontré par Jean-Louis Ayme, professeur de mathématiques retraité à Saint-Denis de La Réunion.
Sommaire
Hypothèses du théorème
Triangle
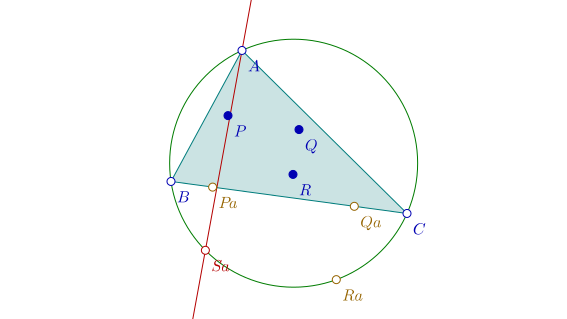
On considère un triangle ABC (en bleu) et son cercle circonscrit (en vert):
Trois points
On considère trois points P, Q et R du plan (ailleurs que sur les côtés de ABC):
Constructions de droites
Constructions basées sur le premier sommet
Avec P
La droite (AP) est la cévienne de P issue de A; elle coupe le côté opposé en un point Pa:
Avec Q
De même, la droite (AQ) coupe le côté opposé en Qa:
Avec R
Par contre, le point Ra est défini comme l'intersection de (AR) et du cercle circonscrit à ABC:
Cercle
Comme le triangle PaQaRa n'est pas aplati, il possède un cercle circonscrit (en rouge):
Point
L'intersection des deux cercles est formée de deux points; l'un d'eux est Ra.
Définition du point associé à A
L'autre point d'intersection des deux cercles est noté Sa ci-dessus.
Droite passant par A
On construit alors la droite (ASa):
Constructions basées sur le second sommet
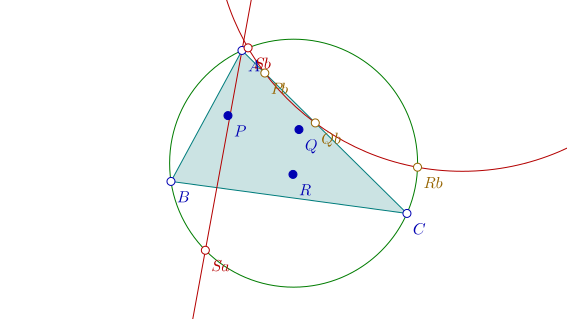
En répétant les constructions ci-dessus avec le point Q, on construit successivement
- le point Pb, intersection de (BP) et (AC);
- le point Qb, intersection de (BQ) et (AC);
- le point Rb, intersection de (BR) et du cercle circonscrit;
- le cercle circonscrit à PbQbRb (en rouge)
- L'intersection de ce cercle avec le cercle circonscrit à ABC: Le point Sb:
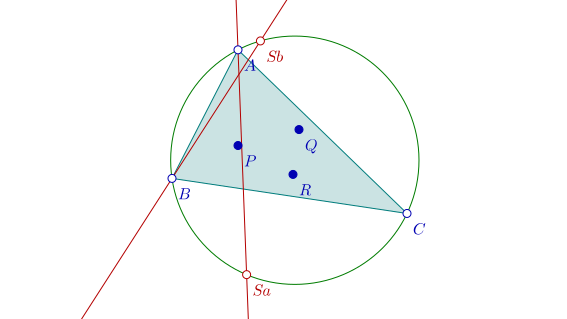
On joint alors le dernier point construit (Sb) au sommet B qui lui correspond:
Constructions basées sur le troisième sommet
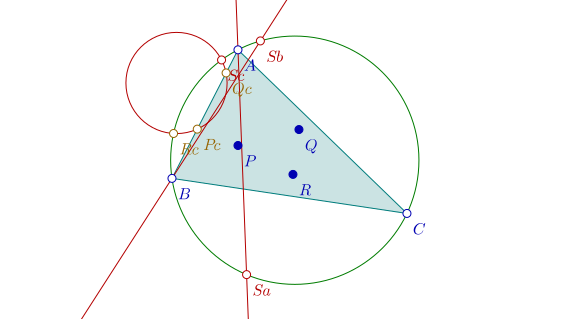
De même, on construit le point Sc correspondant au sommet C:
Énoncé du théorème
Théorème — Les trois droites (ASa), (BSb) et (CSc) sont concourantes.