Tempérament par division multiple

Plusieurs théoriciens ont conçu des tempéraments basés sur une division de l'octave en plus de douze intervalles élémentaires. Constatant que la division en douze intervalles égaux n'aboutit pas à la pureté des intervalles de quinte et de tierce, ils ont recherché si une division de l'octave en un nombre plus important d'intervalles, parmi lesquels on en choisirait sept (gamme diatonique), ne permettrait pas de se rapprocher de cette pureté idéale. De fait, plusieurs schémas de division ont ainsi été déterminés, qui permettent parfois d'améliorer aussi la qualité des autres notes. C'est d'ailleurs une évidence que plus l'intervalle élémentaire est petit, meilleure est l'approche de la pureté : de même qu'une règle graduée en millimètres donne une mesure plus précise qu'une règle graduée en centimètres.

Les principales divisions multiples[3] s'établissent selon le raisonnement suivant :

1. L'octave se divise en cinq tons et deux demi tons diatoniques ; la différence entre le ton et le demi-ton diatonique est le demi-ton chromatique.
2. Si les demi-tons valent exactement la moitié du ton (le demi-ton diatonique est égal au demi-ton chromatique), alors l'octave compte
   1. Six tons (gamme par tons)
   2. Douze demi-tons
   3. Dix-huit tiers de tons
   4. Vingt-quatre quarts de tons
   5. Etc.
3. Si le ton se subdivise en un nombre impair n d'unités, il existe deux formes du demi-ton, appelées l'une diatonique, l'autre chromatique. Dans les principaux systèmes de division multiple, les deux formes du demi-ton diffèrent d'une unité seulement : le plus grand vaut la moitié du ton + n/2, l'autre la moitié du ton – n/2. Si le demi-ton diatonique est le plus grand, alors l'octave vaut 5n + 2(n+1)/2 = 6n + 1. Si le demi-ton diatonique est le plus petit, l'octave vaut 5n + 2(n-1)/2 = 6n – 1. Les différents cas possibles sont alors :
   1. n = 3. Un des deux demi-tons vaut 2n/3, l'autre vaut n/3.
      1. 6n - 1 = 17 unités. Ne produit aucun intervalle approximant ceux de notre gamme diatonique. Par contre, cette division permet une approximation de la « tierce neutre » de certaines musiques orientales [4].
      2. 6n + 1 = 19 unités. En choisissant 12 de ces 19 unités, on obtient une excellente approximation du tempérament mésotonique au 1/3 de comma [5].
   2. n = 5. Un des deux demi-tons vaut 3n/5, l'autre vaut 2n/5.
      1. 6n - 1 = 29 unités. Résultat insatisfaisant. Ne semble pas décrite dans la littérature historique[6].
      2. 6n + 1 = 31 unités. C'est le système de l'archicembalo de Nicola Vicentino (1555)[7], qui donne une excellente approximation du tempérament mésotonique au 1/4 de comma[8].
   3. n = 7. Un des deux demi-tons vaut 4n/7, l'autre 3n/7.
      1. 6n - 1 = 41 unités. Produit d'excellentes quintes, mais les tierces sont insatisfaisantes[9].
      2. 6n + 1 = 43 unités. Cette division n'est pas satisfaisante musicalement, mais elle correspond à la division par Sauveur de l'octave en 43 mérides: c'est une division purement théorique, qui permettait à Sauveur de subdiviser ensuite chaque unité en 7 heptamérides pour arriver à un total de 301 dans l'octave, soit le logarithme décimal de 2 calculé avec trois décimales[10].
   4. n = 9. Un des deux demi-tons vaut 5n/9, l'autre 4n/9.
      1. 6n – 1 = 53 degrés. Système de Mercator ou de Holder[11], ou « système solfégique », où le ton est divisé en 9 commas. Excellente approximation du système pythagoricien.
      2. 6n + 1 = 55 degrés. Résultat intermédiaire entre le tempérament égal et le mésotonique au 1/4 de comma[12].
   5. Etc. Au dessus de n=9, les divisions deviennent si nombreuses qu'on parvient toujours à des approximations satisfaisantes de systèmes connus.

D'autres systèmes sont fondés sur des relations moins simples entre les demi-tons diatonique et chromatique. Nombre d'entre eux sont décrits dans les ouvrages anciens, mais rares sont ceux qui produisent des résultats satisfaisants.

Les tempéraments par division multiple n'ont de légitimité que s'ils apportent un véritable avantage en termes de musicalité. Ce sont en général plus des curiosités théoriques que des systèmes réellement mis en œuvre et ayant servi de support à de grandes œuvres. Ils ne peuvent être pratiqués simplement qu'avec la voix ou certains instruments à intonation variable (famille des violons, certains cuivres) ou par des instruments à sons fixes conçus pour eux et comportant des dispositifs « exotiques » tels que claviers glissants, doubles claviers, touches divisées etc. Leur peu de succès pratique tient aussi à la difficulté du jeu qui nécessite une formation spécifique de l'artiste : le jeu n'en vaut vraiment pas la chandelle.

Ces tempéraments considèrent que l’octave se divise en 5 tons et 2 demi-tons, ces derniers étant proches de la moitié d’un ton - disons qu’un ton sera compris entre 1,5 et 2,5 fois le demi-ton.

Si la proportion est de deux, on est ramené à l’octave divisée en 12 intervalles égaux, car 12 = 5 x 2 + 2 x 1 : c’est le tempérament égal habituel à douze intervalles égaux par octave.

En faisant varier cette proportion, on détermine, entre autres, les tempéraments à 19, 31, 43 et 53 intervalles par octave :

• 19 = 5 x 3 + 2 x 2 : la proportion est de 3/2 et le ton vaut 1,5 demi-tons ;
• 31 = 5 x 5 + 2 x 3 : la proportion est de 5/3 et le ton vaut 1,666… demi-tons ;
• 43 = 5 x 7 + 2 x 4 : la proportion est de 7/4 et le ton vaut 1,75 demi-tons ;
• 53 = 5 x 9 + 2 x 4 : la proportion est de 9/4 et le ton vaut 2,25 demi-tons.

Les nombres 19, 31 et 43 sont de la forme 12 x n + 7.

Bien évidemment, plus l’intervalle élémentaire divisant l’octave est petit, plus on a de chances d’obtenir un tempérament approchant au mieux la juste intonation. Cependant, on se heurte alors à la question, très concrète, de la « jouabilité » sur des instruments à commande manuelle (clavier, instruments à vent à clef). C’est cet aspect essentiel qui a empêché l’utilisation réelle de ces tempéraments, restés pour la plupart à l’état de construction théorique - une instrumentation électronique et/ou informatique peut au contraire les réaliser.

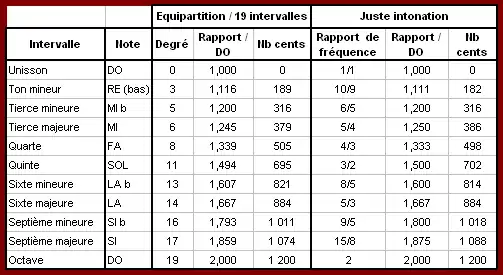
Un clavier réalisant le tempérament à 19 intervalles égaux

L’équipartition de l’octave en 19 intervalles présente la particularité d’approcher les intervalles diatoniques de la juste intonation - qui sont la référence sur le plan de l’audition et de la musique - généralement de plus près que le tempérament égal à 12 demi-tons (la gamme tempérée usuelle).

L’approximation est parfaite en ce qui concerne la tierce mineure et la sixte majeure. Elle est très bonne pour la tierce majeure et la sixte mineure. En revanche, la seconde majeure est en dessous de l'intonation juste et correspond au ton mineur (10/9) alors qu'on préfèrerait généralement un ton majeur (9/8).

L'harmonique 7 peut être différenciée, par exemple en jouant un intervalle Do - La# au lieu de Do - Si b pour exprimer le rapport de 7/4, cependant l'intervalle est nettement rétréci par rapport à l'intonation juste.

Dans le tableau ci-dessous, on n’a reporté que les degrés qui offrent une comparaison favorable.

Recommandé, mais non inventé[note 1], par Huyghens, ce tempérament peut être introduit simplement en considérant la proportion de 5 pour 3 entre le ton et le demi-ton.

Ce tempérament permet une excellente approximation de tous les intervalles classiques mais aussi de l'harmonique 7.

Il se trouve que la taille de la quinte et la proportion entre le ton et le demi-ton dans ce tempérament est pratiquement celle qui existe entre le ton et le demi-ton diatonique du tempérament mésotonique à ¼ de comma syntonique.

Dans ce dernier tempérament, en effet :

• la quinte tempérée vaut 5^1/4…
• le ton T, soit 2 quintes tempérées diminuées d’une octave vaut 5^1/2/2, environ 1,118034
• le demi-ton diatonique D, soit 3 octaves diminuées de 5 quintes tempérées vaut 2³/5^5/4, environ 1,069984
• on peut vérifier que T³ et D⁵ ont une valeur très proche, environ 1,4.

Si maintenant on considère le tempérament à 31 intervalles égaux, avec un ton qui en vaut 5 et un demi-ton diatonique qui en vaut 3, sa quinte en vaut 18 et elle égale donc 2^18/31.

On peut alors calculer l’intervalle enharmonique si${\displaystyle \sharp }$-do.

• dans la gamme pythagoricienne, il s’agit du comma ditonique.
• dans le tempérament de Huyghens, il vaut 7 octaves moins douze quintes :

2⁷ / (2^18/31)¹², ou encore, après les simplifications

2^1/31 c’est-à-dire l'intervalle élémentaire de Huyghens, qui joue donc à la fois le rôle d’intervalle élémentaire et de comma.

En complément de ce tempérament, le savant néerlandais préconisa un système de clavier glissant permettant de le concrétiser mais qui resta à l’état de curiosité théorique et mécanique. Adriaan Fokker a conçu et construit quelques claviers musicaux capable de jouer de la musique microtonale via un clavier général. Le mieux connu de ceux-ci est son clavier à 31 intervalles égaux bien tempéré, qui est installé au Muziekgebouw aan 't IJ. Il est familièrement appelé l'« orgue de Fokker ».

Ce tempérament présente d’intéressantes caractéristiques et la particularité de pouvoir être introduit par un raisonnement très différent : voir ci-dessous Tempérament de Sauveur

La construction de ce tempérament est directement issue de la gamme pythagoricienne, basée sur le fait que 12 quintes (rapport de fréquences 3/2) donnent quasiment 7 octaves (rapport de fréquences 2/1), soit (3/2)¹² ≈ (2/1)⁷, ou log(3/2)/log(2/1) ≈ 7/12. En effet, 7/12 est la réduite d’indice 4 du réel log(3/2)/log(2/1), donc une bonne approximation rationnelle de ce dernier. On peut donc construire des tempéraments de la même manière en utilisant les réduites suivantes de log(3/2)/log(2/1), à savoir 24/41, 31/53 ou 179/306[13] : le tempérament de Holder est ainsi basé sur l’approximation rationnelle 31/53, réduite d’indice 6.

Les calculs - détaillés dans cette dernière page - montrent qu’une octave s’y divise en une somme de 5 apotomes et 7 limmas. Si l’on tient compte de ce que, approximativement, l’apotome vaut 5 commas pythagoriciens et le limma en vaut 4, l’octave vaut environ 53 commas, soit 5 x 5 + 7 x 4.

Ceci amène naturellement à introduire l’intervalle élémentaire i, très proche du comma pythagoricien, tel que i⁵³ = 2 : le tempérament obtenu est régulier et approche au mieux les intervalles principaux de la gamme pythagoricienne, avec un ajustement possible au niveau des tierces, qui peuvent être rendues presque pures - car le comma syntonique est lui-même proche du pythagoricien.

L'intérêt théorique de cette division de l'octave a été mise en évidence dès l'Antiquité. Le théoricien chinois Ching Fang (78-37 av. J.-C.) a en effet découvert que 53 quintes pures sont très proches de 31 octaves (N.B. Le nombre 31 donne aussi une possibilité de division de l'octave - voir ci-dessus - mais ça n’est qu’une coïncidence numérique). Il a calculé l'écart entre ces intervalles qui peut être approché, avec 6 décimales, par la fraction 177147/176776. Bien plus tard, cette observation fut à nouveau faite par le mathématicien et théoricien de la musique Nicolaus Mercator (vers 1620-1687) qui en a donné la formule 3⁵³/2⁸⁴ : c'est le comma de Mercator. Le comma de Mercator est une valeur faible (environ 3,615 cents) qui, réparti sur les 53 quintes, devient négligeable dans la pratique. William Holder a par ailleurs remarqué que ce tempérament permet d'approcher de très près la tierce pure (avec un écart de 1,4 cent) - toutes ces caractéristiques en font donc un excellent tempérament, du point de vue théorique.

Joseph Sauveur, savant mathématicien et fondateur de l’acoustique bien que lui-même sourd, a imaginé un tempérament particulier à partir d’une propriété de la gamme naturelle diatonique et en bénéficiant d’un heureux hasard (?) algébrique.

Considérons les rapports de fréquences des huit notes « justes » d’une octave :

• DO 1
• RE 9/8
• MI 5/4
• FA 4/3
• SOL 3/2
• LA 5/3
• SI 15/8
• DO 2

il est facile de calculer les intervalles diatoniques correspondants :

• DO-RE 9/8
• RE-MI 10/9
• MI-FA 16/15
• FA-SOL 9/8
• SOL-LA 10/9
• LA-SI 9/8
• SI-DO 16/15

Donc une octave (O) égale 3 tons majeurs (T = 9/8) + 2 tons mineurs (t = 10/9) + 2 demi-tons diatoniques (D = 16/15) soit 5 tons et 2 demi-tons.

Sauveur définit :

• le « ton moyen » T_m tel que O = 5 x T_m + 2 x D ;
• le demi-ton mineur d = T_m - D (dit « mineur » car plus petit que le demi-ton diatonique D, qui est donc dit également « majeur ») ;
•  et enfin le comma de Sauveur c = D - d.

Les valeurs numériques (éventuellement approchées) sont les suivantes :

• ton majeur 9/8 = 1,125
• ton mineur 10/9 ≈ 1,1111…
• ton moyen (15²/2⁷)^1/5 ≈ 1,1194…
• 1/2 ton majeur 16/15 ≈ 1,0667…
• 1/2 ton mineur (15⁷/2²⁷)^1/5 ≈ 1,0495…
• comma (2⁴⁷/15¹²)^1/5 ≈ 1,0164…

On peut ensuite calculer combien il y a de commas de Sauveur dans une octave, et le calcul se fait à l’aide des logarithmes et montre qu’une octave vaut 42,6211… commas de Sauveur, valeur proche de 43. On retrouve, mais par un autre procédé, le tempérament à 43 intervalles égaux par octaves évoqué plus haut.

On notera que le comma de Sauveur n’est pas un comma stricto sensu mais une fraction de comma, en l’occurrence, le cinquième du comma constituant la différence entre :

• 12 quartes ;
• 12 tierces majeures augmentées d’une octave ;

ou, de manière équivalente, entre :

• 11 octaves ;
• 12 septièmes majeures.

Il y a une autre particularité mathématique : le logarithme à base 10 de 2 vaut 0,30103 or 301 (soit 1000 fois ce logarithme) égale 43 x 7. Ainsi, Sauveur peut introduire une unité d’intervalle musical, l’heptaméride tel que :

• le comma de Sauveur vaut 7 heptamérides,
• une octave vaut 301 heptamérides,

et, par approximation,

• un ton moyen = 7 commas = 49 heptamérides
• un 1/2 ton majeur = 4 commas = 28 heptamérides
• un 1/2 ton mineur = 3 commas = 21 heptamérides

(on peut vérifier, en traduisant en heptamérides, que l’octave vaut 5 tons moyens + 2 demi-tons majeurs).