TFNP
En théorie de la complexité computationnelle, la classe de complexité TFNP est la classe des problèmes fonctionnels totaux qui peuvent être résolus en temps polynomial non déterministe. C'est la classe des problèmes fonctionnels où on a la garantie d'avoir une réponse, et cette réponse peut être vérifiée en temps polynomial; ou encore, c'est le sous-ensemble de FNP où une solution est garantie. L'abréviation TFNP signifie "Total Function Nondeterministic Polynomial".
TFNP contient de nombreux problèmes naturels qui intéressent les informaticiens. Ces problèmes incluent la factorisation d'entiers, la recherche d'un équilibre de Nash et la recherche d'optima locaux. Il est largement supposé que TFNP contient des problèmes difficiles sur le plan informatique, et plusieurs de ces problèmes sont difficiles sous des hypothèses cryptographiques[1] - [2]. Cependant, il n'y a pas de résultats connus de difficulté inconditionnelle pour TFNP. On ne pense pas que TFNP ait des problèmes complets[3].
Définition
La classe TFNP est définie comme suit :
- Une relation binaire P(x, y) est dans TFNP si et seulement s'il existe un algorithme en temps polynomial déterministe qui peut déterminer si P(x, y) est vrai ou non, étant donné x et y, et pour chaque x, il existe un y dont la taille est bornée par un polynome en la taille de x tel que P(x, y) soit vérifié.
Sous-classes notables
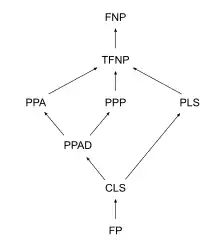
Les sous-classes de TFNP sont souvent définies par le théorème mathématique qui garantit l'existence d'une solution.
Une des sous-classes est PPA.
Notes et références
- Garg, Pandey, and Srinivasan. Revisiting Cryptographic Hardness of Finding a Nash Equilibrium. CRYPTO 2016.
- Habàcek and Yogev. Hardness of Continuous Local Search: Query Complexity and Cryptographic Lower Bounds. SODA 2016.
- Goldberg and Papadimitriou. Towards a Unified Complexity Theory of Total Functions. 2018.
- Megiddo and Papadimitriou. A Note on Total Functions, Existence Theorems and Computational Complexity. Theoretical Computer Science 1989.
- Johnson, Papadimitriou, and Yannakakis. How Easy is Local Search?. Journal of Computer System Sciences, 1988.