Suite régularisante
En mathématiques, une suite régularisante est une suite de fonctions régulières utilisées afin de donner une approximation lisse de fonctions généralisées, le plus souvent par convolution afin de lisser les discontinuités.
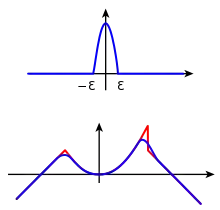
Définition
Une suite de fonctions tests (c.-à-d. C∞ à support compact) sur est dite régularisante si[1] - [2] - [3], pour tout indice :
Fonction régularisante

La façon la plus simple de construire une suite régularisante[6] est de partir d'une fonction régularisante, c.-à-d.[7] une fonction , C∞ à support compact, positive et d'intégrale 1 (sur ℝd), et de poser[8] .
Une telle fonction existe[9] - [8] : il suffit par exemple de considérer la fonction sur ℝd définie par
(où désigne la norme euclidienne) puis, en notant l'intégrale de , de poser
- .
Cette fonction régularisante est même symétrique, c.-à-d.[7] que ne dépend que de .
Propriétés
Les suites régularisantes sont principalement utilisées en théorie des distributions, afin de passer d'un problème sur des fonctions généralisées à une restriction aux fonctions régulières, plus simples à manier[9].
La convolée d'une distribution par une fonction test est une fonction de classe C∞, dont le support est inclus dans la somme de Minkowski du support de et du support de la distribution .
Soit une distribution et une suite régularisante. Alors la suite des distributions régulières associées aux fonctions converge vers dans , autrement dit : (dans ). Plus généralement[10] :
Applications
Les suites régularisantes sont utilisées pour démontrer la densité des fonctions continues dans des espaces fonctionnels plus généraux, comme les espaces Lp ou de Sobolev[12].
Elles sont également utilisées pour montrer l'équivalence des formulations faibles et fortes d'équations différentielles au sens des distributions.
Notes et références
- (en) Abdellah El Kinani et Mohamed Oudadess, Distribution Theory and Applications, World Scientific, (lire en ligne), p. 11.
- (en) Claude Gasquet et Patrick Witomski (trad. du français par R. Ryan), Fourier Analysis and Applications [« Analyse de Fourier et applications »], Springer, (lire en ligne), p. 188.
- (en) Jean-Paul Penot, Analysis : From Concepts to Applications, Springer, (lire en ligne), p. 501.
- Certains auteurs imposent , comme Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions] ou (en dimension 1) Francis Filbet, Analyse numérique, Dunod, (lire en ligne), p. 292.
- (en) Serge Lang, Real and Functional Analysis, coll. « GTM » (no 142), (1re éd. 1993) (lire en ligne), p. 227-228, appelle une suite de fonctions continues vérifiant ces trois conditions « suite de Dirac à support rétrécissant » et remarque qu'alors : .
- Certains auteurs réservent le nom de suites régularisantes à celles obtenues de cette façon, comme Lang 2012, p. 228 ou (en) Philippe Blanchard et Erwin Bruening, Mathematical Methods in Physics, Springer, (lire en ligne), p. 88.
- (en) Enrico Giusti, Minimal Surfaces and Functions of Bounded Variation, Basel, Boston, Stuttgart, Birkhäuser Verlag, coll. « Monographs in Mathematics » (no 80), , 240 p. (ISBN 978-0-8176-3153-6, zbMATH 0545.49018, lire en ligne), p. 11.
- Gilbert Demengel et Françoise Demengel, Espaces fonctionnels, EDP Sciences, (lire en ligne), p. 31-32.
- (en) Lars Hörmander, The Analysis of Linear Partial Differential Operators I, coll. « Grund. math. Wiss. » (no 256), (lire en ligne), p. 14.
- Pour une généralisation à tout groupe localement compact (au lieu de ℝd), voir (en) Zoltán Magyar, Continuous Linear Representations, North-Holland, (lire en ligne), p. 31.
- Lang 2012, p. 228 : il suffit même que soit une suite de fonctions continues positives d'intégrale 1 telle que .
- Brezis.
































