Subdivision d'un intervalle
En mathématiques, une subdivision d'un segment [a, b] de la droite réelle est une suite finie de la forme
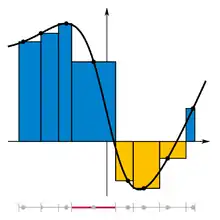
utilisation d'une subdivision d'un intervalle compact pour approcher l'intégrale d'une fonction continue
De telles subdivisions sont utilisées dans les théories de l'intégrale de Riemann, l'intégrale de Stieltjes et l'intégrale d'une fonction réglée.
Vocabulaire
- Une telle subdivision est dite adaptée à une fonction en escalier f sur [a, b] si f est constante sur chaque sous-intervalle ]xi – 1, xi[, pour i = 1, … , n.
- Un raffinement d'une subdivision P est une subdivision Q du même intervalle, formée en rajoutant des points. On dit alors que Q est plus fine que P. On définit ainsi un ordre partiel sur les subdivisions d'un intervalle.
- Le raffinement commun de deux subdivisions est la subdivision formée en prenant la réunion des deux ensembles de points et en les renumérotant par ordre croissant.
- Un marquage d'une subdivision x0 < x1 < x2 < ... < xn est la donnée supplémentaire d'un point dans chaque sous-intervalle, c'est-à-dire de points ti ∈ [xi – 1, xi], pour i = 1, … , n. À toute fonction f sur un intervalle et toute subdivision marquée de cet intervalle est associée une somme de Riemann[1].
- De même que pour les subdivisions, on définit un ordre partiel naturel sur les subdivisions marquées.
- Le pas d'une subdivision x0 < x1 < x2 < ... < xn est la plus grande des longueurs des sous-intervalles, c'est-à-dire : max{ |xi – xi – 1| : i = 1, … , n }. L'intégrale de Riemann de f est (si elle existe) la limite des sommes de Riemann quand le pas tend vers 0.
Généralisation en dimensions supérieures
Pour définir les intégrales multiples de Riemann, la généralisation en dimension n[2]…
- … d'un segment est un pavé fermé, c'est-à-dire un produit P = I1 × … × In de n segments Ij = [aj, bj] (par exemple un parallélogramme si n = 2 ou un parallélépipède si n = 3).
- Le volume de P est le produit des longueurs de ces segments : vol(P) = ∏1 ≤ j ≤ n (bj – aj).
- Le diamètre de P est le maximum de ces longueurs : δ(P) := max1 ≤ j ≤ n (bj – aj).
- L'intérieur de P est le pavé ouvert produit des intervalles ouverts bornés ]aj, bj[.
- Une subdivision de P est une famille finie u = (Pk)1 ≤ k ≤ M de pavés fermés dont les intérieurs sont disjoints et dont la réunion est égale à P. On a alors : vol(P) = ∑1 ≤ k ≤ M vol(Pk).
- Le pas de u est δ(u) := max1 ≤ k ≤ M δ(Pk).
- Un marquage de u est le choix d'un point dans chaque Pk.
- Un raffinement de u est une subdivision v = (Qℓ)1 ≤ ℓ ≤ N telle que chaque Pk soit une réunion de certains Qℓ.
Références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Partition of an interval » (voir la liste des auteurs)
, dont la référence était (en) Russell A. Gordon, The Integrals of Lebesgue, Denjoy, Perron, and Henstock (en), AMS, coll. « GSM » (no 4), , 395 p. (ISBN 978-0-8218-3805-1, lire en ligne).
- « Riemann1854, paragraphe IV », sur culturemath.ens.fr
- Jean-Pierre Ramis, André Warusfel et al., Mathématiques Tout-en-un pour la Licence 3, Dunod, (lire en ligne), p. 127-129.
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.