Statistique mathématique

Les statistiques, dans le sens populaire du terme, traitent à l'aide des mathématiques l'étude de groupe d'une population. En statistique descriptive, on se contente de décrire un échantillon à partir de grandeurs comme la moyenne, la médiane, l'écart type, la proportion, la corrélation, etc. C'est souvent la technique qui est utilisée dans les recensements.

Une régression linéaire.

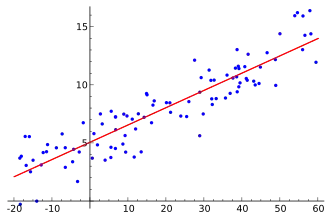
Dans un sens plus large, la théorie statistique est utilisée en recherche dans un but inférentiel. Le but de l'inférence statistique est de dégager le portrait d'une population donnée, à partir de l'image plus ou moins floue constituée à l'aide d'un échantillon issu de cette population.

Dans un autre ordre d'idées, il existe aussi la statistique « mathématique » où le défi est de trouver des estimateurs judicieux (non biaisés et efficaces). L'analyse des propriétés mathématiques de ces estimateurs sont au cœur du travail du mathématicien spécialiste de la statistique.

Statistique

La statistique mathématique repose sur la théorie des probabilités. Des notions comme la mesurabilité ou la convergence en loi y sont souvent utilisées. Mais il faut distinguer la statistique en tant que discipline et la statistique en tant que fonction des données.

Une fois les bases de la théorie des probabilités acquises, il est possible de définir une statistique à partir d'une fonction $S$ mesurable à $n$ arguments. Lorsque les valeurs $x_{1},\ldots ,x_{n}$ sont des réalisations d'une même variable aléatoire $X$ , on note :

S(X)=S(x_{1},\ldots ,x_{n})

La loi de $S(X)$ dépend uniquement de la loi de $X$ et de la forme de $S$ .

Fonctions de répartition

La fonction de répartition d'une variable aléatoire réelle $X$ (cette définition s'étend naturellement aux variables aléatoires à valeurs dans des espaces de dimension quelconque) associe à une valeur $x$ la probabilité qu'une réalisation de $X$ soit plus petite que $x$ :

F(x)={\rm {Prob}}(X\leq x)

Lorsqu'on dispose de $n$ réalisations de $X$ , on peut construire la fonction de répartition empirique de $X$ ainsi (on note $x_{(k)}$ la $k$ ^e valeur ordonnée des $x_{1},\ldots ,x_{n}$ et on pose arbitrairement $x_{0}=-\infty$ et $x_{n+1}=+\infty$ ) :

F_{n}^{*}(x)={k \over n},\,\forall x\in ]x_{(k)},x_{(k+1)}]

de même, la loi empirique peut se définir (pour tout borélien $B$ ) comme :

\mathbf {P} _{n}^{*}(B)={1 \over n}\sum _{k=1}^{n}\mathbf {1} _{x_{k}}(B)

Le théorème de Glivenko-Cantelli assure la convergence de la fonction de répartition de la loi empirique vers la fonction de répartition de la loi originale lorsque la taille $n$ de l'échantillon augmente vers l'infini.

Ces deux fonctions empiriques n'étant pas continues, on leur préfère souvent des estimateurs par noyau, qui ont les mêmes propriétés de convergence.

Types de statistiques

On définit usuellement plusieurs types de statistiques suivant la forme de $S$ :

les L-statistiques qui sont des combinaisons de statistiques d'ordres,
les M-statistiques qui s'expriment comme le maximum d'une fonction des réalisations d'une variable aléatoire,
les U-statistiques qui s'expriment sous la forme d'intégrales.

L'intérêt de cette différenciation est que chaque catégorie de statistique va avoir des caractéristiques propres.

Les estimateurs par noyau, et les moments empiriques d'une loi sont les M-statistiques.

Le moment empirique d'ordre $k$ d'une loi calculé à partir d'un échantillon $x_{1},\ldots ,x_{n}$ est :

\mu _{n}^{(k)}(X)={1 \over n}\sum _{i=1}^{n}x_{i}^{k}

Il s'agit d'un estimateur de $E(X^{k})$ . Le moment centré d'ordre $k$ est $E((X-E(X))^{k})$ . La variance est le moment centré d'ordre 2.

Exemple de statistiques : moyenne et variance

Considérons une population d'où l'on extrait un échantillon d'effectif n de façon purement aléatoire dont les éléments sont $x_{i}$ . Dans ce cas, la statistique descriptive qui estime la moyenne de la population est la moyenne empirique

m={1 \over n}\sum _{i=1}^{n}x_{i}

La statistique qui estime la dispersion autour de la moyenne est la variance empirique

s^{2}={1 \over n-1}\sum _{i=1}^{n}(x_{i}-m)^{2}

La loi de probabilité associée à cette population possède une moyenne μ et une variance σ² qui sont estimés par $m$ et $s^{2}$ . Le problème est que, si on avait choisi un autre échantillon, on aurait trouvé des valeurs différentes pour ces estimations.

Ceci conduit à considérer les éléments, la moyenne empirique et la variance empirique comme des variables aléatoires. Ces variables suivent une loi de probabilité donnée. Une fois qu'on connait ces lois de probabilité, il est possible de construire les tests statistiques voulus pour étudier les paramètres d'intérêt ( μ et σ² pour cet exemple).

Sous la condition d'indépendance entre les observations, on peut calculer la moyenne (ou espérance) et la variance de la moyenne empirique. On obtient :

E[m]=\mu \qquad \qquad V[m]=\sigma ^{2}/n

L'écart-type de la moyenne empirique vaut σ / √n. Si n devient grand, le théorème central limite enseigne que la moyenne empirique suit une loi normale caractérisée par la moyenne μ et cet écart-type. Ce résultat reste valable quelle que soit la taille de l'échantillon lorsque la loi de probabilité assignée à la population est normale. Dans ce dernier cas, particulièrement important en pratique, on montre également que (n-1) s² / σ² suit une loi de χ² à n-1 degrés de liberté.

Estimation

Ces résultats s’interprètent directement en termes d’estimation.

La moyenne empirique et la variance empirique fournissent des estimations de la moyenne et de la variance de la population.
Ces estimations sont convergentes car leurs variances tendent vers zéro lorsque la taille de l’échantillon s’accroît indéfiniment.
Elles sont non biaisées car leur limite est égale à la valeur à estimer.

Le problème d’estimation est relié aux intervalles de confiance. L’idée est de fournir une estimation d’un paramètre accompagnée d’une idée de sa précision liée aux fluctuations échantillonnales.

Voici un exemple bien spécifique d’intervalle de confiance pour la moyenne.

Pour décrire le principe, considérons un exemple assez artificiel qui présente l’avantage de la simplicité : l’estimation de la moyenne ( $m$ ) d’une population supposée normale dont nous connaîtrions l’écart-type ( $\sigma$ ). D’après le paragraphe précédent, la moyenne empirique suit également une loi normale dont l’écart-type est divisé par le facteur ${\sqrt {n}}$ .

Puisque les tables de probabilités de la loi normale sont connues, nous pouvons déterminer qu’un intervalle centré autour de la moyenne empirique aura $x$ % de chance de contenir la vraie moyenne. En pratique, $x$ est souvent fixé à 95. Lorsqu’on fixe $x$ (à 95 par exemple), on détermine la longueur de l’intervalle de confiance simplement par connaissance de la loi normale. Voici l’intervalle de confiance à 95 % pour ce cas très précis.

$[m-{{1.96\sigma } \over {\sqrt {n}}}\ ;m+{{1.96\sigma } \over {\sqrt {n}}}]$

voir aussi loi de Student.

Tests d'hypothèses

Notion générale de test d'hypothèse statistique

Une hypothèse statistique concerne les paramètres issus d'une ou plusieurs populations. On ne peut pas la vérifier mais seulement la rejeter lorsque les observations paraissent en contradiction avec elle. Nous conclurons que la valeur observée (à partir de l'échantillon) est très peu probable dans le cadre de l'hypothèse (qui concerne la population).

La première étape consiste à édicter l'hypothèse nulle. Souvent cette hypothèse sera ce qu'on croit faux.

Exemple d'hypothèses nulles :

Les deux moyennes issues de deux populations sont égales,
La corrélation entre deux variables est nulle,
Il n'y a pas de lien entre l'âge et l'acuité visuelle, etc.

L'hypothèse nulle concerne les paramètres (valeurs vraies) de la population.

Pour chaque test statistique, il y a une mesure ou statistique précise (selon le paramètre qui nous intéresse) qui suit une loi de probabilité connue. Cette statistique peut être vue comme une mesure de l'écart entre ce qu'on observe dans l'échantillon et ce qu'on postule dans la population (hypothèse nulle). Plus cette mesure sera grande, plus sa probabilité d'occurrence sera petite. Si cette probabilité d'occurrence est trop petite, on aura tendance à rejeter l'hypothèse nulle et donc conclure que l'hypothèse nulle est fausse.

Test paramétrique

Se dit des tests qui présupposent que les variables à étudier suivent une certaine loi décrite par des paramètres. De nombreux tests paramétriques concernent des variables qui suivent la loi normale. Les tests t pour échantillons indépendants ou appariés, les ANOVA, la régression multiple, le test de Wald, etc.

Test du χ²

Voici l'exemple d'un test qui utilise la loi du χ². Cependant, une multitude de tests utilisent cette loi de probabilité : Mc Nemar, tests d'adéquation de modèles, tests d'adéquation à une loi, etc.

Exemple :

On se demande si un échantillon extrait d'une population correspond raisonnablement à une loi de probabilité hypothétique.

L'échantillon d'effectif $n$ est divisé en $k$ classes d'effectifs $n_{i}$ comme pour la construction d'un histogramme, avec une différence : il est possible d'utiliser des classes de largeur variable, c'est même recommandé pour éviter qu'elles soient trop petites. Avec cette précaution, le théorème central limite dans sa version multidimensionnelle indique que le vecteur des effectifs $(n_{1},...,n_{k})$ se comporte approximativement comme un vecteur gaussien.

La loi de probabilité étant donnée d'autre part, elle permet d'assigner à chaque classe une probabilité $p_{i}$ . Dans ces conditions l'expression

\sum _{i=1}^{k}{{(n_{i}-np_{i})^{2}} \over {np_{i}}}

qui représente d'une certaine manière la distance entre les données empiriques et la loi de probabilité supposée, suit une loi de probabilité de χ² à $k-1$ degrés de liberté.

Les tables de χ² permettent de déterminer s'il y a lieu de rejeter l'hypothèse en prenant le risque, fixé à l'avance, de se tromper.

Si on considère le cas d'une loi de probabilité dont les paramètres (en général moyenne et écart-type) sont inconnus, la minimisation du χ² par rapport à ces paramètres fournit une estimation de ceux-ci.

Voir aussi

Bibliographie

Denis Bosq, Statistique mathématique et statistique des processus. Hermes/Lavoisier, 2012.
Benoît Cadre, Céline Vial, Statistique mathématique, cours et exercices corrigés, Ellipses, 2012.
Gilles Stoltz, Vincent Rivoirard, Statistique mathématique en action, Vuibert, 2012.
Jean-Pierre Favre, Mathématiques de gestion, Digilex, 2009 (ISBN 978-2-940404-01-8).
Borokov, A. A. (1999), Mathematical Statistics. Taylor & Francis (ISBN 90-5699-018-7).
Didier Pelat, Bruits et Signaux (introduction aux méthodes de traitements des données) : statistique des variables aléatoires.
P. E. Greenwood et M. S. Nikulin, A Guide to Chi-Squared Testing, John Wiley and Sons, 1996.
(en) George Casella et Roger Berger, Statistical Inference, Brooks/Cole, 2001, 2^e éd.

Articles connexes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.