Spirale d'or
En géométrie, une spirale d'or est une spirale logarithmique avec un facteur de croissance de , appelé nombre d'or[1]. Une spirale d'or devient plus large par un facteur de φ pour chaque quart de tour qu'elle fait.
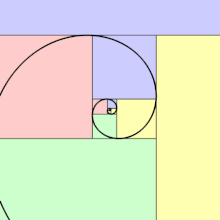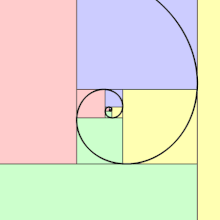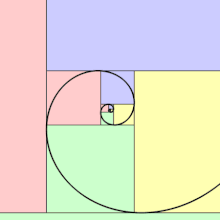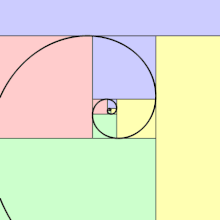
La spirale d'or est autosimilaire, elle se répète à l'infini lorsqu'elle est agrandie.

La spirale de Fibonacci (courbe verte constituée de l'ensemble de quart de cercles tangents à chaque carré) est une approximation de la spirale d'or (courbe rouge). Les parties jaunes indiquent les portions où les deux courbes se superposent. Les côtés des carrés successifs respectent la proportion d'or.
Formule
La spirale d'or est la courbe d'équation polaire suivante[2] :
ou encore :
avec e la base des logarithmes naturels, a étant une constante réelle strictement positive arbitraire et b donné par :
Voir aussi
Notes et références
(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Golden spiral » (voir la liste des auteurs).
- Chang, Yu-sung, "Golden Spiral « https://web.archive.org/web/20190728084311/http://demonstrations.wolfram.com/GoldenSpiral/ »(Archive.org • Wikiwix • Archive.is • Google • Que faire ?), ", The Wolfram Demonstrations Project.
- Priya Hemenway, Divine Proportion: Φ Phi in Art, Nature, and Science, Sterling Publishing Co, , 127–129 p. (ISBN 1-4027-3522-7)
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.



