Sphéricône
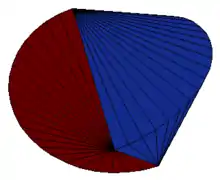
Le sphéricône est un solide formé de deux demi-cônes se raccordant continûment. Il possède deux arêtes en demi-cercles, et quatre sommets formant un carré.
Histoire
D'après Ian Stewart[1] et Paul J. Roberts[2], il a été inventé vers 1970 par Colin J. Roberts, passionné de menuiserie, qui travaillait au départ sur un ruban de Möbius. Il lui a donné son nom.
L'inventeur de jeux israélien David Haran Hirsch le redécouvrit et le fit breveter en 1980 [3], et Ian Stewart l'a popularisé en 1999 grâce à un article dans "Scientific American", traduit dans "Pour la Science"[4].
Définition
Pour le construire, prendre deux troncs de cônes de révolution d'angle droit et de sommets opposés ayant la même base, découper suivant quatre génératrices formant un carré, et faire pivoter l'une des parties de 90°.
On peut aussi le définir comme l'enveloppe convexe des deux demi-cercles orthogonaux de même centre formant ses arêtes.
Propriétés géométriques
L'aire de la surface d'un sphéricône de rayon r est donnée par
- .
Son volume vaut alors
- ,
ce qui est la moitié de celui d'une sphère de même rayon.
Propriétés
Sa particularité (contrairement à la sphère) est d'avoir une surface développable, à savoir qu'il peut rouler sans glisser sur un plan, en développant toute sa surface. La trace de ce roulement peut être découpée de sorte à le reconstituer.
Références
- Ian STEWART, Les Divagations Mathématiques de Ian Stewart, Paris, Dunod, , p. 127-135
- (en) « Sphericon : history » (consulté le )
- David Haran Hirsch (1980): "Patent no. 59720: A device for generating a meander motion; Patent drawings; Patent application form; Patent claims
- Ian Stewart, Pour la Science, n° 265, novembre 1999
Voir aussi
- L'oloïde
Liens externes
- Animation de la construction du sphéricône.
- Modèles en papier.
- Variantes à partir de polygones réguliers.
- Vidéo montrant le roulement du sphéricône sur un plan.
- Page d'Alain Esculier détaillant le cas général.

