Oloïde

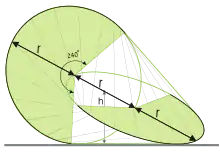
Structure de l'oloïde.

Comme le montre la figure de gauche, on considère deux cercles de même rayon r situés dans des plans perpendiculaires. Chaque cercle passe par le centre de l'autre. Ces deux cercles constituent la structure de l'oloïde.

On considère maintenant l'enveloppe convexe de ces deux cercles (traits verts). On remarque alors qu'une portion de chaque cercle se trouve à l'intérieur de l'enveloppe convexe. Cela montre que l'on aurait pu aussi définir l'oloïde comme l'enveloppe convexe d'arcs de cercle d'angle 240° chacun (dessinés sur la figure en noir).

L'oloïde est alors la surface (frontière) de cette enveloppe convexe.

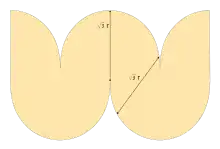
Développement de l'oloïde.

Cette surface est une partie de la surface développable s'appuyant sur deux cercles.

Cette dernière est une surface algébrique de degré 8 d'équation :

${\displaystyle 4x^{2}+4x^{3}-7x^{4}-8x^{5}+2x^{6}+4x^{7}+x^{8}+4y^{2}+4xy^{2}-18x^{2}y^{2}-16x^{3}y^{2}+}$

${\displaystyle 14x^{4}y^{2}+12x^{5}y^{2}-11y^{4}-8xy^{4}+22x^{2}y^{4}+12x^{3}y^{4}-6x^{4}y^{4}+10y^{6}+}$

${\displaystyle 4xy^{6}-8x^{2}y^{6}-3y^{8}+4xz^{2}-6x^{2}z^{2}-48x^{3}z^{2}-46x^{4}z^{2}-12x^{5}z^{2}-}$

${\displaystyle 10y^{2}z^{2}-52xy^{2}z^{2}-46x^{2}y^{2}z^{2}+12x^{3}y^{2}z^{2}+6x^{4}y^{2}z^{2}+24xy^{4}z^{2}+}$

${\displaystyle 12x^{2}y^{4}z^{2}+6y^{6}z^{2}+z^{4}-8xz^{4}-50x^{2}z^{4}-36x^{3}z^{4}-6x^{4}z^{4}-12y^{2}z^{4}+}$

${\displaystyle 12x^{2}y^{2}z^{4}-9y^{4}z^{4}-2z^{6}-20xz^{6}-8x^{2}z^{6}+6y^{2}z^{6}-3z^{8}=0}$

Le sphéricône.

• http://www.heldermann-verlag.de/jgg/jgg01_05/jgg0113.pdf

• http://www.mathcurve.com/surfaces/orthobicycle/orthobicycle.shtml

• http://www.apmep.asso.fr/IMG/pdf/atelierD20.pdf

• [vidéo] L'objet qui te retourne le cerveau... (Oloïde) sur YouTube, chaine Dr Nozman.

• [vidéo] Incredible Rolling Objects which aren't Spheres! (Oloïde) sur YouTube, chaine Maker's Muse.