Rotation de Mercure
La rotation de Mercure est un sujet d'étude important en planétologie. Bien que, à la fin du XIXe siècle, Giovanni Schiaparelli eût estimé que Mercure est en rotation synchrone et que ce résultat eût par la suite été soutenu par d'autres astronomes, les observations effectuées à partir du milieu des années 1960 ont permis de déterminer que la planète est en résonance spin-orbite 3:2, c'est-à -dire que sa période de rotation sidérale (58,65 jours) est deux tiers de sa période de révolution (87,97 jours). De ce fait, Mercure ne montre pas toujours la même face au Soleil, mais sa période de rotation solaire dure deux pleines révolutions (175,94 jours).
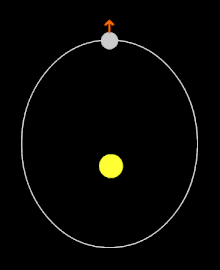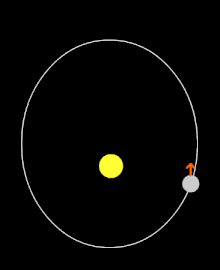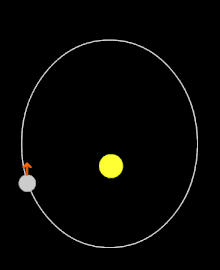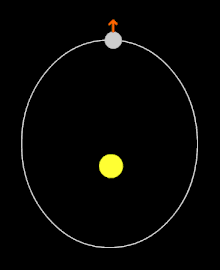
Chronologie de la détermination de la période de rotation
Début du XIXe siècle : premières estimations
Les observations optiques de Mercure ont eu lieu depuis le début du XIXe siècle. Les premières observations intensives par Johann Hieronymus Schröter furent analysées par Friedrich Wilhelm Bessel en 1813, qui annonça en avoir déduit une période de rotation proche de 24 heures.
1889-1965 : Mercure supposée en rotation synchrone
En 1889, Giovanni Schiaparelli estima, à partir de ses observations, que Mercure a une rotation lente et est très probablement en rotation synchrone, avec une période de 88 jours[1].
Eugène Antoniadi en 1934, Audouin Dollfus en 1953 et d'autres ont également estimé une période de rotation de 88 jours à partir de leurs observations.
En 1963, les premières observations radar de la planète, réalisées par Roland Carpenter et Richard Goldstein (en), semblaient compatibles avec cette période de 88 jours.
Par conséquent, les cartes de Mercure étaient réalisées à partir de l'idée que c'était sa face supposée toujours illuminée qui était cartographiée[2]. Les coordonnées à la surface de Mercure utilisaient alors comme référence 0 de longitude le méridien passant au centre de cette face.
Carte de Giovanni Schiaparelli (avant 1911).
Carte de Percival Lowell (1896).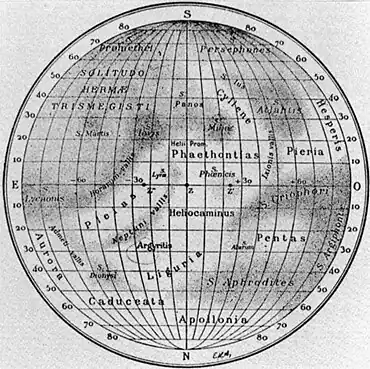
Carte d'Eugène Antoniadi (1934).
Pettengill et Dyce, 1965 : premières mesures fiables de la rotation, grâce aux observations radar
À partir du , Gordon Pettengill et Rolf Dyce, de l'université Cornell, observent Mercure avec le radiotélescope d'Arecibo[3]. Ils obtiennent alors une période de rotation de 59 ± 5 jours.
Cette mesure contredit la prédiction faite par Schiaparelli et montre que Mercure n'est pas en rotation synchrone autour du Soleil mais possiblement en résonance spin-orbite 3:2.
Govern, Gross et Rasool, 1965 : affinement de la valeur grâce aux observations visibles
En 1965, W. E. McGovern, S. H. Gross et S. I. Rasool publient un article montrant que les observations visuelles sont non seulement compatibles avec les observations radars, mais permettent en outre de déterminer une valeur plus précise de la rotation de Mercure. Ils obtiennent ainsi une période de rotation de 58,4 ± 0,4 jours[4].
Dyce, Pettengill et Shapiro, 1967
À partir d'observations radars faites en avril et , B. R. Dyce, G. H. Pettengill et Irwin I. Shapiro annoncent en 1967 une valeur de 59 ± 3 jours[5].
1970 : redéfinition des coordonnées sur Mercure
Étant donné que les nouvelles mesures ont montré que Mercure est vraisemblablement en résonance spin-orbite 3:2, l'Union astronomique internationale redéfinit, en 1970, le méridien 0° de Mercure comme étant le méridien solaire au premier périhélie après le . Ce méridien origine, de même que son opposé à 180 degrés, correspondent aux deux points chauds de Mercure, c'est-à -dire aux deux méridiens qui se retrouvent, alternativement, face au Soleil lors des périhélies de Mercure.
Goldstein, 1971
En 1971, Goldstein affina la détermination de la période de rotation de Mercure à 58,65 ± 0,25 jours en utilisant des observations radar[6].
Murray, Dollfus et Smith, 1972
J. B. Murray, Audouin Dollfus et B. Smith ont déterminé, en 1972, que l'axe de rotation de Mercure est perpendiculaire au plan de son orbite à mieux que 3 degrés et que sa période de rotation est 58,644 ± 0,009 jours, « pas significativement différente des deux tiers de la période de révolution »[7].
Mariner 10, 1974-1975
L'exploration de la planète par la sonde Mariner 10 en 1974-1975 permit de déterminer que la période de rotation de Mercure vaut 58,646 ± 0,005 jours[6].
Références
- La capture de Mercure en résonance spin-orbite 3:2 s’explique par le mouvement chaotique de son orbite, Observatoire de Paris, .
- De Mercure à Pluton, planètes et satellites, Pierre Humbert, 1937, p. 10-19
- Pettengill et Dyce 1965.
- McGovern, Gross et Rasool 1965.
- Dyce, Pettengill et Shapiro 1967.
- (en) Calvin J. Hamilton, Mercury, Institut de recherche spatiale de l'Académie des sciences de Russie, 1997.
- Murray et al. 1972.
Bibliographie
: document utilisé comme source pour la rédaction de cet article.
- [Burns 1979] (en) T. J. Burns, « On the rotation of Mercury » [« De la rotation de Mercure »], Celestial Mechanics, vol. 19,‎ , p. 297-313 (Bibcode 1979CeMec..19..297B, lire en ligne)
- [Colombo et Shapiro 1966] (en) Giuseppe Colombo et Irwin I. Shapiro, « The Rotation of the Planet Mercury » [« La rotation de la planète Mercure »], The Astrophysical Journal, vol. 145,‎ , p. 296 (Bibcode 1966ApJ...145..296C, lire en ligne)
- [Dyce, Pettengill et Shapiro 1967] (en) « Radar determination of the rotations of Venus and Mercury » [« Détermination radar des rotations de Vénus et Mercure »], The Astronomical Journal, vol. 72, no 3,‎ , p. 351 (lire en ligne).
- [Klaasen 1976] (en) Kenneth P. Klaasen, « Mercury's rotation axis and period » [« Axe et période de rotation de Mercure »], Icarus, vol. 28, no 4,‎ , p. 469-478 (DOI 10.1016/0019-1035(76)90120-2, lire en ligne)
- [Knibbe et van Westrenen 2017] (en) Jurriën Sebastiaan Knibbe et Wim van Westrenen, « On Mercury's past rotation, in light of its large craters » [« De la rotation passée de Mercure, à la lumière de ses grands cratères »], Icarus, vol. 281,‎ , p. 1-18 (DOI 10.1016/j.icarus.2016.08.036, lire en ligne)
- [Liu 1970] (en) Han-Shou Liu, « Thermal and tidal effect on the rotation of Mercury » [« Effet thermique et de marée sur la rotation de Mercure »], Celestial mechanics, vol. 2,‎ , p. 4-8 (DOI 10.1007/BF01230446, lire en ligne)
- [McGovern, Gross et Rasool 1965] (en) W. E. McGovern, S. H. Gross et S. I. Rasool, « Rotation Period of the Planet Mercury » [« Période de rotation de la planète Mercure »], Nature, vol. 208,‎ , p. 375 (DOI 10.1038/208375a0, lire en ligne).
- [Miller 1893] (en) E. Miller, « The Periods of Rotation of Mercury and Venus, and the Satellites of the Solar System » [« Les périodes de rotation de Mercure et Vénus, et les satellites du système solaire »], Transactions of the Annual Meetings of the Kansas Academy of Science, Académie des sciences du Kansas, vol. 14,‎ 1893-1894, p. 94-97 (DOI 10.2307/3623918, lire en ligne)
- [Murray, Dollfus et Smith 1972] J. B. Murray, Audouin Dollfus et B. Smith, « Cartography of the surface markings of Mercury » [« Cartographie des marquages de surface de Mercure »], Icarus, vol. 17, no 3,‎ , p. 576-584 (DOI 10.1016/0019-1035(72)90023-1, Bibcode 1972Icar...17..576M).
- [Noyelles 2014] Benoît Noyelles, « Contribution à l'étude de la rotation résonnante dans le Système Solaire », thèse d'habilitation à diriger des recherches, Université de Lille 1,‎ 2014, 230 pages (lire en ligne)Soutenue à l'Observatoire de Lille le 8 décembre 2014.
- [Peale 1976] (en) S. J. Peale, « Inferences from the dynamical history of Mercury's rotation » [« Inférences à partir de l'histoire dynamique de la rotation de Mercure »], Icarus, vol. 28, no 4,‎ , p. 459-467 (DOI 10.1016/0019-1035(76)90119-6, lire en ligne)
- [Pettengill et Dyce 1965] (en) Gordon Pettengill et Rolf Dyce, « A Radar Determination of the Rotation of the Planet Mercury » [« Une détermination radar de la rotation de la planète Mercure »], Nature, no 206,‎ , p. 1240 (lire en ligne).
- [Pfyffer 2010] (en) Gregor Pfyffer, « Libration and obliquity of Mercury from the BepiColombo radio science and camera experiments » [« Libration et obliquité de Mercure à partir des expériences de science radio et caméra de BepiColombo »], thèse de doctorat, Université catholique de Louvain,‎ (lire en ligne)Prom. : Véronique Dehant et Tim Van Hoolst.
- [Rambaux et Bois 2004] (en) N. Rambaux et E. Bois, « Theory of the Mercury's spin-orbit motion and analysis of its main librations » [« Théorie du mouvement spin-orbite de Mercure et analyse de ses principales librations »], Astronomy & Astrophysics, no 413,‎ , p. 381-393 (DOI 10.1051/0004-6361:20031446, lire en ligne)