Retour sur trace
En informatique, plus précisément en algorithmique, le retour sur trace ou retour arrière[1] (appelé aussi backtracking en anglais) est une famille d'algorithmes pour trouver des solutions à des problèmes algorithmiques, notamment de satisfaction de contraintes. Contrairement à une recherche exhaustive, un algorithme de retour sur trace construit incrémentalement des solutions candidates. Il abandonne la construction lorsqu'il ne peut compléter le candidat courant en solution valide. Il revient alors sur ses choix (d'où le nom de retour sur trace) et en prend d'autres pour construire d'autres solutions candidates.
Le retour sur trace est utilisé pour résoudre des problèmes algorithmiques difficile à résoudre, typiquement NP-complets[2].
Principe
Ces algorithmes permettent de tester systématiquement l'ensemble des affectations potentielles du problème. Ils consistent à sélectionner une variable du problème, et pour chaque affectation possible de cette variable, à tester récursivement si une solution valide peut-être construite à partir de cette affectation partielle. Si aucune solution n'est trouvée, la méthode abandonne et revient sur les affectations qui auraient été faites précédemment (d'où le nom de retour sur trace).
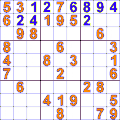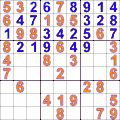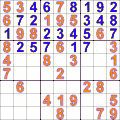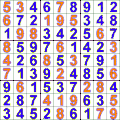 Grille de Sukodu résolue grâce au retour sur trace.
Grille de Sukodu résolue grâce au retour sur trace. Placement de huit reines sur un échiquier sans qu'elles s'attaquent.
Placement de huit reines sur un échiquier sans qu'elles s'attaquent.
La figure ci-dessus de gauche montre l'application du retour sur trace sur la recherche d'une solution pour le jeu du Sudoku. L'algorithme affecte une valeur possible dans une case puis poursuit la construction d'une solution. En cas d'impossibilité, l'algorithme revient sur les affectations déjà faites puis essait avec d'autres valeurs. La figure de droite montre l'application du retour sur trace pour le problème des huit reines. Il s'agit de placer 8 reines sur un échiquier sans qu'elles s'attaquent.
Arbre de recherche
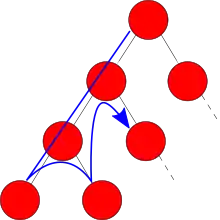
Le retour sur trace peut être vu comme un parcours en profondeur dans l'arbre de recherche du problème, aussi appelé arbre de l'espace d'état (en anglais state-space tree[2]). L'arbre de recherche du problème est construit comme suit. La racine de l'arbre est le point de départ de notre algorithme : on part de la solution vide. Les enfants d'un nœud dans l'arbre sont obtenus en étendant la solution, typiquement en affectant une variable du problème. On montre ici deux exemples d'arbres de recherche : le premier pour le problème de placer quatre reines (l'arbre de recherche pour le problème des huit reines est trop grand pour être montrer), et pour le problème de couverture exacte.
 Arbre de recherche pour essayer de placer 4 reines sur un plateau d'échecs de taille 4x4, de façon à ce qu'aucune reine n'en attaque une autre.
Arbre de recherche pour essayer de placer 4 reines sur un plateau d'échecs de taille 4x4, de façon à ce qu'aucune reine n'en attaque une autre.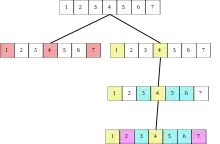 Arbre de recherche pour le problème de couverture exacte. Ici, on se demande si on peut couvrir {1, 2, 3, 4, 5, 6, 7} par une partition composée de sous-ensembles parmi {1, 4, 7}, {1, 4}, {3, 5, 6}, {4, 5, 7}, {2, 3, 6, 7}, {2, 7}.
Arbre de recherche pour le problème de couverture exacte. Ici, on se demande si on peut couvrir {1, 2, 3, 4, 5, 6, 7} par une partition composée de sous-ensembles parmi {1, 4, 7}, {1, 4}, {3, 5, 6}, {4, 5, 7}, {2, 3, 6, 7}, {2, 7}.
La pile est une structure de donnée fondamentale pour le retour sur trace, elle permet de stocker (empiler) les branchements effectués et de les mettre à jour (dépiler) lors d'un retour. L'utilisation de cette pile est exactement la façon de procéder d'un parcours en profondeur. Une des implémentations de l'algorithme utilise des appels récursifs et donc la pile d'exécution.
Pseudo-code
Il existe plusieurs pseudo-codes selon les auteurs. A chaque fois, on donne des schémas d'algorithmes, c'est-à-dire que les pseudo-codes données ici s'appliquent à de nombreux problèmes.
Version récursive
Levitin, dans son livre[2], donne une version récursive. On suppose ici qu'une solution candidate se représente avec des variables X[1..i] et que la i-ème variable X[i] est à valeurs dans Si. L'algorithme générique du backtracking s'écrit comme suit :
entrée : X[1..i] les valeurs des i premières variables d'une potentielle solution
sortie : écrit toutes les solutions dont les premières variables valent X[1..i]
fonction backtrack(X[1..i])
si X[1..i] est une solution
écrire X[1..i]
sinon
pour tout élément x dans Si+1 consistant avec X[1..i] et les contraintes du problème
X[i+1] := x
backtrack(X[1..i+1])
L'algorithme débute avec backtrack(X[1..0]) où X[1..0] est le tuple vide (c'est la racine dans un arbre de recherche).
Version itérative
Dasgupta et al., dans leur livre, eux donne une version itérative[3] et reste plus abstrait quant aux contenus des nœuds de l'arbre de recherche, qu'ils appellent sous-problèmes :
commencer avec un problème P0 (c'est la racine de l'arbre)
S := {P0} l'ensemble des sous-problèmes actifs
tant que S est non vide
choisir un sous-problème P de S
retirer P de S
développer P des sous-problèmes plus petits P1, ... Pk
pour chaque Pi
si Pi peut se voir comme une solution
s'arrêter et afficher la solution
si Pi ne peut pas être étendue en une solution
oublier Pi
sinon
ajouter Pi à S
dire qu'il n'y a pas de solution
Les parties soulignées de l'algorithme ci-dessus dépendent du problème que l'on souhaite résoudre.
Exemples
Problèmes de satisfaction de contraintes
Les problèmes de satisfaction sont des problèmes ayant une solution complète, dans laquelle aucun ordre naturel des éléments n'existe. Ces problèmes se composent d'un ensemble de variables dont les valeurs sont assujetties à des contraintes spécifiques au problème. L'idée maîtresse consiste à essayer chaque possibilité (combinaison) jusqu'à trouver la bonne. Pour cela on examine les possibilités immédiates, puis si aucun blocage n'apparaît on continue sur les possibilités suivantes ; si un blocage apparaît, autrement dit s'il n'y a aucune possibilité, on revient au dernier cas examiné où une autre possibilité existait et on continue à partir de ce cas. Les langages de programmation déclaratifs, comme Prolog, permettent d'exprimer directement ces contraintes et effectuent cette recherche automatiquement.
Jeux et casse tête
On peut, dans un jeu que l'on programme, envisager un mouvement donné et ses suites. Il se peut que l'une des suites ne soit pas heureuse. On remonte alors à un point donné et on envisage un autre mouvement.
Couverture exacte

Le problème de la couverture exacte consiste à sélectionner des sous-ensembles de façon à obtenir une partition d'un ensemble d'éléments. Ce problème est intéressant car plusieurs autres problèmes, comme des pavages, ou résoudre un Sudoku peuvent se voir comme un problème de couverture exacte. Donald Knuth a inventé l'algorithme X[4], dédié à ce problème qui est un algorithme de retour sur trace, ainsi qu'une structure de données pour représenter une solution partielle : les liens dansants.
Comparaison avec d'autres algorithmes
Le backtracking est proche des algorithmes suivants :
Notes et références
- Office québécois de la langue française, « retour arrière », sur gdt.oqlf.gouv.qc.ca, (consulté le )
- (en) Anany Levitin, Introduction To Design And Analysis Of Algorithms, Pearson, (ISBN 978-0-13-231681-1), Section 12.1 Backtracking
- (en) Dasgupta, C. H. Papadimitriou, and U. V. Vazirani, Algorithms, McGraw-Hill Higher Education, , 318 p. (ISBN 978-0073523408), p. 272
- (en) Knuth, Donald, « Dancing links », .