Relation M-sigma

La relation M-sigma, ou relation M_BH-σ, est une corrélation empirique observée entre, d'une part, la dispersion des vitesses σ mesurée dans le bulbe d'une galaxie et, d'autre part, la masse M_BH du trou noir supermassif au centre de cette galaxie. Cette relation s'écrit mathématiquement sous la forme ${\displaystyle {\begin{smallmatrix}M_{\mathrm {BH} }\ \propto \ \sigma ^{\alpha }\end{smallmatrix}}}$, dans laquelle α est un exposant empirique. On l'exprime cependant le plus souvent sous forme logarithmique par rapport à la masse solaire M_☉ : log[ M_BH / M_☉ ] = β + α × log[ σ / (200 km/s) ].

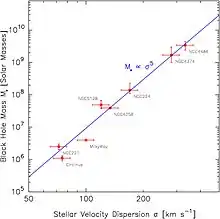
Une étude de 2009, fondée sur un échantillon de 49 valeurs publiées et 11 bornes supérieures relatives à la masse de trous noirs supermassifs dans des galaxies voisines, formule cette relation sous la forme[1] :

log[ M_BH / M_☉ ] = 8,12 ± 0,08 + ( 4,24 ± 0,41 ) × log[ σ / (200 km/s) ] pour les galaxies à disque,

log[ M_BH / M_☉ ] = 8,23 ± 0,08 + ( 3,96 ± 0,42 ) × log[ σ / (200 km/s) ] pour les galaxies elliptiques.

Cette relation a été proposée dans une conférence donnée à l'Institut d'Astrophysique de Paris en 1999[2]. L'année suivante, elle a été publiée par deux équipes indépendantes[3] - [4]. Cette découverte marqua un tournant dans la recherche relative aux trous noirs supermassifs situés au cœur des galaxies dans la mesure où elle permettait d'accéder à l'étude quantitative de ces trous noirs, même dans les galaxies trop lointaines pour en évaluer jusqu'alors la masse, et donc d'en comprendre le rôle dans la dynamique globale des galaxies, voire de procéder à l'évaluation de la masse totale des trous noirs de l'Univers[5].

L'origine de la relation M-σ serait à rechercher dans le mode de formation des bulbes galactiques, théorisé en 1998 par les britanniques Joseph Silk et Martin Rees[6] : les trous noirs supermassifs se formeraient en premier par effondrement gravitationnel des nuages moléculaires géants du centre de la galaxie, les étoiles se formant en second lieu à partir des nuages moléculaires restants en orbite autour du trou noir central, dont le rayonnement issu du disque d'accrétion stabilise les vitesses et en limite la dispersion. Le modèle de Silk et Rees prédisait une relation ${\displaystyle {\begin{smallmatrix}M_{\mathrm {BH} }\ =K\sigma ^{\alpha }\end{smallmatrix}}}$ de même forme que celle établie de nos jours, mais avec un coefficient K beaucoup trop petit[5].

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.