Rapido (jeu)
Rapido est un jeu de hasard de la Française des jeux disponible, jusqu'en , dans des cafés et des bars. Le but est de trouver 8 nombres parmi 20 dans une première grille (grille A) et simultanément un chiffre parmi quatre (grille B). Simple d'apparence et souvent gagnant aux rangs inférieurs, ce jeu représentait en 2007 le premier jeu de hasard quant au chiffre d'affaires (23,7 %) pour la Française des jeux[1] - [2]. Début 2014, la Française des jeux remplace le Rapido par un nouveau jeu aux règles assez semblables : l'Amigo[3].
Probabilités et espérance de gain
Les règles du Rapido permettent de jouer un bulletin pour 1 €. Elles autorisent également des mises supérieures, multiples de 1 €, mais cela est en fait équivalent à jouer autant de bulletins à 1 €[4].
Dans toute cette partie sur les probabilités et espérance de gain du jeu, on considère des bulletins simples à 1 €.
Tableau des gains et de leurs probabilités
Au Rapido, les bulletins perdants avec aucun bon numéro dans la grille A, ou seulement un, sont rares.
Lorsque le joueur perd, c'est, dans 3 cas sur 4, à un ou deux numéros près sur les cinq requis pour gagner au 1er rang ou au 2e rang. Le Rapido est donc un jeu qui peut donner à certains joueurs l'illusion fréquente que "j'y étais presque..." ou "je n'étais pas loin...".
En cas de gain (1 fois sur 5,5 en moyenne), dans près de 40 % des cas le joueur ne fait que récupérer sa mise, et avec une fréquence similaire il double sa mise.
| Nombre de bons numéros dans la grille A | Nombre de bons numéros dans la grille B | Gain en euro pour une mise de 1 euro | Rang des lots gagnants | Probabilité, en %[5] | Probabilité, arrondie |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0,2947 % | une chance sur 339 | |
| 0 | 1 | 0 | 0,0982 % | une chance sur 1018 | |
| 1 | 0 | 0 | 3,7723 % | une chance sur 27 | |
| 1 | 1 | 0 | 1,2574 % | une chance sur 80 | |
| 2 | 0 | 0 | 15,4037 % | une chance sur 6 | |
| 2 | 1 | 0 | 5,1346 % | une chance sur 19 | |
| 3 | 0 | 0 | 26,4063 % | une chance sur 4 | |
| 3 | 1 | 0 | 8,8021 % | une chance sur 11 | |
| 4 | 0 | 0 | 20,6299 % | une chance sur 5 | |
| 4 | 1 | 1 | 1er rang | 6,8766 % | une chance sur 15 |
| 5 | 0 | 2 | 2e rang | 7,3351 % | une chance sur 14 |
| 5 | 1 | 6 | 3e rang | 2,4450 % | une chance sur 41 |
| 6 | 0 | 10 | 4e rang | 1,1003 % | une chance sur 91 |
| 6 | 1 | 30 | 5e rang | 0,3668 % | une chance sur 273 |
| 7 | 0 | 50 | 6e rang | 0,0572 % | une chance sur 1750 |
| 7 | 1 | 150 | 7e rang | 0,0191 % | une chance sur 5249 |
| 8 | 0 | 1000 | 8e rang | 0,0006 % | une chance sur 167960 |
| 8 | 1 | 10000 | 9e rang | 0,0002 % | une chance sur 503880 |
De façon plus résumée[6] :
| Probabilité, en % | Probabilité, arrondie | |
|---|---|---|
| Bulletin perdant à 1 numéro près (4 bons numéros dans la grille A et 0 dans la grille B, ou 3 bon numéros dans la grille A et 1 dans la grille B) | 29,43 % | 1 chance sur 3 |
| Bulletin perdant à 2 numéros près (3 bons numéros dans la grille A et 0 dans la grille B, ou 2 bon numéros dans la grille A et 1 dans la grille B) | 31,54 % | 1 chance sur 3 |
| Autre bulletin perdant | 20,83 % | 1 chance sur 5 |
| Bulletin gagnant, le joueur récupère sa mise | 6,88 % | 1 chance sur 15 |
| Bulletin gagnant, le joueur double sa mise | 7,34 % | 1 chance sur 14 |
| Bulletin gagnant avec un gain supérieur | 3,99 % | 1 chance sur 25 |
Probabilités de différents événements
Pour 1 bulletin joué, la probabilité de gagner au moins l'équivalent de sa mise est d'environ 1 chance sur 5,5. Cette probabilité est indiquée au dos du bulletin de la Française des jeux.
Pour 1 bulletin joué, la probabilité d'obtenir un gain supérieur à sa mise (c'est-à-dire d'obtenir un gain d'au moins 2 € lorsqu'on a misé 1 €) est d'environ 1 chance sur 8,8[7].
Un joueur qui jouerait 10 000 bulletins aurait une probabilité...
...légèrement inférieure à 2 % de gagner une fois au 9e rang (c'est-à-dire 10 000 euros pour 1 euro)
...de l'ordre de 0,02 % de gagner deux fois au 9e rang
...de l'ordre de 0,0001 % de gagner trois fois au 9e rang[8]
...etc.
Espérance de gain
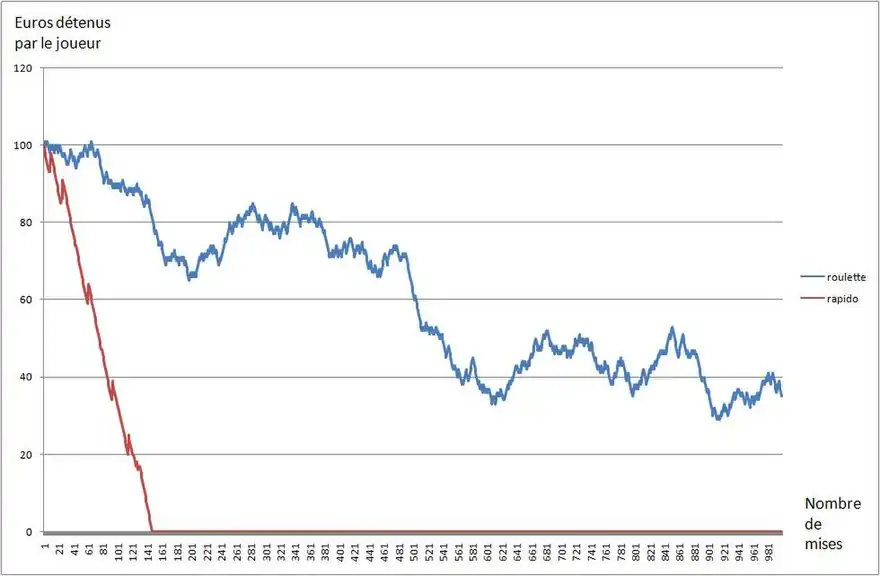
L'espérance de gain du Rapido est de -0,33€[9] pour chaque euro misé. Autrement dit, sur le long terme, les joueurs perdent en moyenne un tiers de leurs mises. On peut estimer que les pertes, lorsqu'on joue de nombreux bulletins au Rapido, sont environ 15 fois plus rapides que lorsqu'on joue à la roulette dans un casino[10] (par "rapide", on entend ici le nombre de mises qui sont jouées, comme l'illustre le graphique ci-dessous).
Exemple pour 100 € de mise au Rapido
Le graphique suivant est une simulation numérique, aléatoire, de deux joueurs jouant l'un au Rapido (courbe rouge), l'autre à la roulette en jouant systématiquement sur noir (courbe bleue). On suppose que chaque joueur joue démarre avec 100 €, joue 1 euro à chaque mise, et rejoue ses gains.
Nombre de bulletins gagnants pour cinq bulletins joués
Lorsqu'on joue souvent au Rapido, les gains sont relativement fréquents, comme le montre par exemple le tableau ci-dessous : pour seulement cinq bulletins de joués il y a environ 2 chances sur 3 que l'un des cinq bulletins au moins soit gagnant, au moins au 1er rang.
| Nombre de bulletins gagnants pour 5 bulletins joués | Probabilité en %[11] | Probabilité arrondie |
|---|---|---|
| aucun bulletin gagnant | 36,7 % | 1 chance sur 3 |
| 1 bulletin gagnant | 40,7 % | 1 chance sur 2 |
| 2 bulletins gagnants | 18,1 % | 1 chance sur 6 |
| 3 bulletins gagnants ou plus | 4,5 % | 1 chance sur 22 |
Que se passe-t-il si l'on joue beaucoup de bulletins et que l'on rejoue ses gains ?
Comme l'indique l'espérance de gain du Rapido, il est rare que le total des gains dépasse beaucoup plus que les deux tiers des mises dépensées. Pour cette raison, même s'il gagne relativement souvent, le joueur qui rejoue ses gains va voir très généralement son capital fondre rapidement.
Annexes
Notes et références
- Chiffres clés 2007 de la Française des Jeux
- Christophe Blanchard-Dignac interviewé par Laurence Girard, « « Avec le nouveau Loto, nous espérons recruter 3 millions de joueurs supplémentaires » », dans Le Monde no 19 790, 11 septembre 2008, p. 18
- avec AFP, « Le jeu de tirage Rapido sera enterré début 2014 », 20 minutes, (lire en ligne, consulté le ).
- Règles du Rapido
- La formule de calcul de la probabilité est la suivante : COMBINAISON(8;a)*COMBINAISON(12;8-a)*(b*1+(1-b)*3)/(4*COMBINAISON(20;8) ) où a est le nombre de bons numéros dans la grille A, b le nombre de bons numéros dans la grille B et COMBINAISON(n;p) vaut n!/p!(n-p)!. Voir également dans le règlement du jeu, dont la référence se trouve dans les liens externes, l'article 9 de la section 4.
- Ce deuxième tableau se déduit du premier.
- Voir dans le premier tableau la somme des probabilités des lots gagnants de rang 2 à 9, qui fait 11,32 %, soit environ 1 chance sur 8,8.
- On utilise pour ces calculs une loi binomiale de paramètres n=10000 et p=1/503880.
- Somme des produits terme à terme des gains et des probabilités, moins 1 euro.
- Pour une roulette avec 37 numéros, de 0 à 36, on a le calcul suivant : (36/37)^15 est proche de 0,67, soit 1-0,33.
- Les probabilités sont calculées par une loi binomiale de paramètres n=5 et p=1/5,5.