Protocole BB84
En cryptographie, le protocole BB84 est le premier mécanisme d'échange de clé quantique à avoir été formalisé, et en fait le premier protocole de cryptographie quantique. Il a été proposé en 1984 par Charles Bennett et Gilles Brassard[1]. Le protocole BB84 a inspiré de nombreuses variantes, qui s'appuient sur les mêmes principes fondamentaux : E90, E91, B92, SSP99, SARG04. S'il est différent du protocole d'Artur Ekert, les deux constructions sont en fait compatibles et il existe des variantes de BB84 utilisant le principe d'intrication, notamment pour résister à certaines des attaques connues.
Principe
Polarisation et mesure
Le protocole BB84 s'appuie sur la notion de polarisation linéaire d'un photon : un photon peut être émis avec une polarisation selon un axe donné. Un filtre polarisant laisse passer le photon avec une probabilité , où mesure l'écart angulaire entre l'axe de polarisation du photon et l'axe principal du filtre. Ainsi, un filtre exactement aligné avec l'axe de polarisation du photon est transparent, alors qu'un filtre formant un angle droit avec cet axe est opaque ; si l'angle est de 45° la probabilité que le photon passe le filtre est de 50 %. Si cela se produit, l'effondrement du paquet d'ondes garantit que le photon est désormais aligné avec l'axe du filtre, indépendamment de sa polarisation précédente.
On définit alors deux bases, notées et , cette dernière correspondant à une rotation de la première par 45°. Mathématiquement, on peut fixer :
Supposons un photon émis selon , et un filtre aligné selon , alors la probabilité de mesurer le photon est :
et après la mesure le photon (s'il n'a pas été absorbé) est polarisé selon .
Déroulement du protocole
Le protocole BB84 se déroule en plusieurs étapes, et permet à deux participants Alice et Bob d'établir une clé cryptographique commune. On suppose un canal de communication établi, sur lequel il est possible d'émettre des photons de polarisation choisie, les référentiels d'Alice et de Bob ayant été étalonnés préalablement.
En première étape, Alice choisit une suite aléatoire de bits ; pour chaque bit , elle choisit aléatoirement une base et émet un photon polarisé selon . De son côté, Bob choisit une base de réception aléatoire pour chaque photon, et aligne son filtre sur . L'illustration suivante donne à voir cette première étape en action :
Bit d'Alice () 0 1 1 0 1 0 0 1 Base d'Alice () Polarisation du photon () Base de Bob () Photon reçu par Bob ou ou ou ou
En deuxième étape, Bob transmet à Alice la liste des bases utilisées lors de la réception. Alice répond en indiquant quelles sont les bases que Bob a correctement choisi, et seuls les photons correspondants sont conservés[2]. Dans l'exemple ci-dessus, cela correspond à la séquence , , , , c'est-à-dire aux bits 0, 1, 0, 1. Cette séquence est appelée la clé « réconciliée » ou « trouée ».
Bit d'Alice () 0 jeté 1 jeté jeté 0 jeté 1 Base d'Alice () Polarisation du photon () Base de Bob () Photon reçu par Bob jeté jeté jeté jeté
En troisième étape, Alice et Bob se mettent d'accord sur un sous-ensemble de la clé réconciliée qu'ils vont révéler publiquement. Ils comparent alors s'ils ont obtenu les mêmes bits dans ce sous-ensemble : si oui, ils utilisent le reste de la clé pour dériver une clé cryptographique. S'il y a un désaccord, cela peut signifier un problème de transmission ou une tentative d'écoute le long du canal. En effet, le théorème de non clonage garantit qu'en cas d'écoute, l'espion force le photon sur une base (qui n'est pas forcément celle d'Alice). Ainsi, si l'espion devine correctement la base d'Alice avec une probabilité de 50 %, alors 25 % des bits de la clé de réconciliation seront en désaccord[3]. De manière générale, en sacrifiant bits de la clé de réconciliation, Alice et Bob peuvent détecter un éventuel espion sur le canal avec une probabilité .
Ainsi, en construisant une longue clé de réconciliation, on peut atteindre un niveau de sécurité suffisant en sacrifiant assez de bits[4] - [5].
Sécurité
Propriétés de sécurité
La sécurité du protocole BB84 repose sur le théorème de non clonage, qui n'est pas une hypothèse calculatoire, mais physique[6]. Sous cette hypothèse, et en supposant un équipement parfait, le protocole BB84 est sûr au sens de la théorie de l'information, c'est-à-dire qu'il garantit la sécurité même contre un adversaire disposant de capacités de calcul infinies. Cependant, comme tout protocole d'échange de clé, il est possible de monter une attaque de l'homme du milieu contre ce protocole si la communication n'est pas authentifiée. Il est donc nécessaire en pratique de complémenter le protocole BB84 d'un protocole d'authentification, classique ou quantique.
Attaque PNS et manipulations de canal
En réalité, l'équipement n'est pas parfait. Une conséquence est l'existence d'attaques sur le protocole en dépit d'une garantie théorique de sécurité.
Une de ces attaques repose sur la difficulté de produire des photons uniques : les équipements réels peuvent émettre plusieurs photons au lieu d'un seul, qu'un adversaire peut prélever du canal. Ce prélèvement est indétectable, et permet à l'adversaire de cloner des photons, violant ainsi l'hypothèse de sécurité : cette attaque est baptisée PNS (pour l'anglais photon number splitting)[7]. De nombreuses variantes de BB84 ont été imaginées pour contourner cette vulnérabilité, et il est possible en théorie d'établir une clé sûre en dépit de l'attaque[8].
Dans le protocole BB84, environ 50 % des photons transmis sont jetés lors de la réconciliation si le canal est sans erreurs[9]. Si le taux d'erreur sur le canal est trop élevé, au-delà de 11%[9], il n'est plus possible d'établir une clé. Le taux de transmission des fibres n'étant pas 100 %, et la transparence des éléments optiques n'étant pas parfaite, il est en pratique nécessaire d'augmenter l'intensité du faisceau en transmettant davantage de photons, ce qui expose les systèmes réels à l'attaque PNS même quand le nombre de photons produit est contrôlé très précisément.
D'autres attaques sont connues, reposant sur l'existence de canaux auxiliaires loin des appareils de mesure[10], sur la manipulation de phase[11], sur les décalages temporels[12], ou sur l'insertion de faux états[13], et certaines ont été montrées contre des implémentations commerciales[14].
Amplification
Une autre conséquence de l'imperfection des instruments est la présence de mesures incorrectes, même en l'absence d'espion sur le canal. Le protocole ne peut donc pas fonctionner si un désaccord se produit lors de la phase de réconciliation. Plutôt que d'accepter une session dans laquelle des erreurs sont détectées (qui peuvent être dues au bruit, à un espion, ou aux deux), il existe des techniques, dites « d'amplification » qui permettent de faire fonctionner le protocole en dépit d'erreurs mais sans avantager l'adversaire. Un exemple est l'utilisation d'un code correcteur pour décider les bits à transmettre. Il est également possible, lors de la phase de réconciliation, de ne pas transmettre les bits de la clé mais une fonction (par exemple le ou exclusif) qui ne renseigne pas l'adversaire sur la valeur ou la validité d'un bit donné[4].
Implémentation
Le protocole BB84 est aujourd'hui utilisé pour la plupart des implémentations de distribution quantique de clés. En 2007, le NIST annonçait une réalisation sur une fibre optique de 148,7 km[15]. Le protocole BB84 est supporté sur plusieurs réseaux, notamment : DARPA QKD[16], SECOCQ QKD[17], Tokyo QKD[18].
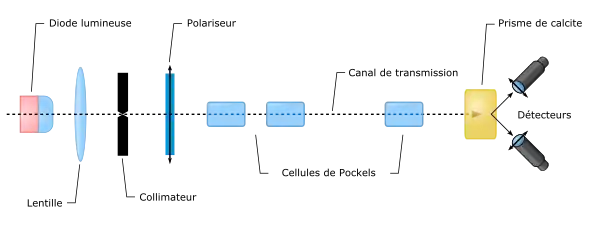
Une implémentation schématique à base de photons est illustrée ci-dessous. La source de l'émetteur produit un signal polarisé, et des cellules de Pockels sont utilisées pour commander la polarisation du signal émis. Ces cellules, commandées électriquement, permettent ainsi de produire les différents états de polarisation souhaités. Une fibre optique peut alors être utilisée pour transporter les photons. Du côté du destinataire, une cellule de Pockels peut effectuer une rotation de 45° de l'angle de polarisation, et un prisme biréfringent sépare le faisceau en deux signaux, qui sont capturés par des détecteurs à polarisation orthogonale[19].
Notes et références
- (en) Charles H. Bennett et Gilles Brassard, « Quantum cryptography: Public key distribution and coin tossing », Theoretical Computer Science, vol. 560, , p. 7–11 (DOI 10.1016/j.tcs.2014.05.025, lire en ligne, consulté le )
- Cette communication peut se faire sur un canal classique, non sécurisé.
- (en) Eleanor Rieffel et Wolfgang Polak, « An introduction to quantum computing for non-physicists », ACM Computing Surveys (CSUR), vol. 32, no 3, , p. 300–335 (ISSN 0360-0300, DOI 10.1145/367701.367709, lire en ligne, consulté le )
- (en) Nicolas Gisin, Grégoire Ribordy, Wolfgang Tittel et Hugo Zbinden, « Quantum cryptography », Reviews of Modern Physics, vol. 74, no 1, , p. 145–195 (DOI 10.1103/RevModPhys.74.145, lire en ligne, consulté le )
- (en) Samuel J. Lomonaco, « A Quick Glance at Quantum Cryptography », Cryptologia, vol. 23, , p. 1-41 (DOI 10.1080/0161-119991887739)
- (en) Dagmar Bruss, Gábor Erdélyi, Tim Meyer et Tobias Riege, « Quantum cryptography: A survey », ACM Computing Surveys (CSUR), vol. 39, no 2, , p. 6 (ISSN 0360-0300, DOI 10.1145/1242471.1242474, lire en ligne, consulté le )
- (en) Gilles Brassard, Norbert Lütkenhaus, Tal Mor et Barry C. Sanders, « Limitations on Practical Quantum Cryptography », Physical Review Letters, vol. 85, no 6, , p. 1330–1333 (DOI 10.1103/PhysRevLett.85.1330, lire en ligne, consulté le )
- (en) Daniel Gottesman, Hoi-Kwong Lo, Norbert Lütkenhaus et John Preskill, « Security of quantum key distribution with imperfect devices », Quantum Information & Computation, vol. 4, no 5, , p. 325–360 (ISSN 1533-7146, lire en ligne, consulté le )
- (en) Stephen Wiesner, « Conjugate coding », ACM SIGACT News, vol. 15, no 1, , p. 78–88 (ISSN 0163-5700, DOI 10.1145/1008908.1008920, lire en ligne, consulté le )
- (en) Sebastian Nauerth, Martin Fürst, Tobias Schmitt-Manderbach et Henning Weier, « Information leakage via side channels in freespace BB84 quantum cryptography », New Journal of Physics, vol. 11, no 6, , p. 065001 (ISSN 1367-2630, DOI 10.1088/1367-2630/11/6/065001, lire en ligne, consulté le )
- (en) Chi-Hang Fred Fung, Bing Qi, Kiyoshi Tamaki et Hoi-Kwong Lo, « Phase-Remapping Attack in Practical Quantum Key Distribution Systems », Physical Review A, vol. 75, no 3, (ISSN 1050-2947 et 1094-1622, DOI 10.1103/PhysRevA.75.032314, lire en ligne, consulté le )
- (en) Yi Zhao, Chi-Hang Fred Fung, Bing Qi et Christine Chen, « Quantum hacking: Experimental demonstration of time-shift attack against practical quantum-key-distribution systems », Physical Review A, vol. 78, no 4, , p. 042333 (DOI 10.1103/PhysRevA.78.042333, lire en ligne, consulté le )
- (en) A. Vakhitov, V. Makarov et D. R. Hjelme, « Large pulse attack as a method of conventional optical eavesdropping in quantum cryptography », Journal of Modern Optics, vol. 48, Issue 13, , p.2023-2038
- (en) Ilja Gerhardt, Qin Liu, Antía Lamas-Linares et Johannes Skaar, « Full-field implementation of a perfect eavesdropper on a quantum cryptography system », Nature Communications, vol. 2, , p. 349 (DOI 10.1038/ncomms1348, lire en ligne, consulté le )
- (en) P. A. Hiskett, D. Rosenberg, C. G. Peterson et R. J. Hughes, « Long-distance quantum key distribution in optical fibre », New Journal of Physics, vol. 8, no 9, , p. 193 (ISSN 1367-2630, DOI 10.1088/1367-2630/8/9/193, lire en ligne, consulté le )
- (en) Chip Elliott, Alexander Colvin, David Pearson et Oleksiy Pikalo, « Current status of the DARPA Quantum Network », arXiv:quant-ph/0503058, (lire en ligne, consulté le )
- (en) M. Peev, C. Pacher, R. Alléaume et C. Barreiro, « The SECOQC quantum key distribution network in Vienna », New Journal of Physics, vol. 11, no 7, , p. 075001 (ISSN 1367-2630, DOI 10.1088/1367-2630/11/7/075001, lire en ligne, consulté le )
- (en) M. Sasaki, M. Fujiwara, H. Ishizuka et W. Klaus, « Field test of quantum key distribution in the Tokyo QKD Network », Optics Express, vol. 19, no 11, , p. 10387–10409 (ISSN 1094-4087, DOI 10.1364/oe.19.010387, lire en ligne, consulté le )
- (en) Anthony Mark Fox, Quantum optics : an introduction, Oxford University Press, , 378 p. (ISBN 978-0-19-856672-4, OCLC 181099168, lire en ligne), p. 250






















