Problème de satisfiabilité de circuit

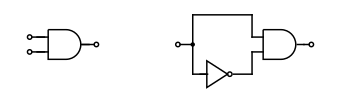
En informatique théorique, le problème de satisfaisabilité d'un circuit (aussi connu sous le nom de CIRCUIT-SAT, CircuitSAT, CSAT, etc.) est le problème de décision consistant à déterminer si pour un circuit booléen donné, il existe une affectation de ses entrées qui rende la sortie vraie[1]. En d'autres termes, on demande si les entrées d'un circuit booléen donné peuvent être réglées de manière cohérente sur 1 ou 0 de sorte que le circuit émette 1. Si tel est le cas, le circuit est dit satisfaisable. Sinon, le circuit est dit insatisfaisable. Sur la figure de droite, le circuit de gauche peut être satisfait en définissant les deux entrées sur 1, mais le circuit de droite n'est pas satisfaisable.

Le circuit de gauche est satisfaisable mais pas le circuit de droite.

CIRCUIT-SAT est étroitement lié au problème de satisfiabilité booléenne (SAT) et est NP-complet[2] comme lui. Le théorème de Cook-Levin est parfois prouvé sur CIRCUIT-SAT plutôt que sur SAT, puis réduit aux autres problèmes de satisfiabilité pour prouver leur NP-complétude[1] - [3]. La satisfaisabilité d'un circuit contenant $m$ portes binaires quelconques peut être décidée en temps $O(2^{0.4058m})$ [4].

Preuve de la NP-complétude

Étant donné un circuit et un ensemble d'entrées satisfaisant, on peut calculer la sortie de chaque porte en temps constant. Par conséquent, la sortie du circuit est vérifiable en temps polynomial. Ainsi, CIRCUIT-SAT appartient à la classe de complexité NP. Pour montrer qu'il est NP-difficile, il est possible de construire une réduction de 3SAT à CIRCUIT-SAT.

Supposons que la formule 3SAT d'origine ait des variables $x_{1},x_{2},\dots ,x_{n}$ , et des opérateurs (ET, OU, NON) $y_{1},y_{2},\dots ,y_{k}$ . Concevons un circuit de manière qu'il ait une entrée correspondant à chaque variable et une porte correspondant à chaque opérateur. Connectons les portes selon la formule 3SAT. Par exemple, si la formule 3SAT est $(\lnot x_{1}\land x_{2})\lor x_{3},$ le circuit aura 3 entrées, une porte ET, une porte OU et une porte NON. L'entrée correspondant à $x_{1}$ sera inversée avant l'envoi à une porte ET avec $x_{2},$ et la sortie de la porte ET sera envoyée à une porte OU avec $x_{3}.$

Notons que la formule 3SAT est équivalente au circuit conçu ci-dessus, et donc que leur sortie est la même pour des entrées identiques. Par conséquent, si la formule 3SAT a une affectation satisfaisante, le circuit correspondant émettra 1, et vice versa. Donc la réduction est correcte, et CIRCUIT-SAT est NP-dur.

Ceci complète la preuve que le problème CIRCUIT-SAT est NP-Complet.

Variantes restreintes et problèmes associés

Circuit planaire SAT

Supposons que l'on nous donne un circuit booléen planaire (c'est-à-dire un circuit booléen dont le graphe sous-jacent est planaire) contenant uniquement des portes NON-ET avec exactement deux entrées. Circuit planaire SAT est le problème de décision qui détermine si ce circuit a une affectation de ses entrées qui rende la sortie vraie. Ce problème est NP-complet[5]. En fait, si les restrictions sont modifiées de sorte qu'une porte du circuit soit une porte NON-OU, le problème qui en résulte reste NP-complet.

Circuit UNSAT

Circuit UNSAT est le problème de décision consistant à déterminer si un circuit booléen donné produit des sorties fausses pour toutes les affectations possibles de ses entrées. C'est le complément du problème Circuit SAT, et est donc co-NP-Complet .

Réduction de Circuit-SAT

La réduction de Circuit-SAT ou de ses variantes peut être utilisée pour montrer la dureté NP de certains problèmes et nous offre une alternative aux réductions à double rail et à logique binaire. Les gadgets qu'une telle réduction doit construire sont:

Un gadget filaire. Ce gadget simule les fils du circuit.
Un gadget divisé. Ce gadget garantit que tous les fils de sortie ont la même valeur que le fil d'entrée.
Des gadgets simulant les portes du circuit.
Un Vrai gadget de terminaison. Ce gadget est utilisé pour forcer la sortie de l'ensemble du circuit à être Vraie.
Un gadget tournant. Ce gadget nous permet de rediriger les fils dans la bonne direction selon les besoins.
Un gadget de croisement. Ce gadget nous permet de faire croiser deux fils sans interagir.

Problème d'inférence du démineur

Ce problème demande s'il est possible de localiser toutes les bombes sur un plateau du jeu Démineur. Il a été prouvé qu'il était Co-NP-Complet via une réduction du problème Circuit UNSAT[6]. Les gadgets conçus pour cette réduction sont les suivants: filaire, divisé, portes ET et OU et terminaison[7]. Il y a trois observations cruciales concernant ces gadgets. Tout d'abord, le gadget fractionné peut également être utilisé comme gadget NON et comme gadget tournant. Ensuite, la construction de gadgets ET et NON est suffisante, car ensemble, ils peuvent simuler la porte NON-ET universelle. Enfin, comme nous pouvons simuler le OU exclusif avec trois NON-ET, et comme le OU exclusif est suffisant pour créer un croisement, cela nous donne le gadget de croisement nécessaire.

La transformation de Tseytin

La transformation de Tseytin est une réduction de CIRCUIT-SAT à SAT. La transformation est facile à décrire si le circuit est entièrement construit à partir de portes NON-ET à 2 entrées (un ensemble fonctionnellement complet d'opérateurs booléens) : affectons à chaque réseau du circuit une variable, puis pour chaque porte NON-ET, construisons la forme normale conjonctive avec les clauses (x₁ ∨ x₃ ) ∧ (x₂ ∨ x₃ ) ∧ (¬x₁ ∨ ¬x₂ ∨ ¬x₃ ), où x₁ et x₂ sont les entrées de la porte NON-ET et x₃ est la sortie. Ces clauses décrivent complètement la relation entre les trois variables. La jonction des clauses de toutes les portes avec une clause supplémentaire contraignant la variable de sortie du circuit à être vraie complète la réduction; une affectation des variables satisfaisant toutes les contraintes existe si et seulement si le circuit d'origine est satisfiable, et toute solution est une solution au problème d'origine de trouver des entrées qui font du circuit la sortie 1[1] - [8]. L'inverse - que SAT est réductible en Circuit-SAT - suit trivialement en réécrivant la formule booléenne comme un circuit et en la résolvant.

Références

David Mix Barrington and Alexis Maciel, « Lecture 7: NP-Complete Problems », 5 juillet 2000
Luca Trevisan, « Notes for Lecture 23: NP-completeness of Circuit-SAT », 29 novembre 2001
See also, for example, the informal proof given in Scott Aaronson's lecture notes from his course Quantum Computing Since Democritus.
Sergey Nurk, « An O(2^{0.4058m}) upper bound for Circuit SAT », 1^er décembre 2009
« Algorithmic Lower Bounds: Fun With Hardness Proofs at MIT »
(en) Scott, Stege et van Rooij, « Minesweeper May Not Be NP-Complete but Is Hard Nonetheless », The Mathematical Intelligencer, vol. 33, n^o 4,‎ 1^er décembre 2011, p. 5–17 (ISSN 1866-7414, DOI 10.1007/s00283-011-9256-x)
Richard Kaye, Minesweeper is NP-complete (lire en ligne)
(en) Marques-Silva, João P. and Luís Guerra e Silva, « Algorithms for Satisfiability in Combinational Circuits Based on Backtrack Search and Recursive Learning » [PDF], 1999 (consulté le 5 avril 2021)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.